Inferenzstatistik mit Simulationstechniken
Einführung
Sebastian Sauer
Dozententage 2020
Agenda
1. Wozu Simulationstechniken?
2. Der Biertest -- Konfidenzintervall
3. Der Pringels-Test -- Hypothesen testen, Teil 1
4. Die Lächelstudie -- Hypothesen testen, Teil 2
5. Fazit
1 Wozu Simulationstechniken?
Simu ... was?
Simulationstechniken in der Datenanalyse nutzen die Stichprobendaten, um inferenzstatistische Schlüsse zu ziehen.
Didaktiver Nutzen:
A) weniger abstrakt
B) EIN Verfahren für (fast) alle Situationen
Inhaltlicher Nutzen
A) Manchmal präziser
B) Manchmal gibt es keine andere Möglichkeit
Verteilungsbasiert vs. simulationsbasiert
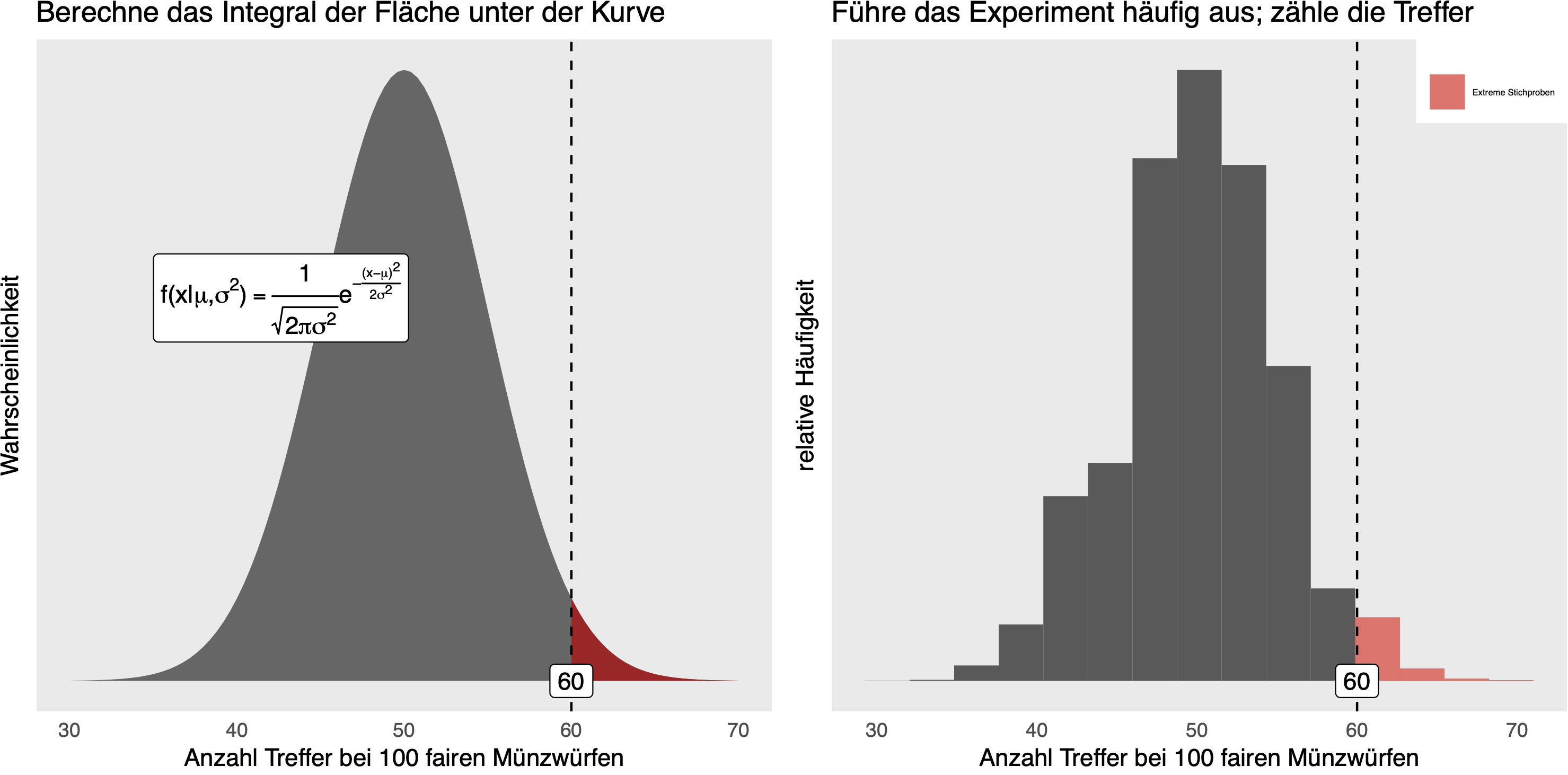
Verteilungsannahmen
... können falsch sein
Rousselet, G. A., Pernet, C. R., & Wilcox, R. R. (2019). A practical introduction to the bootstrap: A versatile method to make inferences by using data-driven simulations [Preprint]. PsyArXiv. https://doi.org/10.31234/osf.io/h8ft7
Der t-Test bei schiefen Verteilungen (I/II)
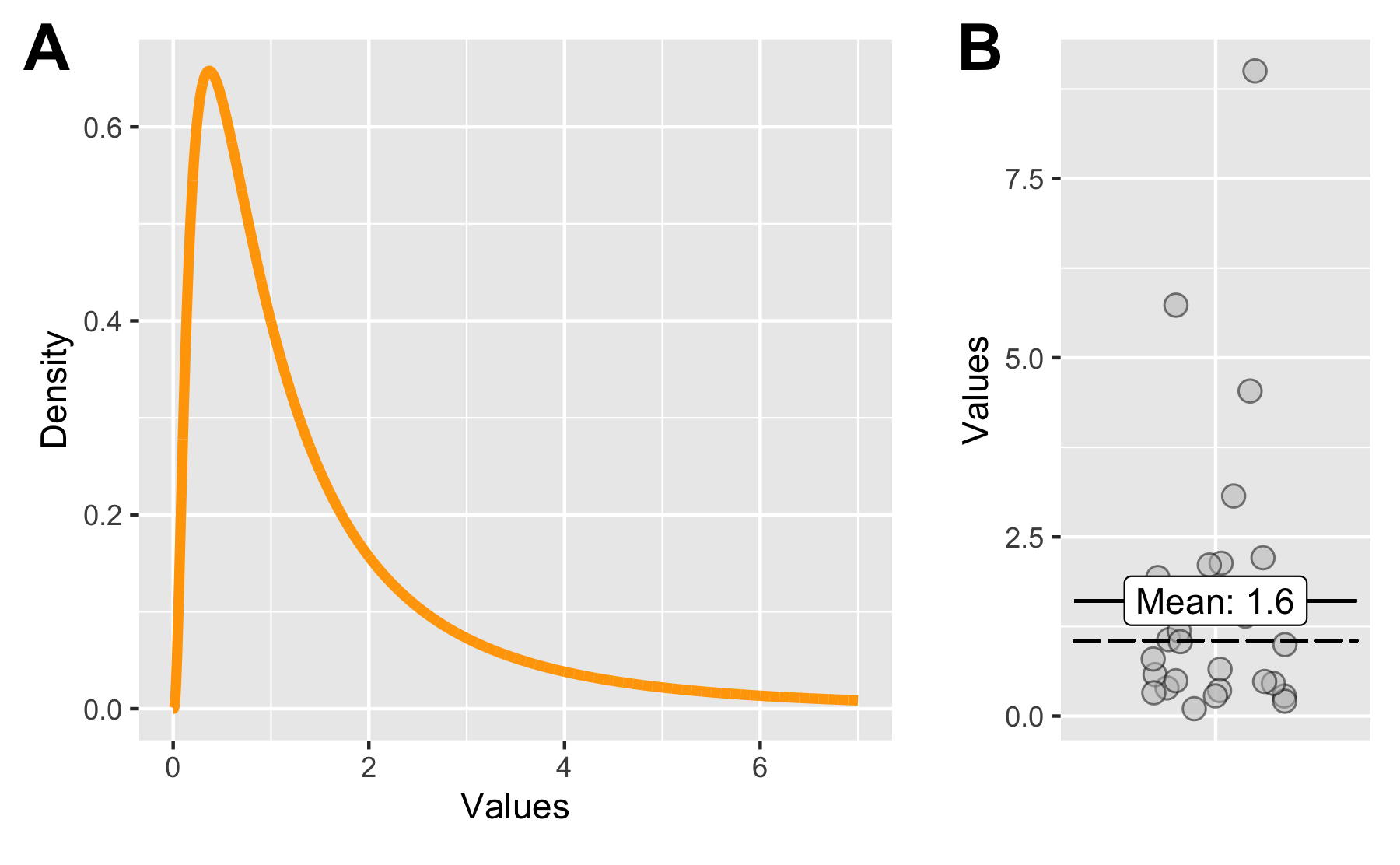
95%-KI auf Basis der der t-Verteilung mit 29 df:
#> [1] 0.9037929 2.3149338#> attr(,"conf.level")#> [1] 0.95Der t-Test bei schiefen Verteilungen (II/II)
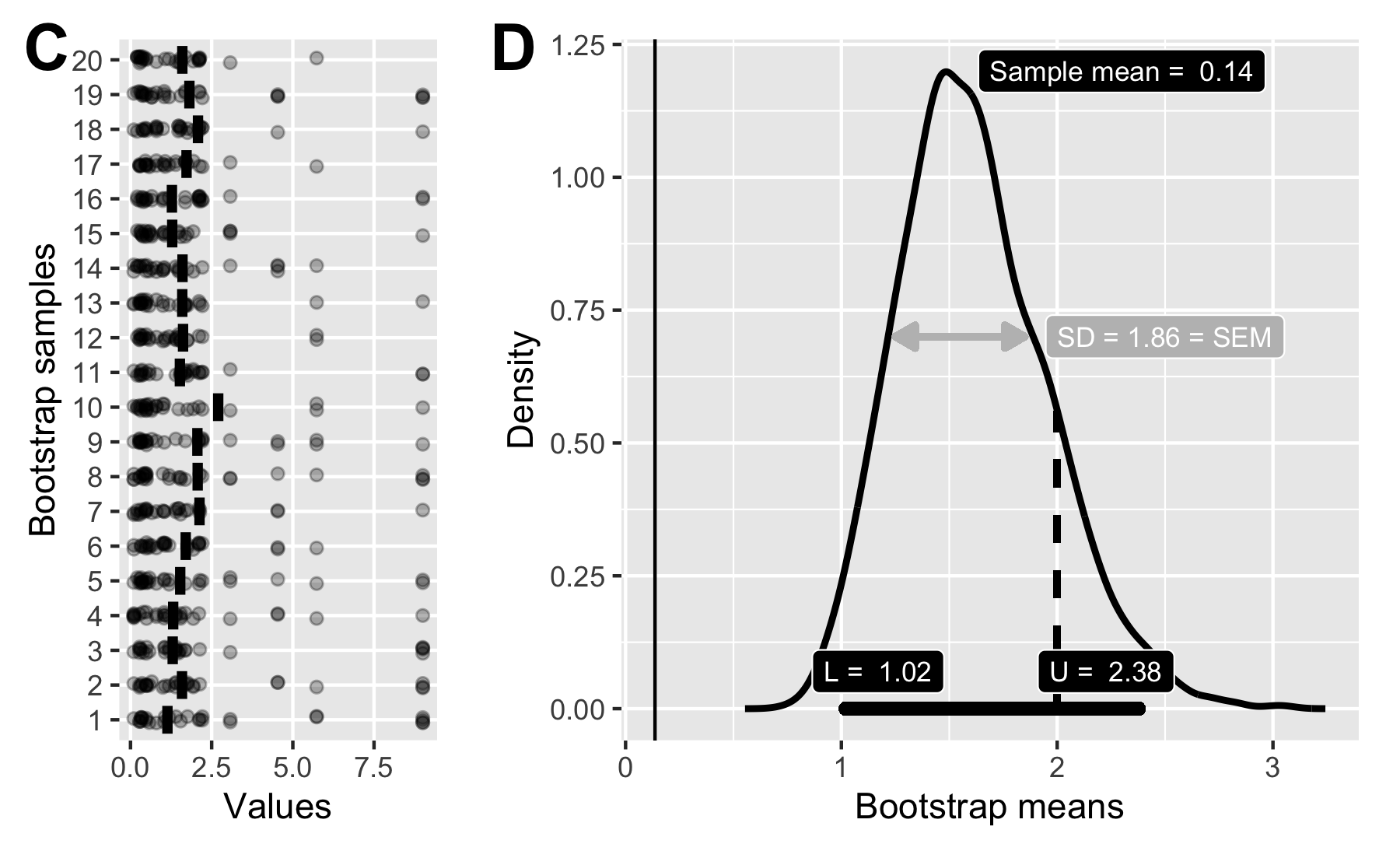
Rousselet, G. A., Pernet, C. R., & Wilcox, R. R. (2019). A practical introduction to the bootstrap: A versatile method to make inferences by using data-driven simulations [Preprint]. PsyArXiv. https://doi.org/10.31234/osf.io/h8ft7
Simulationstechniken sind nicht per se robuster
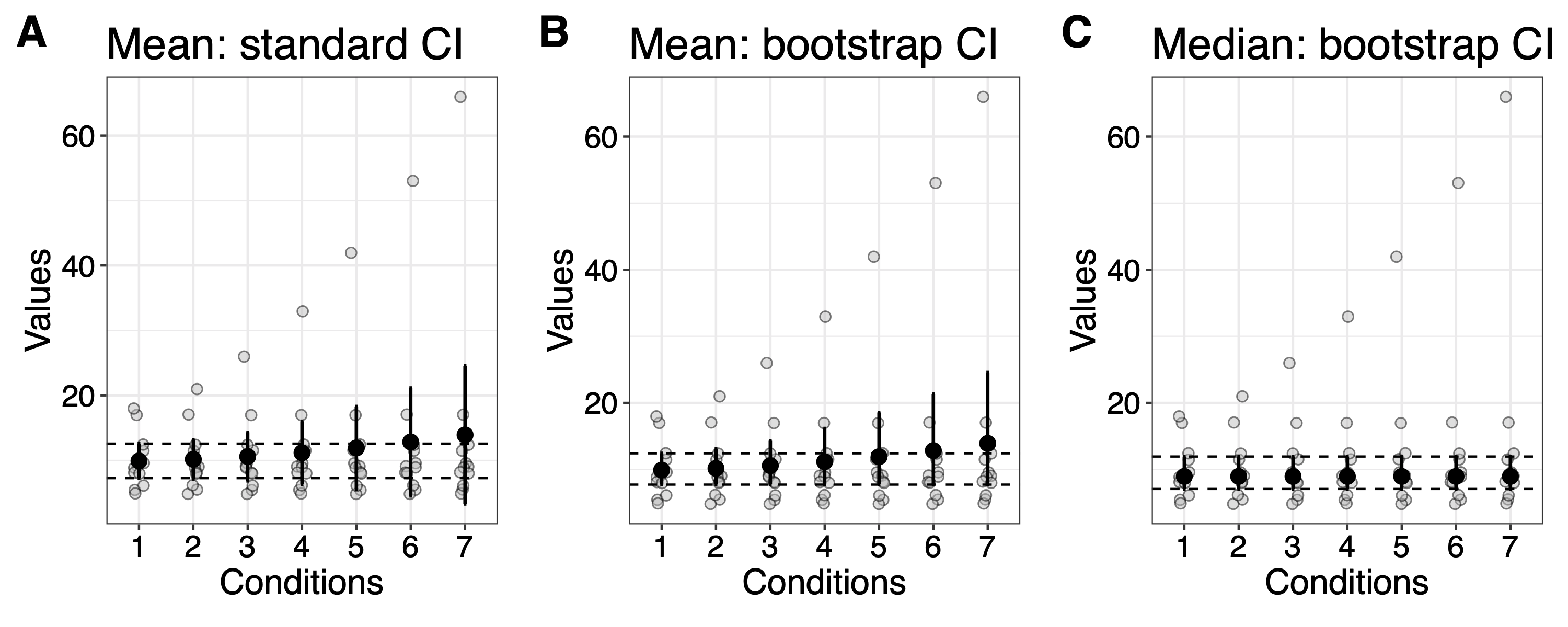
Rousselet, G. A., Pernet, C. R., & Wilcox, R. R. (2019). A practical introduction to the bootstrap: A versatile method to make inferences by using data-driven simulations [Preprint]. PsyArXiv. https://doi.org/10.31234/osf.io/h8ft7
Repro-Krise?
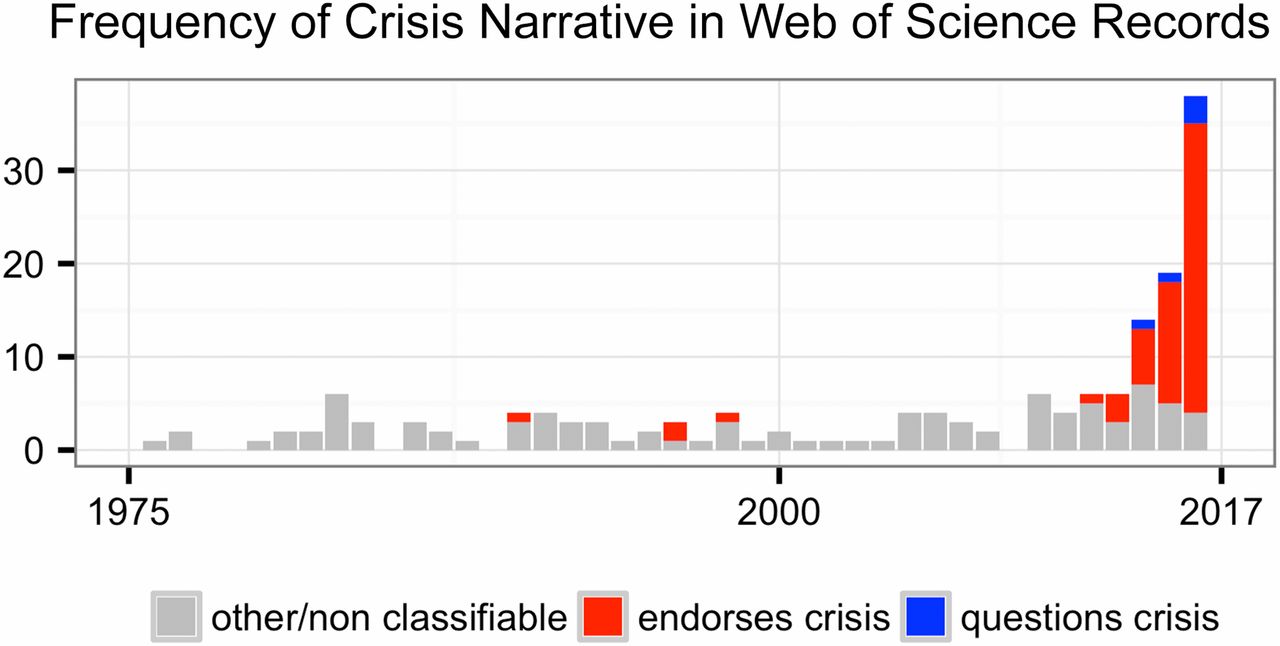
Fanelli, D. (2018). Opinion: Is science really facing a reproducibility crisis, and do we need it to? Proceedings of the National Academy of Sciences, 115(11), 2628–2631. https://doi.org/10.1073/pnas.1708272114
The Introductory Statistics Course: A Ptolemaic Curriculum?
What we teach is largely the technical machinery of numerical approximations based on the normal distribution and its many subsidiary cogs. This machinery was once necessary, because the conceptually simpler alternative based on permutations was computationally beyond our reach. Before computers statisticians had no choice. These days we have no excuse. Randomization-based inference makes a direct connection between data production and the logic of inference that deserves to be at the core of every introductory course. Technology allows us to do more with less: more ideas, less technique.
Cobb, G. W. (2007). The introductory statistics course: A Ptolemaic curriculum? Technology Innovations in Statistics Education, 1(1).
Teach statistical thinking
Emphasize Statistical Thinking
More Data and Concepts, Less Theory and Fewer Recipes
Almost any course in statistics can be improved by more emphasis on data and concepts, and less emphasis on theory and recipes.
GAISE College Report ASA Revision Committee, “Guidelines for Assessment and Instruction in Statistics Education College Report 2016,” http://www.amstat.org/education/gaise.
2 Der Biertest -- Konfidenzintervall
Live-Experiment: Biersorte erschmecken
Erschmecke das "Biligbier"
Du hast die Wahl

Im Rahmen des normalen Unterrichts einer Sonderveranstaltung der FOM wurde der Versuch durchgeführt:
- \(n=34\) Versuchspersonen*
- \(x=12\) Treffer
* Selbstloser Einsatz für die Wissenschaft
OK, kein Bier, nur Pringels
Ablauf: Schmeck den Pringel heraus!
Je zwei Personen, \(A\) und \(B\) finden sich in Pärchen
\(A\) wählt 1 Pringel-Chip und 2 Noname-Chips
\(A\) reicht \(B\) nacheinander die 3 Chips in zufälliger Reihenfolge, \(B\) hat dabei die Augen geschlossen
\(B\) entscheidet sich, welcher Chips vermutlich der Pringle-Chip ist
Das Ergebnis (Treffer ja/nein) kann hier eingetragen werden: https://forms.gle/w1bUMGvdDofadih68
Bitte notieren Sie das Ergebnis (Treffer ja/nein) auch auf einen Zettel (den zusammenfalten)
Barcode zum Link:

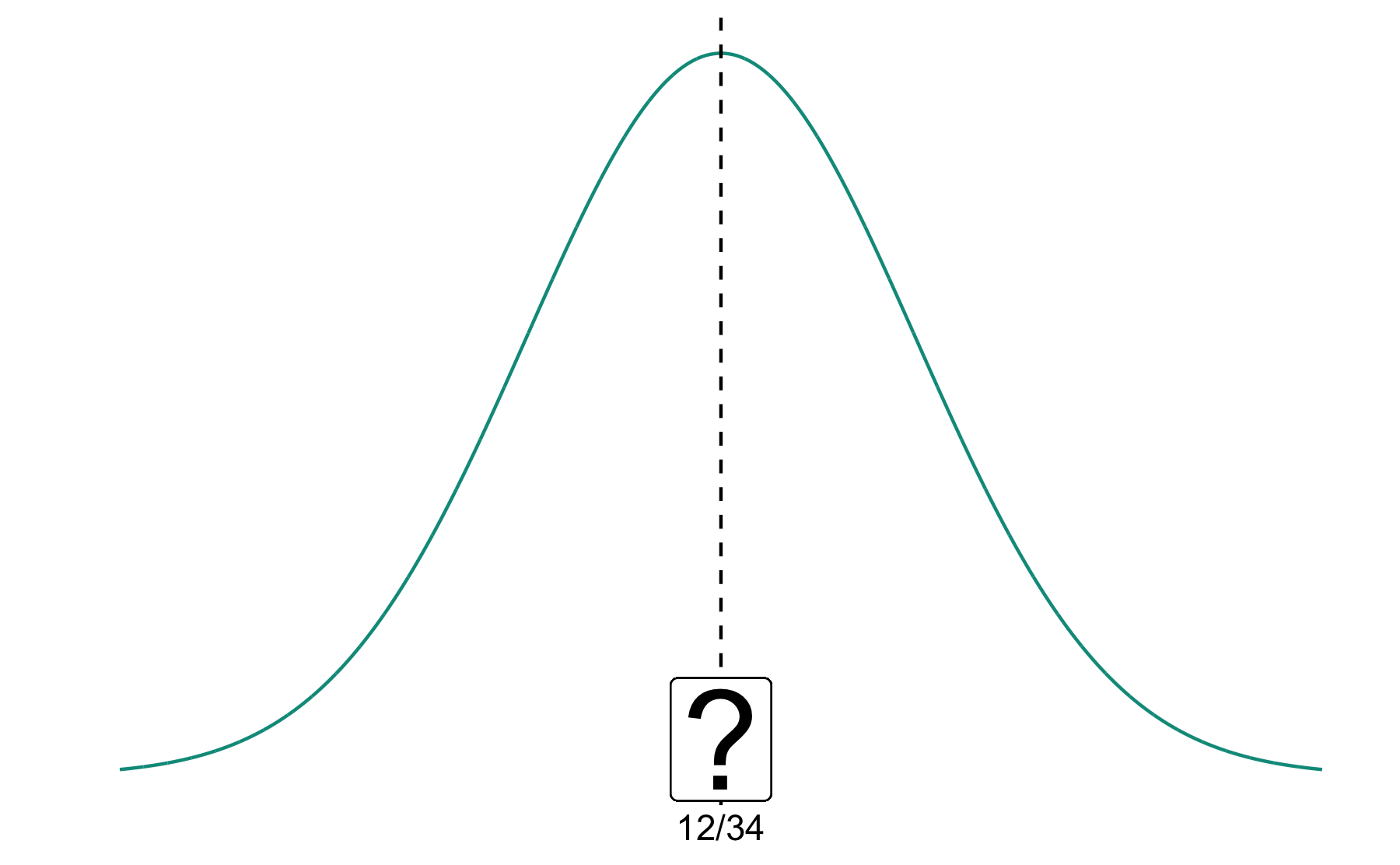
Was ist der wahre Erschmecker-Anteil?
Anteil Stichprobe: 12/34
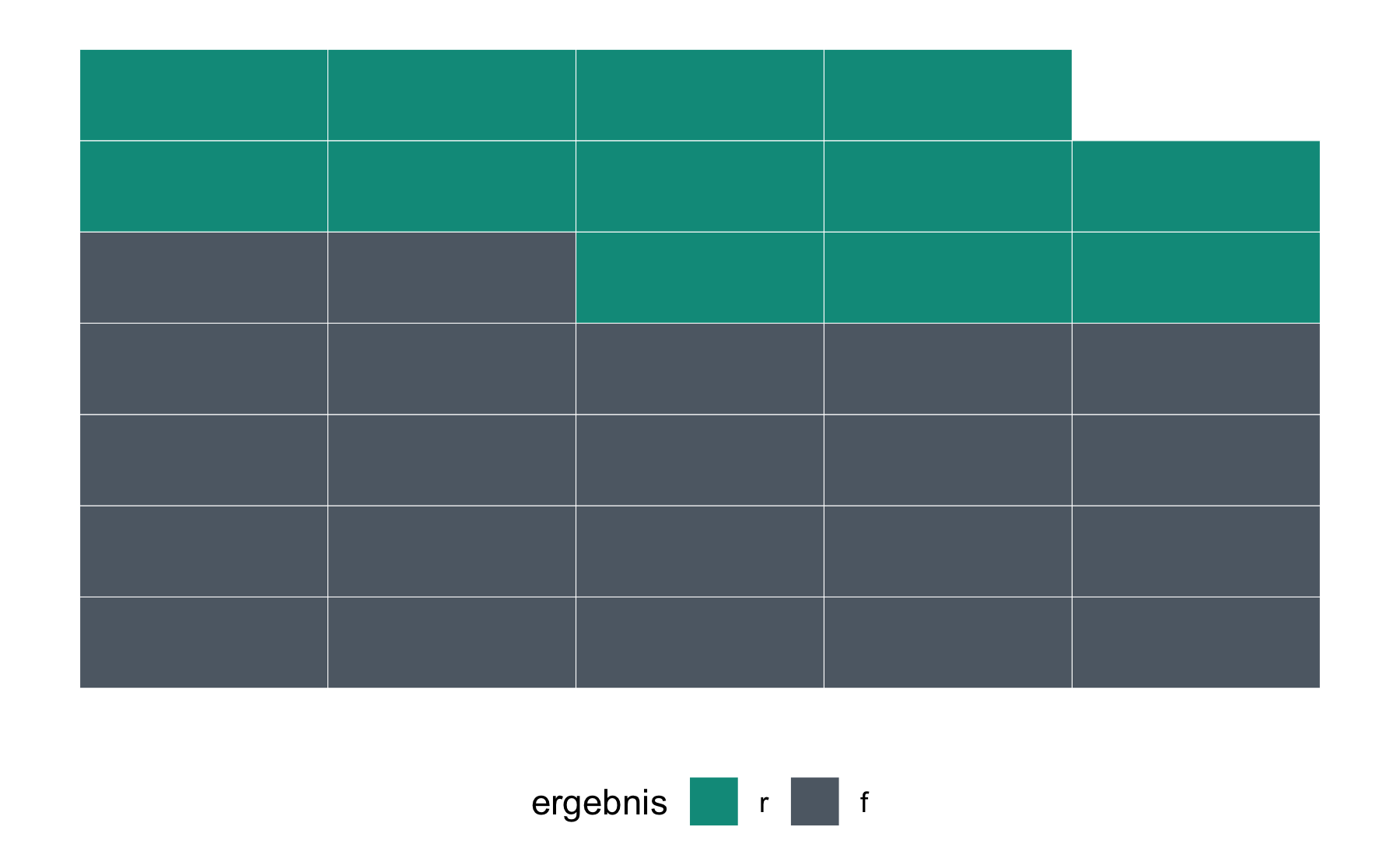
Anteil in Population der FOM-Profs???
Idee 1: Wir testen alle FOM-Profs!

super. Dauert aber.
Idee 2: Wir wiederholen der Versuch oft!
z.B. 100 Mal:
super. Dauert aber.
Idee 3: Der Münchhausen-Trick
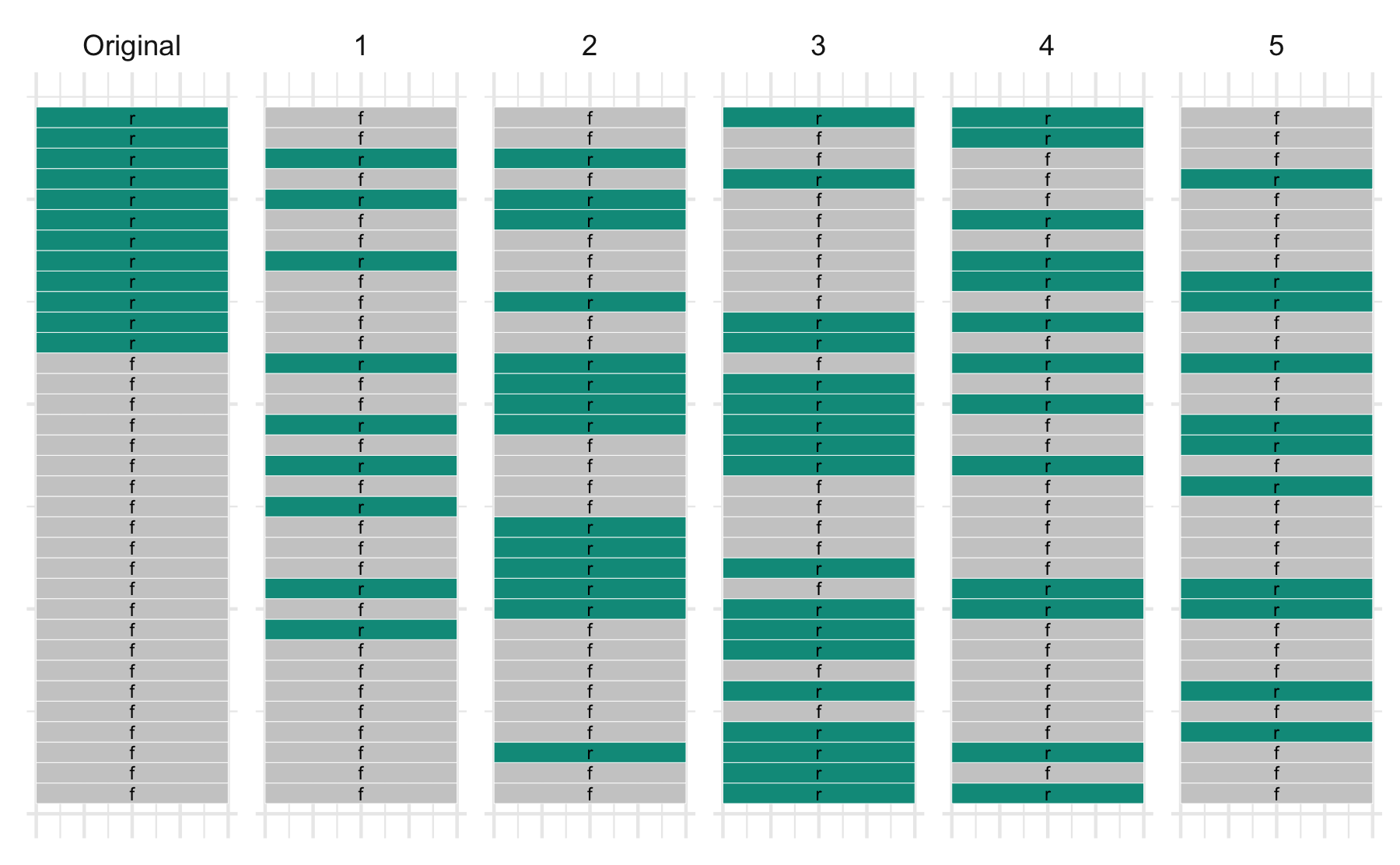
Ziele viele Stichproben mit Zurücklegen
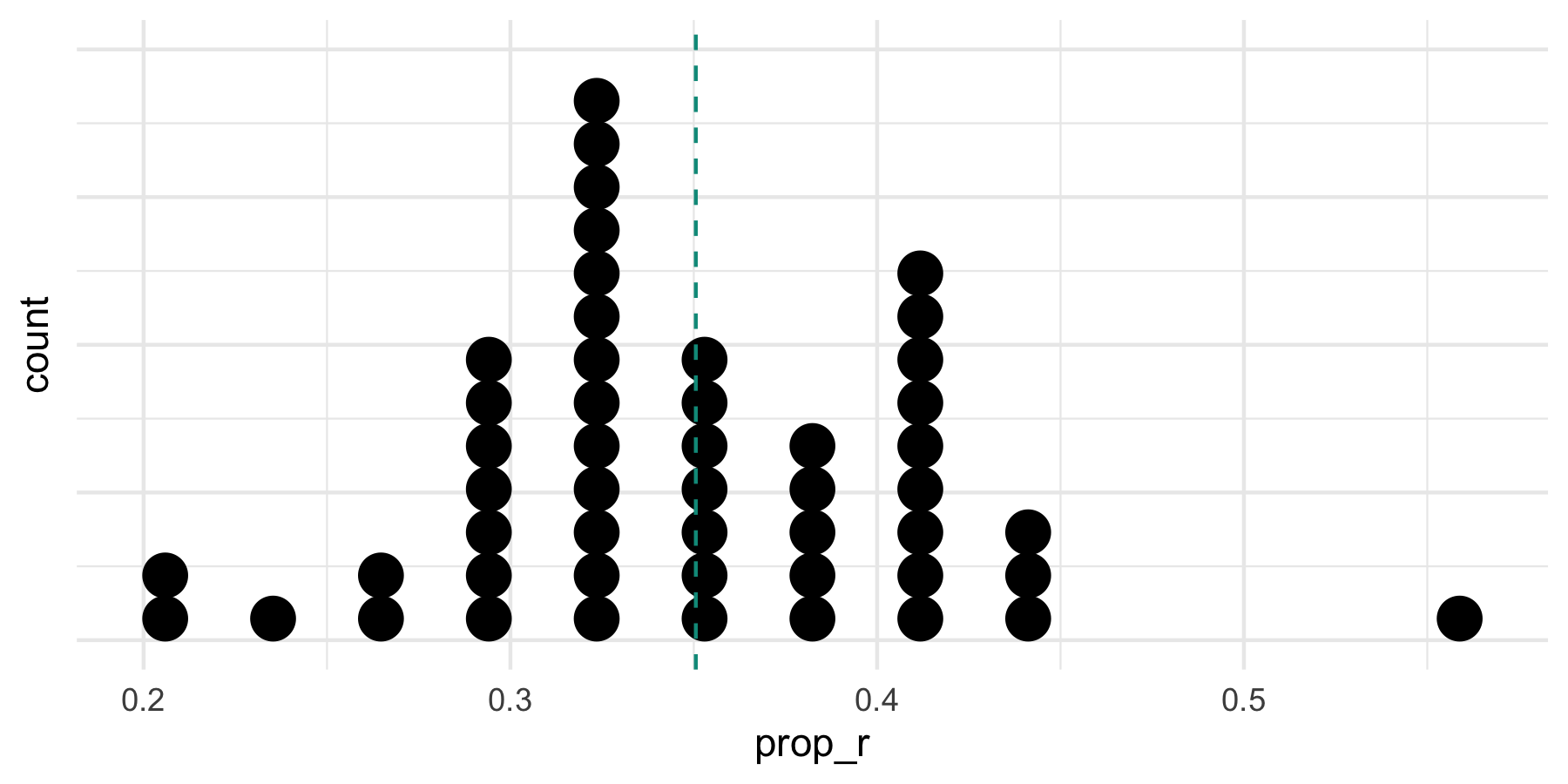
Voila -- Die Bootstrap-Verteilung:
Auf Errisch geht das so...
library(mosaic)# unsere Stichprobe:stipro <- rep(factor(c("f","r")), c(22, 12)) # 3 Bootstrap-Stichproben:boot1 <- mosaic::do(3) * prop( ~ resample(stipro), success = "r") boot1#> prop_r#> 1 0.3529412#> 2 0.3823529#> 3 0.3529412# Histogramm zeichnen:gf_bar( ~ prop_r, data = Bootvtlg)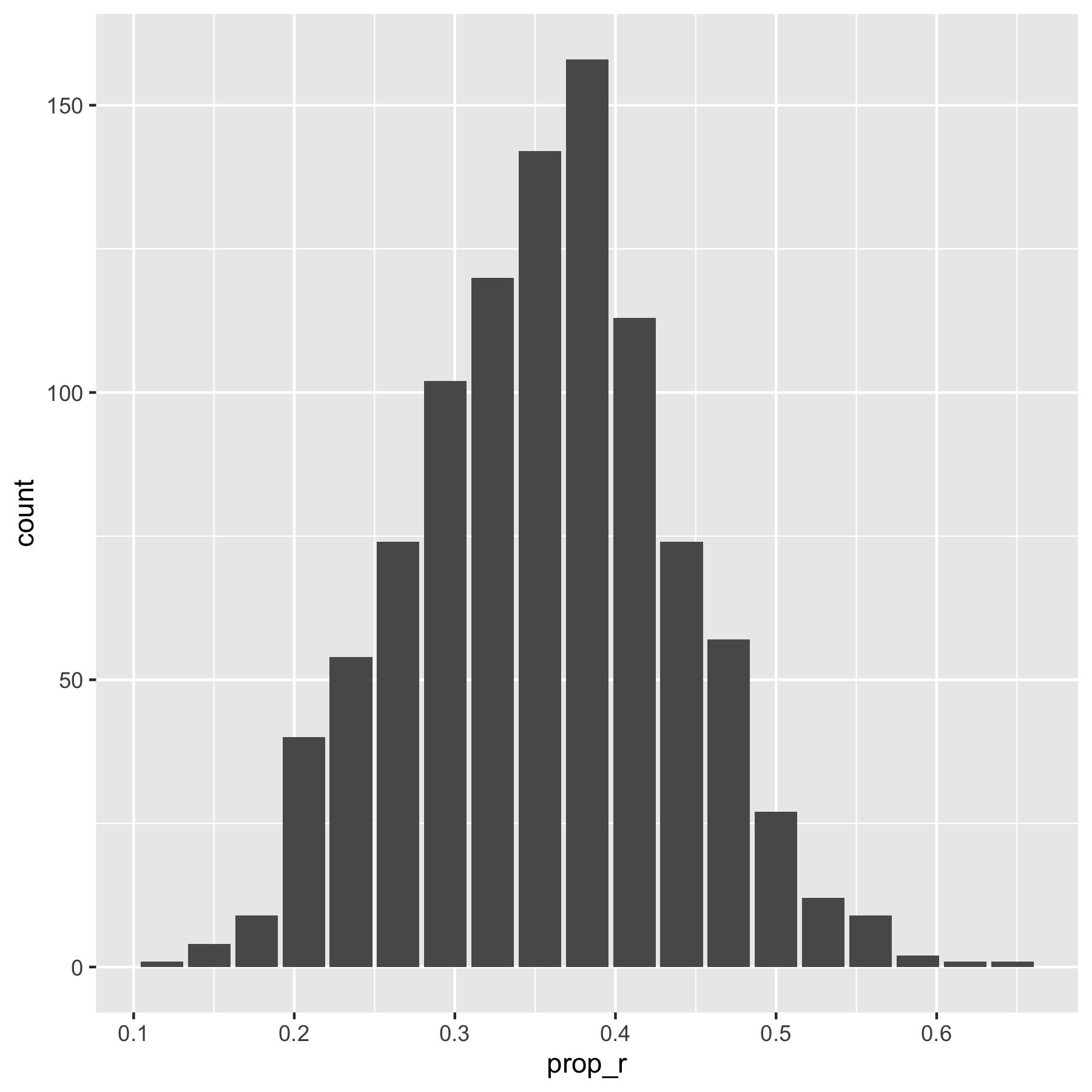
Bootstrap-Kochrezept
Voraussetzungen
- Zufallsstichprobe
- Nicht zu kleine Stichprobe, \(n\ge35\)
Ablauf
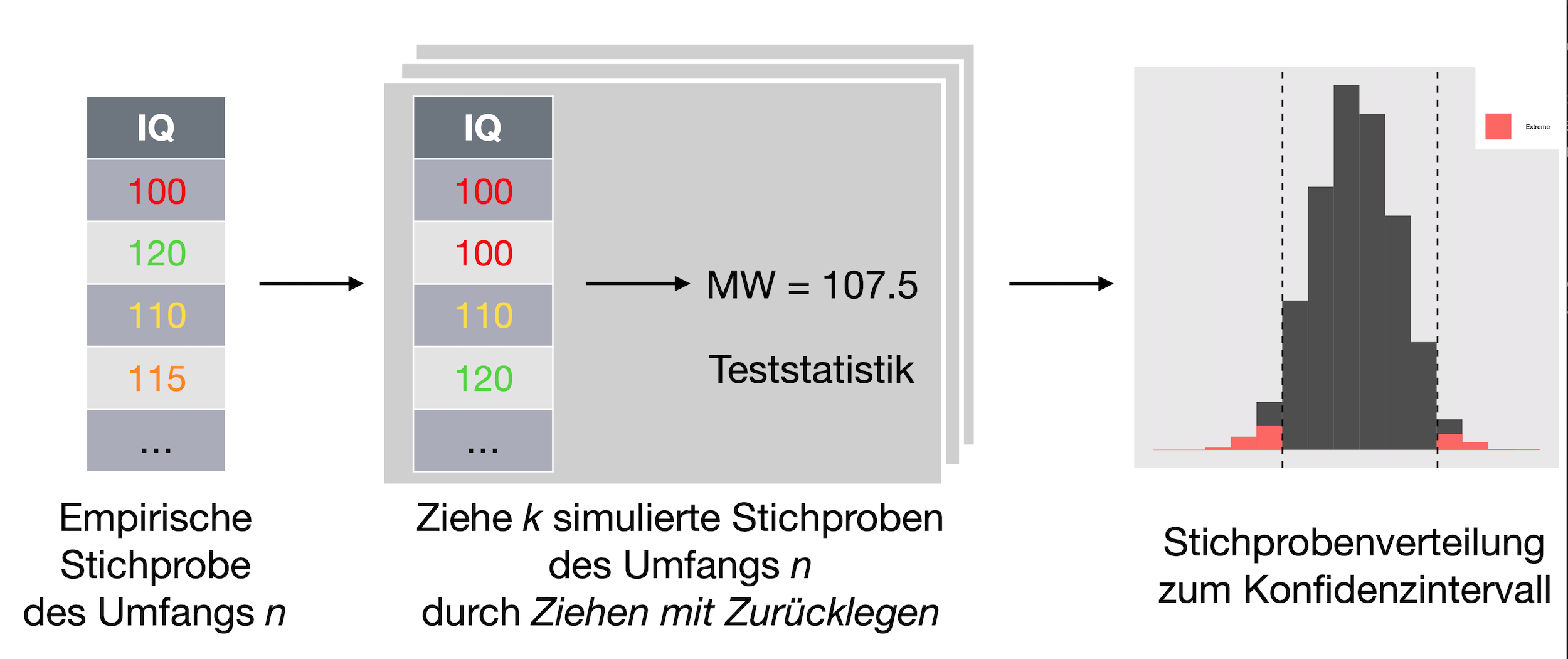
Ziehe 1000 Bootstrap-Stichproben
Berechne jeweils Statistik (z.B. Anteil)
Sortiere die Stichproben nach ihrem Wert
Zeichne Histogram
Schneide links/rechts jeweils 25 Stichproben ab
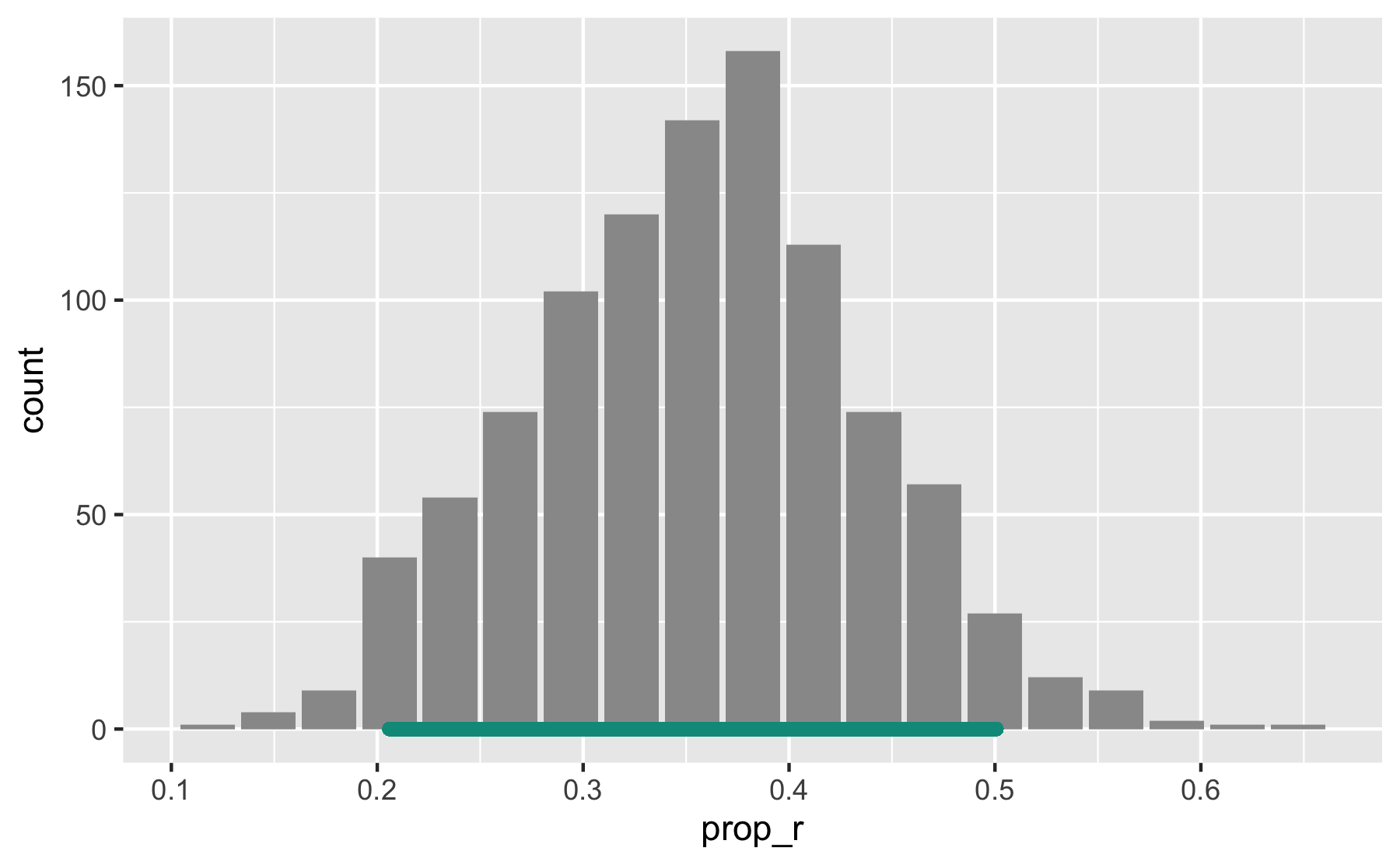
Übung: Ist 1/3 ein plausibler Wert in der FOM-Prof-Population?
🏋️♀️
boot2 <- mosaic::do(1000) * prop( ~ resample(stipro), success = "r")confint(boot2)#> name lower upper level method estimate#> 1 prop_r 0.2058824 0.5294118 0.95 percentile 0.3529412
3 Der Pringels-Test -- Hypothesen testen, Teil 1
Echte Pringels kann man nicht rausschmecken (?)
Übung: Rate-Wahrscheinlichkeit
🏋️♀️
Wie groß ist die Wahrscheinlichkeit \(\pi\), einen Pringel unter drei Proben rein zufällig, also durch Raten, herauszuschmecken?
A. \(\pi = 0\)
B. \(\pi = 1/3\)
C. \(\pi = 1/2\)
D. \(\pi = 2/3\)
B. \(\pi = 1\)
"Pringels kann man nicht rausschmecken!"
\(H_0: \pi \le 1/3\).
\(H_A: \pi > 1/3\).
Angenommen, Pringels schmecken genau wie NoName-Chips
dann: Trefferchance = 1/3
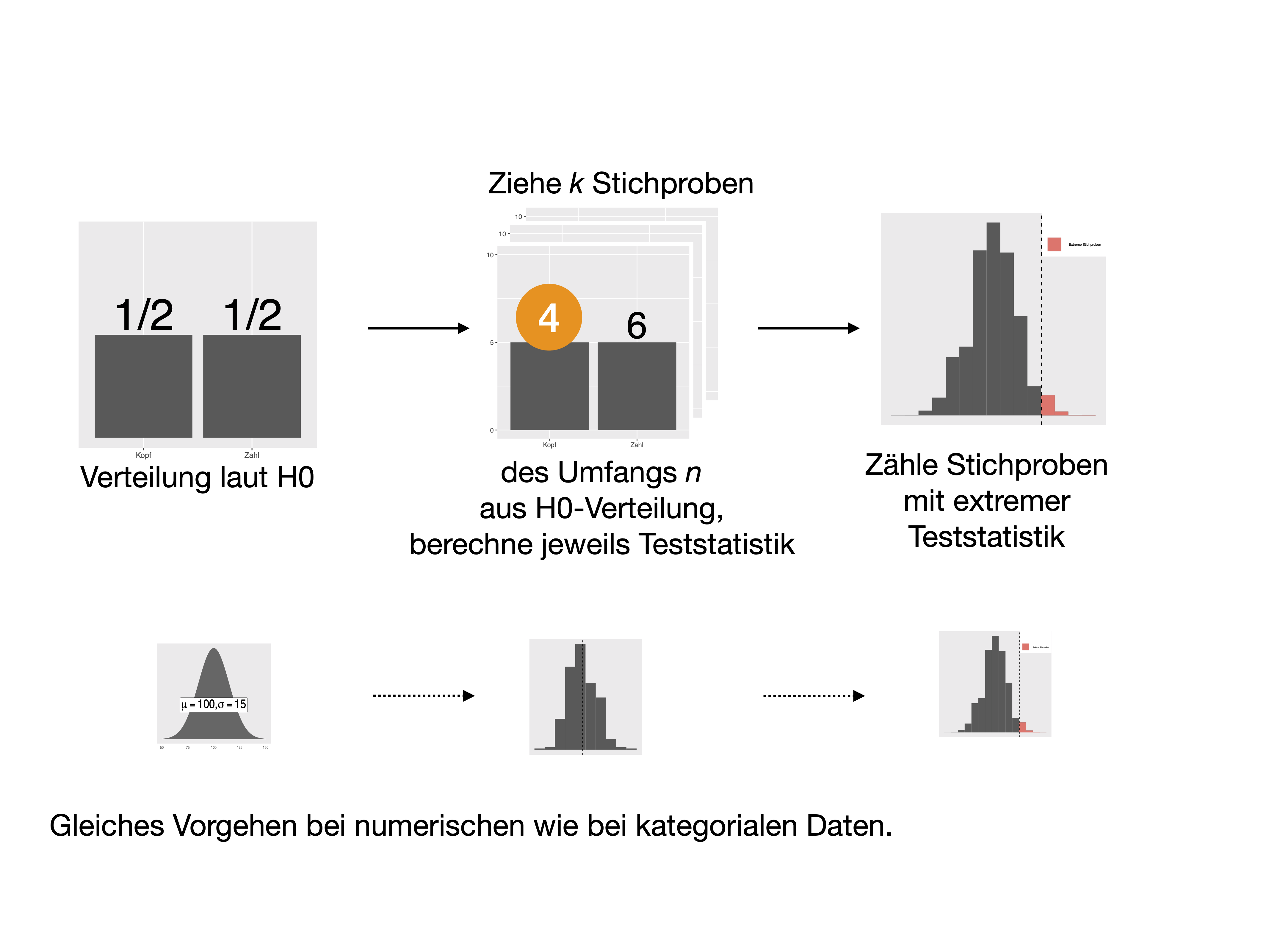
Stellen wir den Versuch anhand von Münzwürfen nach
Werfen wir eine gezinkte Münze (Trefferquote 1/3):
rflip(prob = 1/3)#> #> Flipping 1 coin [ Prob(Heads) = 0.333333333333333 ] ...#> #> T#> #> Number of Heads: 0 [Proportion Heads: 0]Jetzt \(n=34\) gezinkte Münzen:
rflip(n = 34, prob = 1/3)#> #> Flipping 34 coins [ Prob(Heads) = 0.333333333333333 ] ...#> #> T T T T T T T T H T H T T H H T T H H T H H T T H T H T T T T T T T#> #> Number of Heads: 10 [Proportion Heads: 0.294117647058824]Wir simulieren den Versuch oft ein paar Mal
rflip(n = 34, prob = 1/3)#> #> Flipping 34 coins [ Prob(Heads) = 0.333333333333333 ] ...#> #> T H T H T T H T T T T H T T T T T T H H H T H H T T H T H H T T H T#> #> Number of Heads: 13 [Proportion Heads: 0.382352941176471]rflip(n = 34, prob = 1/3)#> #> Flipping 34 coins [ Prob(Heads) = 0.333333333333333 ] ...#> #> T H H T T T T T T H H T H H T H H T T T T T T H T T T T H T H T H H#> #> Number of Heads: 13 [Proportion Heads: 0.382352941176471]...
Wir erzeugen 1000 Rate-Stichproben
Nullvtlg <- mosaic::do(10000) * rflip(n = 34, prob = 1/3)gf_bar( ~ heads, data = Nullvtlg )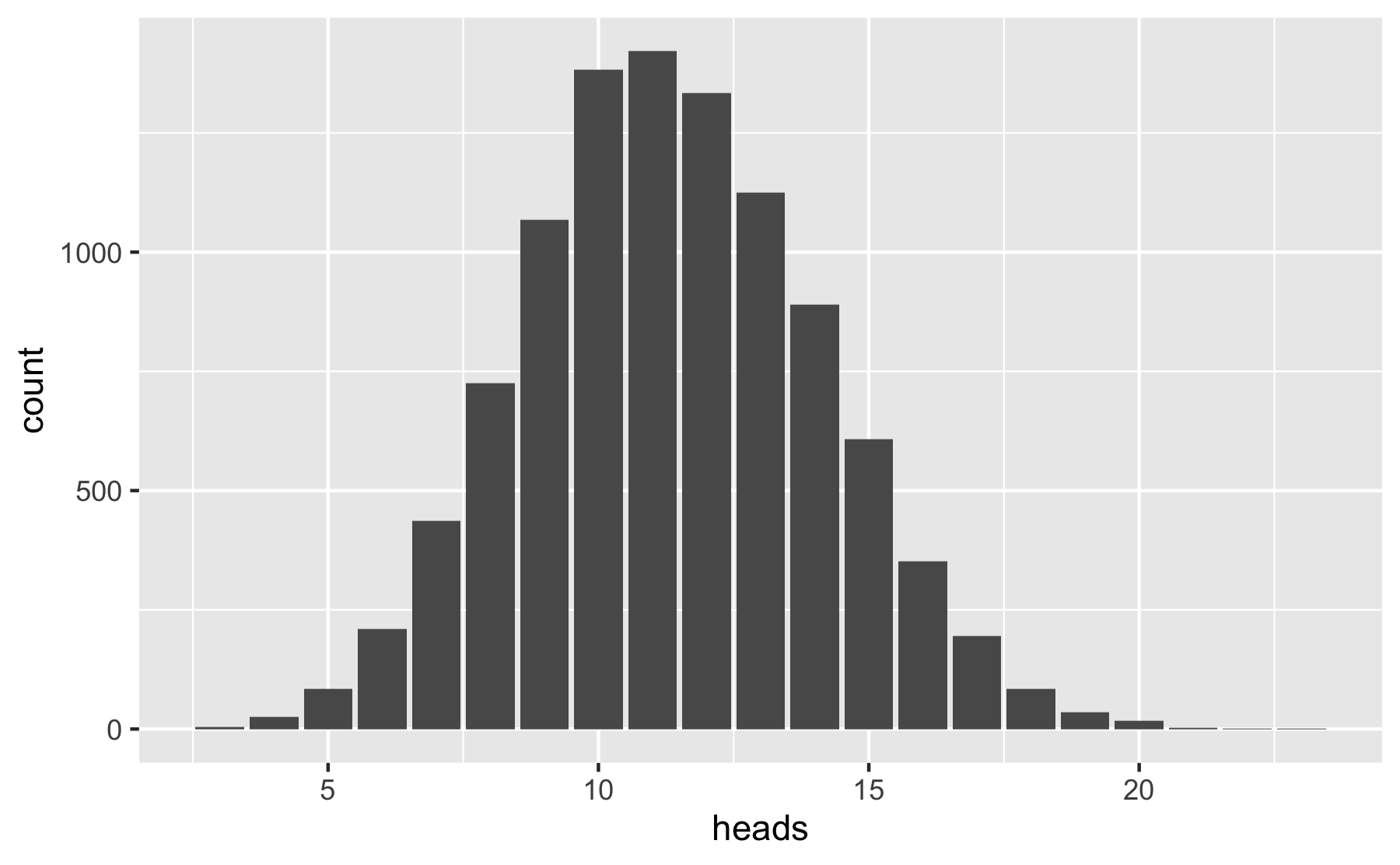
Die Blaupause eines (jeden) statistisches Tests
p-Wert
p-Wert: Anteil der Stichproben mit mindestens 12 Treffer:
gf_bar( ~ heads, data = Nullvtlg)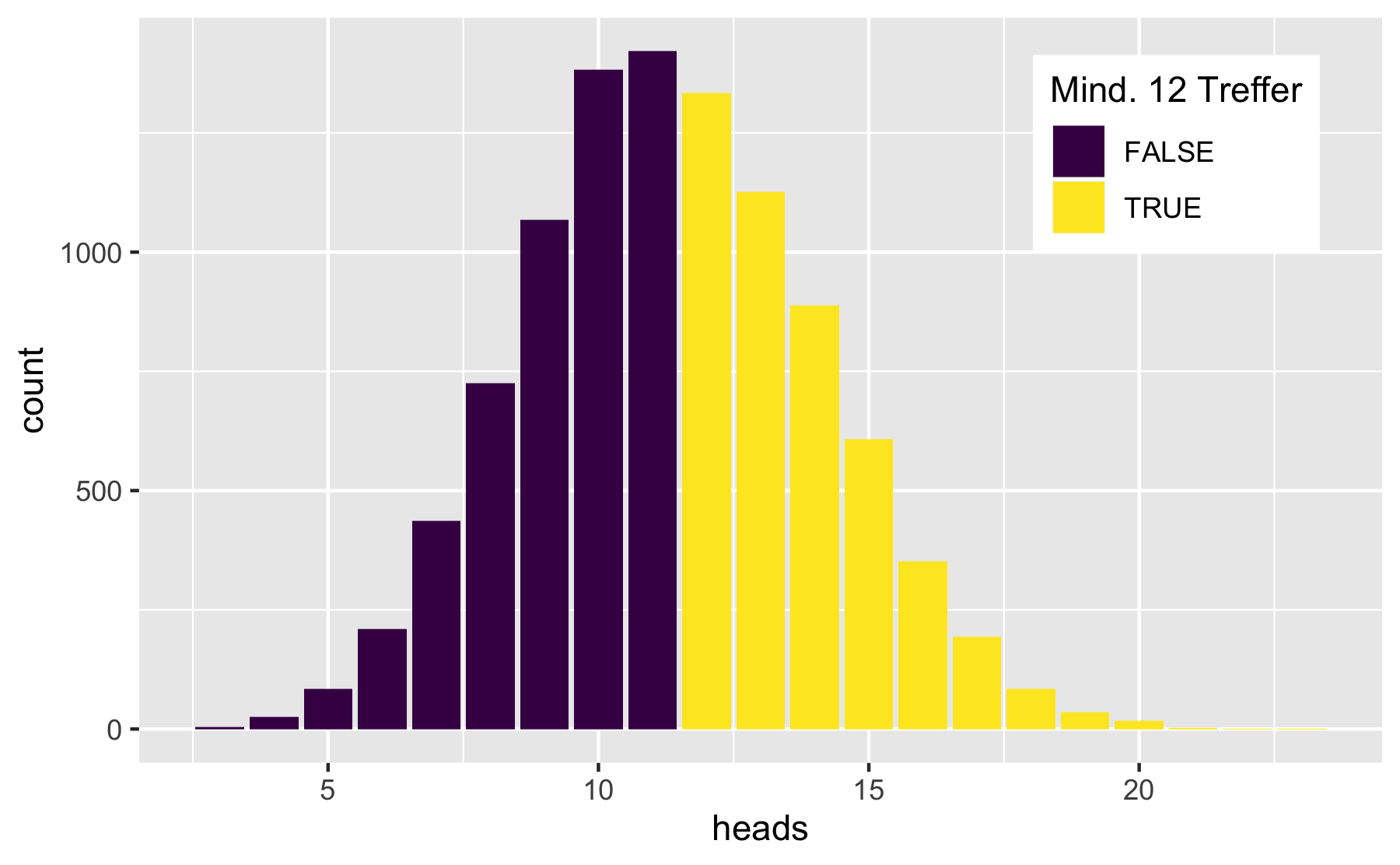
prop( ~ heads >= 12, data = Nullvtlg)#> prop_TRUE #> 0.4644Als sehr, sehr wichtig

... wird der p-Wert von vielen erachtet.
Die Daten sind plausibel unter der Nullhypothese.
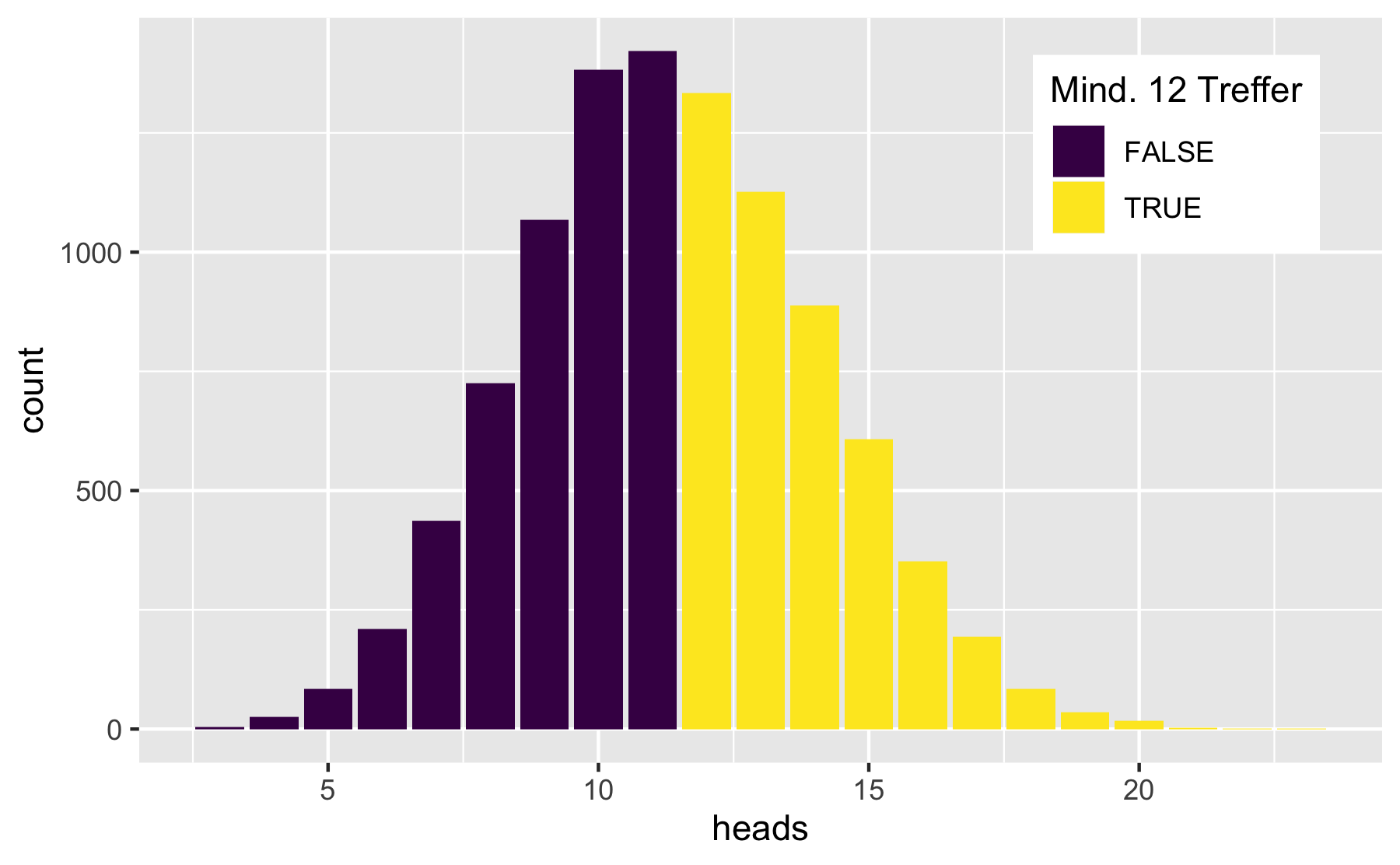
Die Daten sind mit der \(H_0\) kompatibel.
Wir können die Nullhypothese also nicht ablehnen.
p-Wert: Eine gute Geschichte
... verdient, aufgebauscht zu werden (?)

www.xkcd.com/about Note: You are welcome to reprint occasional comics pretty much anywhere (presentations, papers, blogs with ads, etc). If you're not outright merchandizing, you're probably fine. Just be sure to attribute the comic to xkcd.com.
Forschung über dem 5%-Niveau
"... some statisticians prefer to supplement or even replace p-values with other approaches. These include methods that emphasize estimation over testing, such as confidence ... intervals ..."
"Good statistical practice ... emphasizes principles of good study design ... , a variety of numerical and graphical summaries of data, understanding of the phenomenon under study, interpretation of results in context, complete reporting and proper logical and quantitative understanding of what data summaries mean."
... No single index should substitute for scientific reasoning.
Ronald L. Wasserstein & Nicole A. Lazar (2016) The ASA Statement on p-Values: Context, Process, and Purpose, The American Statistician, 70:2, 129-133, DOI: 10.1080/00031305.2016.1154108
Gott liebt
... 0.051 fast genauso sehr wie 0.049
Im Übrigen ...
I have no interest in you or your life.
— God (@TheTweetOfGod) January 4, 2019
Gelman, A., & Stern, H. (2006). The Difference Between “Significant” and “Not Significant” is not Itself Statistically Significant. The American Statistician, 60(4), 328–331. https://doi.org/10.1198/000313006X152649
4 Die Lächelstudie -- Hypothesen testen, Teil 2
Stimmt Lächeln nachsichtiger?
Stimmt Lächeln nachsichtiger?
Skeptiker:
"Lächeln bringt doch nichts!"
\(H_0: \mu_{\text{Lächeln}} \le \mu_{\text{Neutral}}\)
\(H_A: \mu_{\text{Lächeln}} > \mu_{\text{Neutral}}\)
LaFrance, M., & Hecht, M. A. (1995). Why smiles generate leniency. Personality and Social Psychology Bulletin, 21(3), 207-214, https://doi.org/10.1177%2F0146167295213002
Finde den echten Datensatz
11 Datensätze wurden so simuliert, dass es keinen Unterschied in den Mittelwerten der Populationen gibt, 1 Datensatz ist echt.
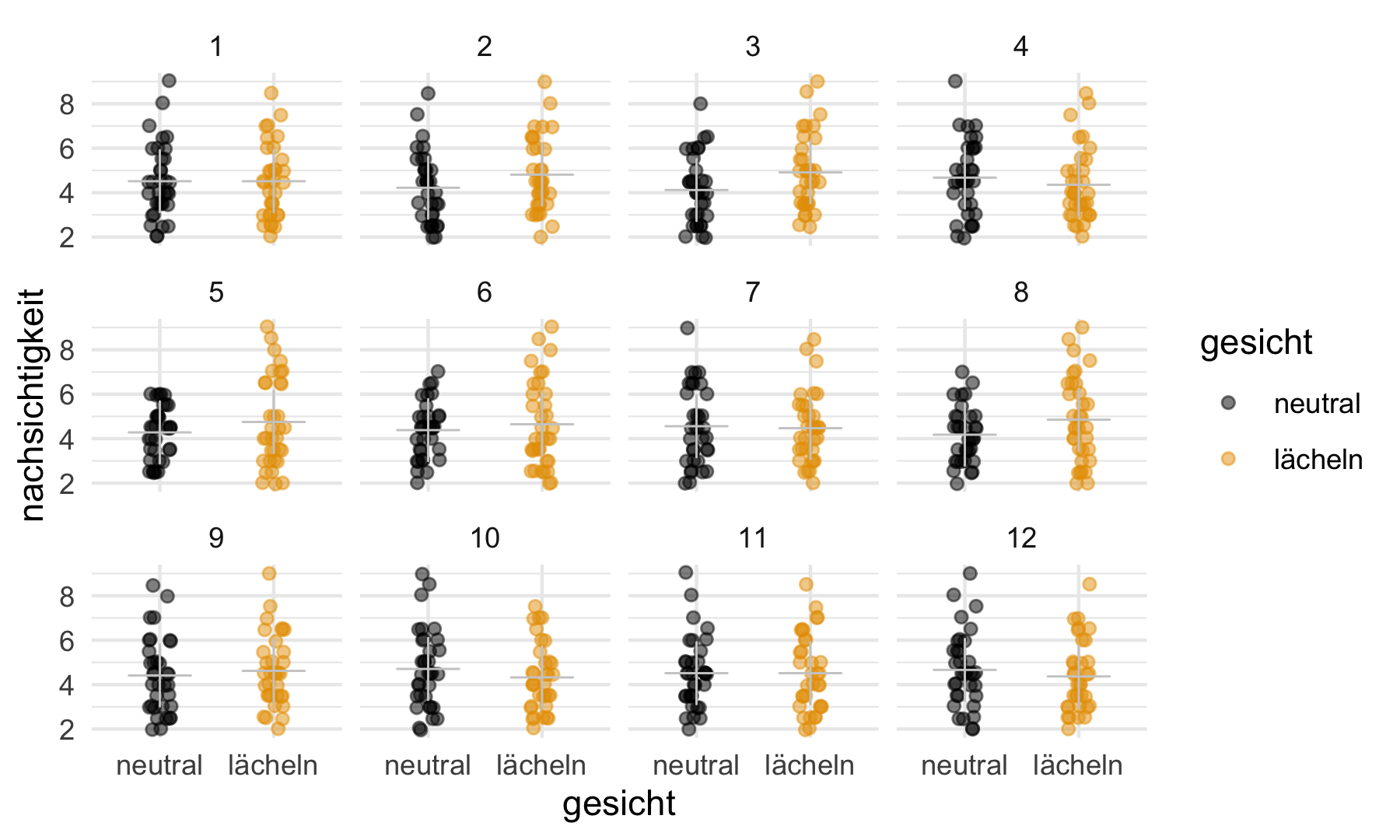
Angenommen, es gäbe keinen Zusammenhang
... von Lächeln und Nachsichtigkeit. Wie häufig wäre unser empirischer Wert in diesen Stichproben?
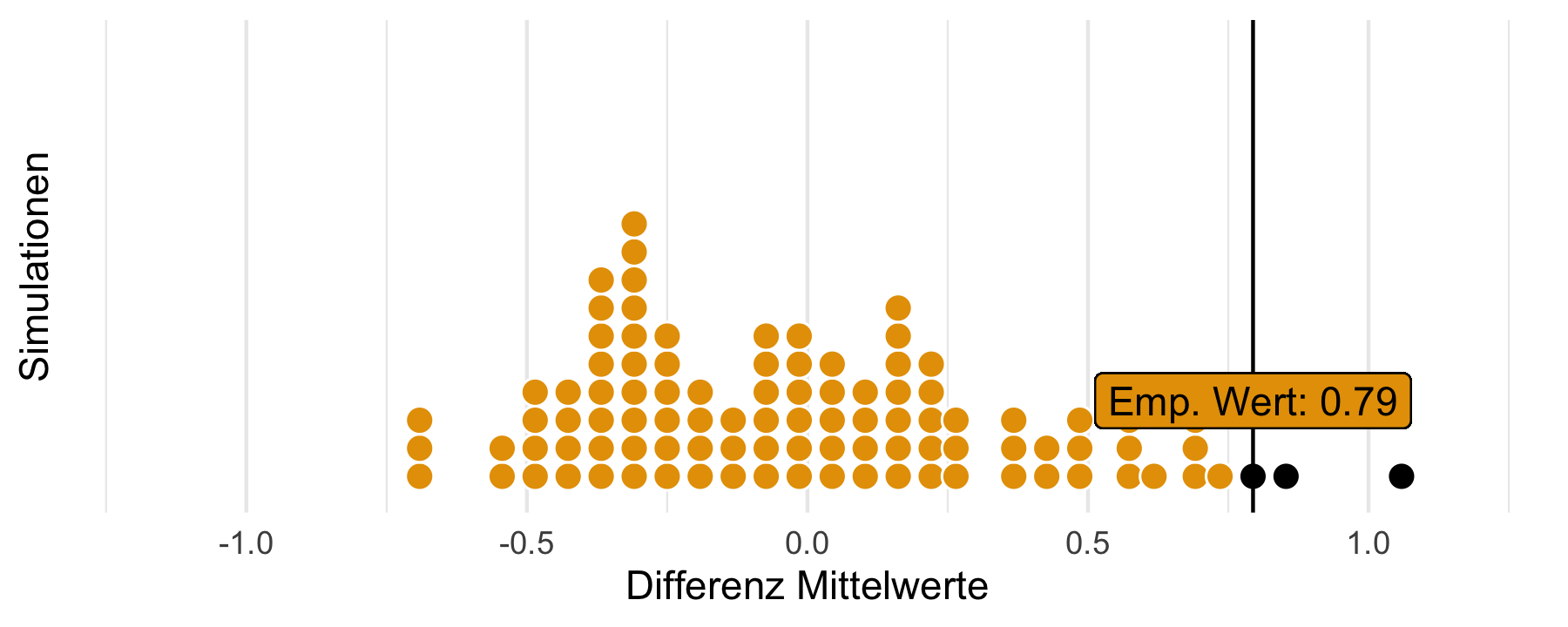
Der p-Wert schlägt zurück
Wenn die Daten aus einer Population stammen, in der die Nullhypothese stimmt, dann ist unser empirisches Ergebnis selten (unplausibel).
Auf dieser Basis entscheiden wir uns in diesem Fall, die \(H_0\) zu verwerfen (bzw. nicht mehr so stark wie vorher an sie zu glauben).
Wie stellt man die Nullverteilung her?
1.
Man reist in ein Land, in dem es keinen Zusammenhang gibt (zwischen Lächeln und Nachsichtigkeit) und zieht dort viele Stichproben.
... Oder man mischt eine Spalte
2.
Man mischt die Spalte (z.B. UV) durch, so dass der Zusammenhang zwischen der Spalte UV under einer anderen Spalte (AV) aufgelöst wird.
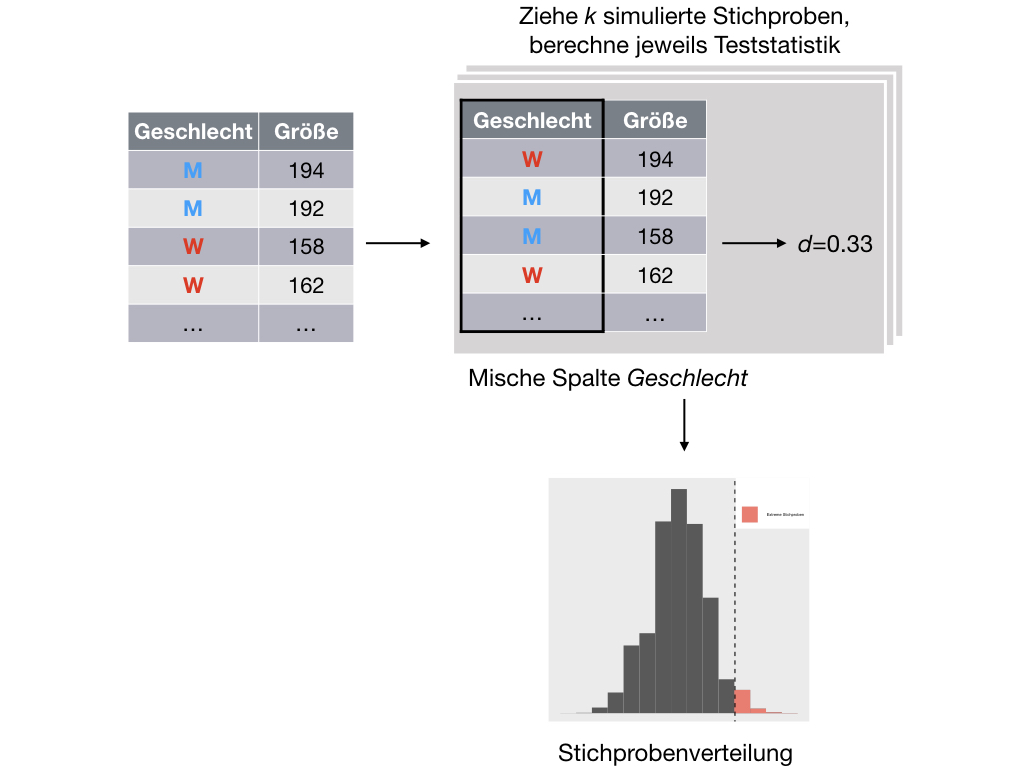
So mischt man eine Spalte mit R
Nullvtlg_gesicht <- mosaic::do(100)*diffmean(nachsichtigkeit ~ shuffle(gesicht), data = Laecheln)gesicht gesicht_gemischt nachsichtigkeit
lächeln neutral 7.0 lächeln neutral 3.0 lächeln lächeln 6.0 lächeln lächeln 4.5 lächeln neutral 3.5 lächeln lächeln 4.0
Übung: Konsumieren Raucher im Schnitt mehr? (1/3)
\(H0: \mu_R = \mu_{NR}\)
\(H_A: \mu_r \ne \mu_{NR}\)
Daten laden:
download.file("https://goo.gl/whKjnl", destfile = "tips.csv")tips <- read.csv2("tips.csv")Nullverteilung berechnen:
library(mosaic)Nullvtlg_Raucher <- mosaic::do(1000) * diffmean(total_bill ~ shuffle(smoker), data = tips)Die ersten paar Werte aus den Stichproben der Nullverteilung:
| diffmean |
|---|
| -1.2006729 |
| 1.5180254 |
| 2.1377989 |
| 0.2732657 |
| 1.6922987 |
| 0.0890885 |
Übung: Konsumieren Raucher im Schnitt mehr? (2/3)
\(H_0\)-Verteilung visualisieren:
gf_histogram( ~ diffmean, data = Nullvtlg_Raucher) %>%gf_vline(xintercept = ~diffmean(total_bill ~ smoker, data = tips))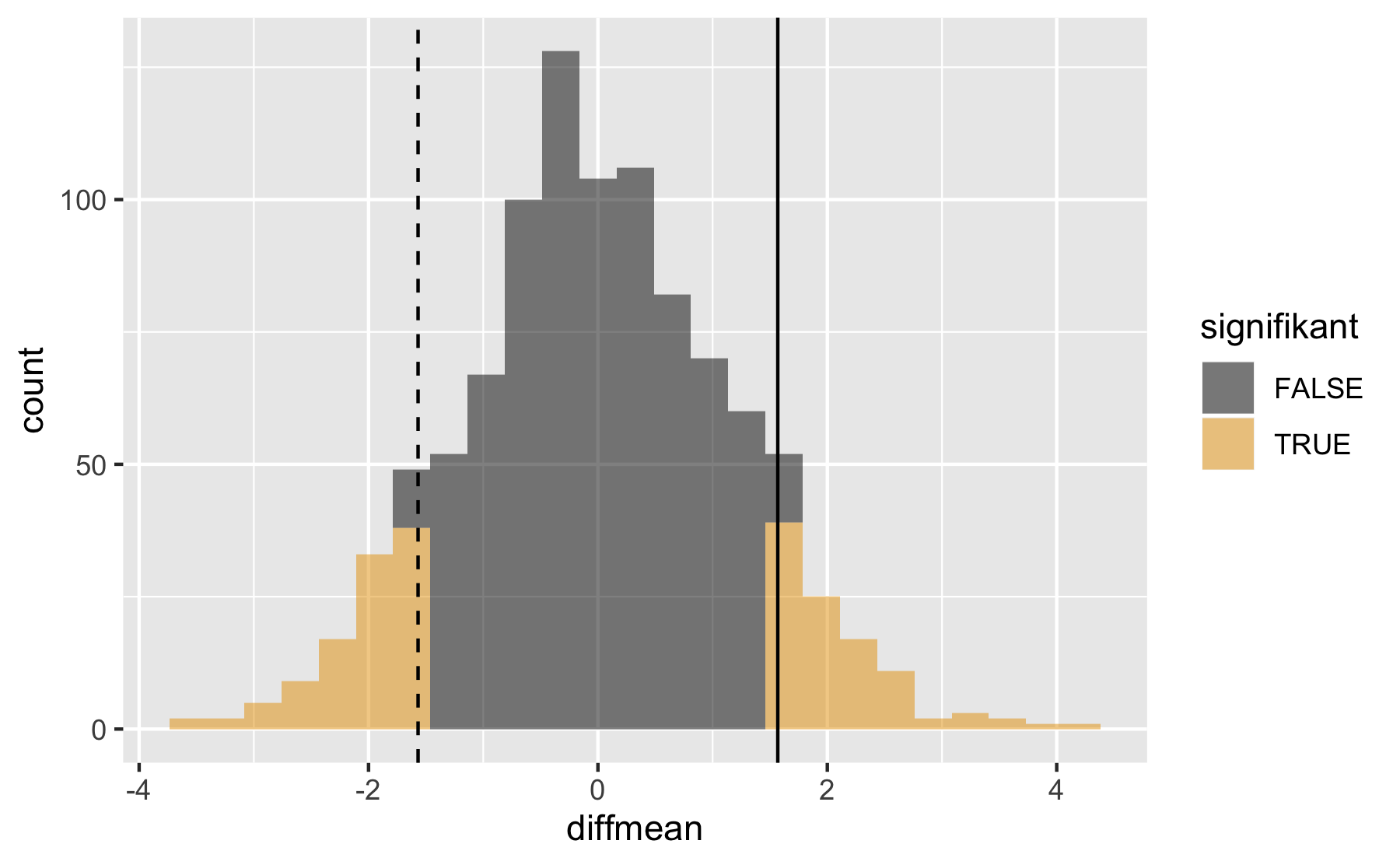
Übung: Konsumieren Raucher im Schnitt mehr? (2/3)
Empirische Differenz/Wert in der Stichprobe:
#> diffmean #> 1.568066Anteil der Stichproben, die mind. so groß sind wie der emp. Wert:
#> prop_TRUE #> 0.099Mal zwei nehmen, da ungerichtete Hypothese:
#> prop_TRUE #> 0.198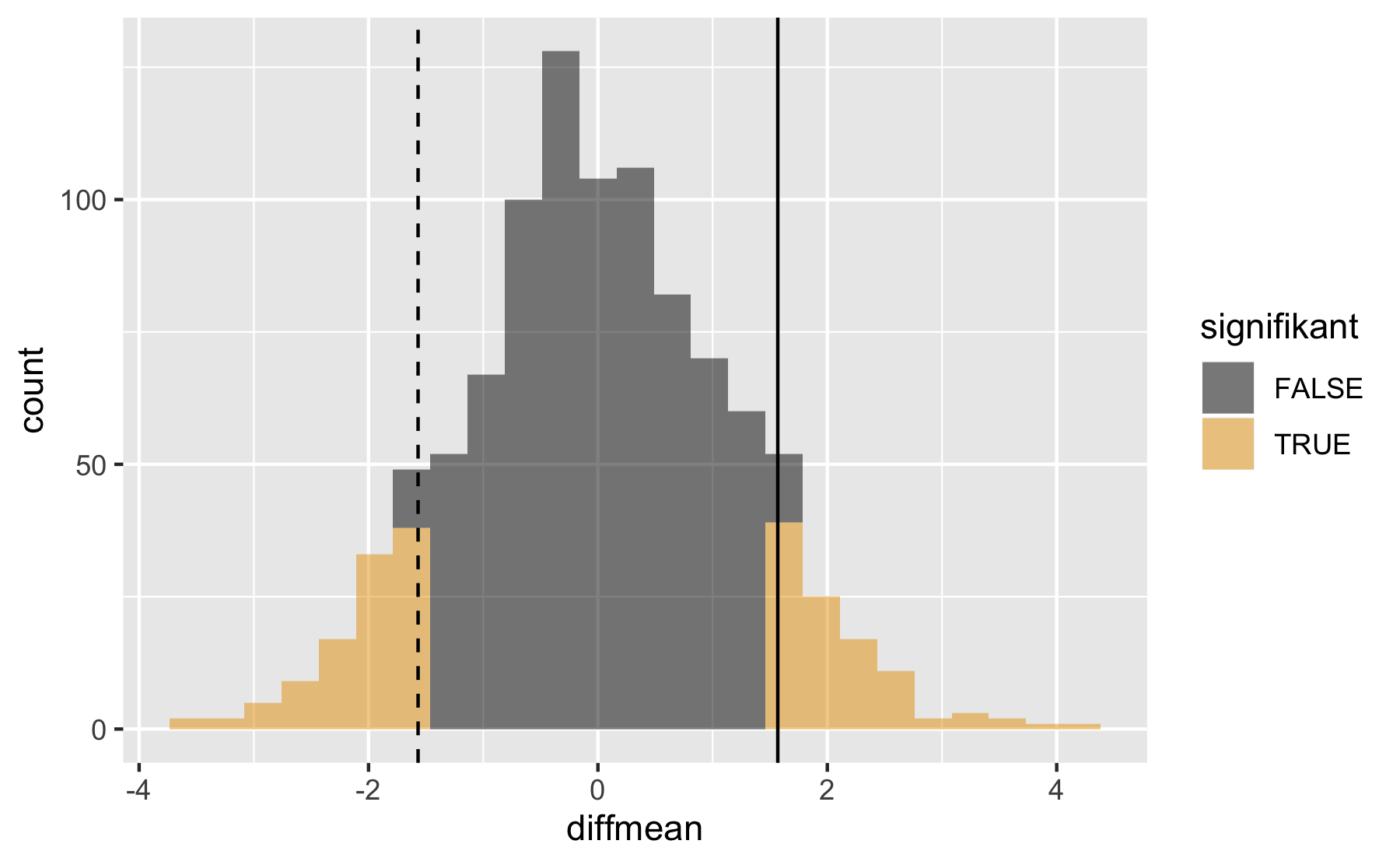
5 Fazit
Wie war das nochmal im Mittelteil?
Verteilungsbasiert vs. simulationsbasiert

Drei Varianten von Simulationstechniken
1. Bootstrapping: Ziehe viele Stichproben mit Zurücklegen aus Originalstichprobe, um Konfidenzintervall zu erhalten
2. Permutationtest: Testen von Zusammenhangs-/Unterschiedshypothesen
3. Einfache Simulation: Führe den Versuch oft durch, unter Annahme von \(H_0\)
Drei Varianten von Simulationstechniken -- mit R
1. Bootstrapping: Ziehe viele Stichproben mit Zurücklegen aus Originalstichprobe, um Konfidenzintervall zu erhalten
do(oft) * statistik(y ~ x, data = resample(Daten))2. Permutationtest: Testen von Zusammenhangs-/Unterschiedshypothesen
do(oft) * statistik(y ~ shuffle(x), data = Daten)3. Einfache Simulation: Führe den Versuch oft durch, unter Annahme von \(H_0\)
do(oft) * ziehe_aus_verteilung(n, parameterwerte)Übersicht Teststatistiken (Auswahl)
| Y | X | Statistik |
|---|---|---|
| binär | NA | Anteil `\(p\)` |
| kategorial | NA | Verhältnis beobachtet/erwartet: `\(\chi^2\)` |
| kategorial | NA | Verhältnis beobachtet/erwartet": `\(\chi^2\)` |
| numerisch | NA | Mittelwert `\(\bar{x}\)` |
| binär | binär | Differenz der Anteile `\(p_B-p_A\)` |
| numerisch | binär | Differenz der Mittelwerte `\(\bar{x}_B-\bar{x}_A\)` |
| kategorial | kategorial | Verhältnis beobachtet/erwartet: `\(\chi^2\)` |
| numerisch | kategorial | Verhältnis Varianz zwischen/innerhalb der Gruppen: `\(F\)` |
| numerisch | numerisch | Korrelation oder Regression `\(r \hat{\beta}\)` |
| kategorial | numerisch | Regression `\(\hat{\beta}\)` (logistische oder multinomiale Regression) |
Übersicht Inferenzverfahren R mosaic (Auswahl)
| Y | X | simulationsbasiert | konventionell |
|---|---|---|---|
| binär | . | prop() | binom.test() |
| kategorial | . | xchisq.test() | xchisq.test() |
| kategorial | . | chisq.test() | chisq.test() |
| numerisch | . | mean() | t.test() |
| binär | binär | diffprop() | prop.test() |
| numerisch | binär | diffmean() | t.test() |
| kategorial | kategorial | xchisq.test() | xchisq.test() |
| numerisch | kategorial | aov() | aov() |
| numerisch | numeric | cor(), lm() | cor.test(), lm() |
| kategorial | numerisch | glm(family= 'binomial') | glm(family= 'binomial') |
Nutzen und Grenzen
Ein Prinzip für alle gängigen Verfahren
Wenige Voraussetzungen
Einfach, wenig abstrakt
- Zur Anschlussfähigkeit sollten Namen konventioneller Verfahren (wie t-Test) weiterhin gelehrt werden
Sinnbild: Bootstrap
Sinnbild: Zusammenhang zweier Variablen (Permutationstest)

Sinnbild: Test auf bestimmten Wert einer Variablen
Fragen, Feedback, Feierlichkeiten?
Sprechen Sie uns an!
sebastian.sauer@fom.de
Diese Folien wurden von Autor*innen der FOM https://www.fom.de/ entwickelt und stehen unter der Lizenz CC-BY-SA-NC 3.0 de: https://creativecommons.org/licenses/by-nc-sa/3.0/de/
Technical details
Last update: 2020-02-03
Slides built with
xaringan, based onrmarkdownPackages: assertthat 0.2.1, backports 1.1.5, broom 0.5.3, cellranger 1.1.0, cli 2.0.1, codetools 0.2-16, colorspace 1.4-1, cowplot 1.0.0, crayon 1.3.4, crosstalk 1.0.0, curl 4.3, DBI 1.1.0, dbplyr 1.4.2, digest 0.6.23, dplyr 0.8.3, DT 0.11, emo 0.0.0.9000, evaluate 0.14, extrafont 0.17, extrafontdb 1.0, fansi 0.4.1, fastmap 1.0.1, forcats 0.4.0, fs 1.3.1, generics 0.0.2, ggdendro 0.1-20, ggformula 0.9.2, ggplot2 3.2.1, ggrepel 0.8.1, ggstance 0.3.3, glue 1.3.1.9000, gridExtra 2.3, gtable 0.3.0, haven 2.2.0, highr 0.8, hms 0.5.3, htmltools 0.4.0, htmlwidgets 1.5.1, httpuv 1.5.2, httr 1.4.1, icon 0.1.0, jsonlite 1.6, kableExtra 1.1.0, knitr 1.27, later 1.0.0, lattice 0.20-38, lazyeval 0.2.2, leaflet 2.0.3, lifecycle 0.1.0, lubridate 1.7.4, magrittr 1.5, MASS 7.3-51.5, Matrix 1.2-17, mime 0.8, modelr 0.1.5, mosaic 1.5.0, mosaicCore 0.6.0, mosaicData 0.17.0, munsell 0.5.0, nlme 3.1-143, pillar 1.4.3, pkgconfig 2.0.3, promises 1.1.0, purrr 0.3.3, R6 2.4.1, RColorBrewer 1.1-2, Rcpp 1.0.3, readr 1.3.1, readxl 1.3.1, reprex 0.3.0, rlang 0.4.2, rmarkdown 2.0, rstudioapi 0.10, Rttf2pt1 1.3.8, rvest 0.3.5, scales 1.1.0, sessioninfo 1.1.1, shiny 1.4.0, stringi 1.4.5, stringr 1.4.0, tibble 2.1.3, tidyr 1.0.0, tidyselect 0.2.5, tidyverse 1.3.0, vctrs 0.2.1, viridisLite 0.3.0, waffle 1.0.1, webshot 0.5.2, withr 2.1.2, xaringan 0.13, xfun 0.12, xml2 1.2.2, xtable 1.8-4, yaml 2.2.0, zeallot 0.1.0
For detailed
session_info()check out this text file.Thanks to all the open source developers.

