library(tidyverse)

1 Was ist die Regression?

In diesem Post geht es um die einfache Regression (d.h. mit einem Prädiktor); genauer gesagt um die Frage, wie man auf die Formeln der Koeffizienten der einfachen Regression kommt.

Gehen wir von einigen zweidimensionalen Datenpunkten aus, die zu einem Phänomen gemessen wurden: $(x_{1}, y_{1}), (x_{2}, y_{2}), \dots, (x_{n}, y_{n})$ .

Gehen wir weiter davon aus, dass der Zusammenhang in Wirklichkeit von einer Geraden erklärt werden kann:

$\hat{y} = b_{0} + b_{1} x .$

Eine Gerade kann durch zwei Koeffizienten definiert werden, den Achsenabschnitt $b_{0}$ und die Steigung $b_{1}$ .

Für jeden Datenpunkt $y_{i}$ können wir die Abweichung (den Fehler) zum vorhergesagten Wert $\hat{y_{i}}$ ausrechnen:

$e_{i} = y_{i} - \hat{y_{i}}$

Nennen wir die Summe der quadrierten Fehler $e_{i}$ im Folgenden $Q S$ (für Quadratsumme):

$\begin{aligned} Q S & = \sum_{i = 1}^{n} e_{i}^{2} \\ Q S & = \sum_{i = 1}^{n} (y_{i} - \hat{y_{i}})^{2} \\ Q S & = \sum_{i = 1}^{n} (y_{i} - b_{0} - b_{1} x_{i})^{2} \end{aligned}$

Alle Summen belaufen sich über die Beobachtungen $1, 2, i, . . ., n$ .

Betrachten wir das an einem Datenbeispiel:

d <- mtcars
lm1 <- lm(mpg ~ hp, data = d)

d <-
  d %>% 
  mutate(pred = predict(lm1),
         resid = residuals(lm1))

Jetzt visualisieren wir die Residuen (Abweichungen, Fehler):

ggplot(d, 
       aes(x = hp, y = mpg)) +
  geom_smooth(method = "lm", se = FALSE, color = "dodgerblue") +
  geom_segment(aes(xend = hp, yend = pred), alpha = .5) +
  geom_point() +
  geom_hline(yintercept = mean(d$mpg), 
             color = "grey60", linetype = "dashed") +
  geom_vline(xintercept = mean(d$hp), 
             color = "grey60", linetype = "dashed") + 
  annotate("point", x = mean(d$hp), y = mean(d$mpg),
           size = 5, color = "red", alpha = .5)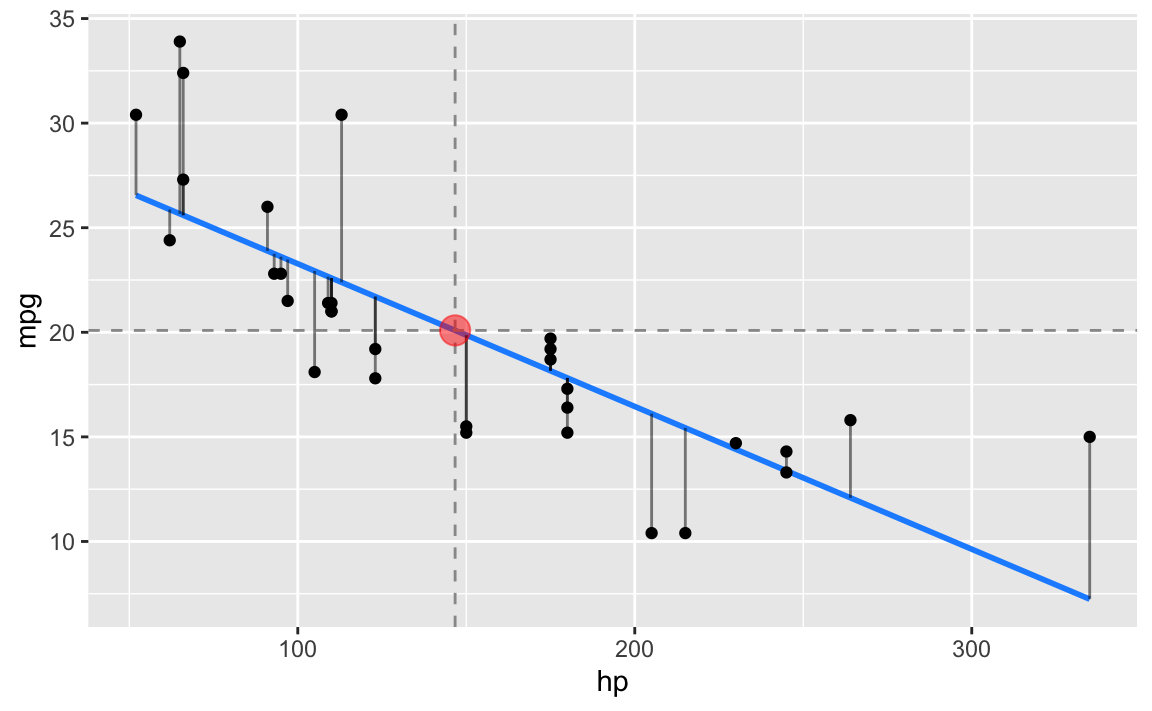

Die blaue Gerade ist die Regressionsgerade; die vertikalen Balken stellen die Residuen dar und die gestrichelten Linien repräsentieren jeweils die Mittelwerte von hp bzw. mpg. Man beachte, dass der Schnittpunkt der Mittelwertslinien auf der Regressionsgeraden liegt.

2 Wie findet man die Regressionsgerade?

Um die Koeffizienten der Regressionsgeraden zu bestimmen, können wir die Methode der kleinsten Quadrate (least squares bzw. ordinary least squares) verwenden. Diese Methode gibt uns diejenigen Koeffizienten der Regressionsgeraden (also $b_{0}$ und $b_{1}$ ), die die Quadratsumme (QS) der Residuen $e_{i}$ minimieren.

Um die Quadratsumme zu minimieren, bilden wir jeweils die erste (parzielle) Ableitung und setzen diese Null. Anschließend löst man nach dem gesuchten Koeffizienten auf. Beginnen wir mit $b_{0}$ .

2.1 $b_{0}$

Wir leiten nach $β_{0}$ ab (Kettenregel) und setzen die Gleichung Null:

$\frac{\partial Q S}{\partial β_{0}} = \sum 2 {(y_{i} - β_{0} - β_{1} x_{i})}^{1} (- 1) = 0$

Teilen durch -2:

$\sum (y_{i} - β_{0} - β_{1} x_{i}) = 0$

Auflösen nach $β_{0}$ , der gesuchten Größe:

$\sum β_{0} = \sum y_{i} - β_{1} \sum x_{i}$ $\sum β_{0} = n β_{0}$ :

$n β_{0} = \sum y_{i} - β_{1} \sum x_{i}$

Teilen durch $n$ :

$\begin{matrix} (1) & β_{0} = \frac{1}{n} \sum y_{i} - β_{1} \frac{1}{n} \sum x_{i} \end{matrix}$

Kürzer fassen:

$β_{0} = \bar{y} - β_{1} \bar{x}$

Das Ergebnis zeigt auch, dass der Punkt $(\bar{x}, \bar{y})$ auf der Regressionsgerade liegt.

2.2 $b_{1}$

Analog verfahren wir für den zweiten Koeffizienten, $b_{1}$ . Wieder bilden wir die parzielle Ableitung, setzen diese Null und lösen nach dem gesuchten Koeffizienten auf. Das Nachdifferenzieren (Kettenregel) liefert allerdings ein anderes Ergebnis:

$\frac{\partial S}{\partial β_{1}} = \sum 2 {(y_{i} - β_{0} - β_{1} x_{i})}^{1} (- x_{i}) = 0$ Gleichung multiplizieren mit $- 1 / 2$ und letzten Faktor, $x_{i}$ nach vorne ziehen:

$\sum x_{i} (y_{i} - β_{0} - β_{1} x_{i}) = 0$ Summenzeichen auflösen:

$\begin{matrix} (2) & \sum x_{i} y_{i} - β_{0} \sum x_{i} - β_{1} \sum x_{i}^{2} = 0 \end{matrix}$

Jetzt setzen wir $(1)$ in $(2)$ ein:

$\sum x_{i} y_{i} - (\frac{1}{n} \sum y_{i} - β_{1} \frac{1}{n} \sum x_{i}) \sum x_{i} - β_{1} \sum x_{i}^{2} = 0$

Klammer auflösen:

$\sum x_{i} y_{i} - \frac{1}{n} \sum x_{i} \sum y_{i} + β_{1} \frac{1}{n} {(\sum x_{i})}^{2} - β_{1} \sum x_{i}^{2} = 0$

Alle Terme mit $β_{1}$ auf die rechte Seite bringen:

$\sum x_{i} y_{i} - \frac{1}{n} \sum x_{i} \sum y_{i} = - β_{1} \frac{1}{n} {(\sum x_{i})}^{2} + β_{1} \sum x_{i}^{2}$

$β_{1}$ vor die Klammer ziehen:

$\sum x_{i} y_{i} - \frac{1}{n} \sum x_{i} \sum y_{i} = β_{1} (\sum x_{i}^{2} - \frac{1}{n} {(\sum x_{i})}^{2})$

Nach $β_{1}$ auflösen:

$β_{1} = \frac{\sum x_{i} y_{i} - \frac{1}{n} \sum x_{i} \sum y_{i}}{\sum x_{i}^{2} - \frac{1}{n} {(\sum x_{i})}^{2}} = \frac{c o v (x, y)}{v a r (x)}$

Wie man sieht, kann $β_{1}$ als das Verhältnis von Kovarianz zu Varianz dargestellt werden.

2.3 Weitere Umformung von $b_{1}$

$\begin{aligned} b_{1} & = \frac{c o v (x, y)}{s^{2} (x)} \\ = \frac{c o v (x, y)}{s^{2} (x)} \cdot \frac{s (y)}{s (y)} \\ = \frac{c o v (x, y)}{s (x) s (y)} \cdot \frac{s (y)}{s (x)} \\ = c o r (x, y) \cdot \frac{s (y)}{s (x)} \end{aligned}$

3 Quellenangabe

Dies Post ist eine kommentierte und leicht angepasste Version von diesem Post auf StackExchange.

4 Fazit

In diesem Post ging es um die Ableitung der Formeln der Regressionskoeffizienten, zumindest der einfachen Regression. Dabei wurden grundlegende Algebra und partielle Ableitungen verwendet. Wir haben also bewiesen, dass die Regressionskoeffizienten die Form haben, wie sie gewöhnlich in einführenden, angewandten Lehrbüchern gezeigt werden.

Für die Ableitung der multiplen Regression sind Ansätze auf Basis der linearen Algebra praktischer.

Ableitung der Koeffizienten der einfachen Regression