Karsten Lübke erstellte die ursprüngliche Version dieser Fallstudie. Sebastian Sauer änderte einige Teile, v.a. zu R, ab.
1 Vorbereitung
1.1 R-Pakete
library(tidyverse)
library(easystats)1.2 Forschungsfrage
- Womit hängt der Energieverbrauch (z.B. Benzin) beim Autofahren zusammen?
Mögliche Einflußfaktoren für \(y\) (Verbrauch) sind u.a.
- Fahrzeugtyp
- Geschwindigkeit
- Fahrtstrecke
- Terrain
- Art des Benzins
- Fahrstil
- Straße
- Temperatur
- Klimanalage
- Gewicht
1.3 Versuchsdaten
Das Buch Transportation Energy Data Book Edition 39 liefert Daten für den Zusammenhang zwischen Geschwindigkeit und Benzinverbrauch: https://tedb.ornl.gov/wp-content/uploads/2021/02/TEDB_Ed_39.pdf#page=136
Diese werden hier abgeschrieben und in der Datentabelle TEBD hinterlegt:
TEBD <- data.frame(
mpg = c(24.4, 27.9, 30.5, 31.7, 31.2, 31.0, 31.6,
32.4, 32.4, 31.4, 29.2, 26.8, 24.8),
mph = seq(from = 15, to= 75, by = 5)
)
# Datenstruktur
str(TEBD)## 'data.frame': 13 obs. of 2 variables:
## $ mpg: num 24.4 27.9 30.5 31.7 31.2 31 31.6 32.4 32.4 31.4 ...
## $ mph: num 15 20 25 30 35 40 45 50 55 60 ...# Obere 6 Beobachtungen
head(TEBD)## mpg mph
## 1 24.4 15
## 2 27.9 20
## 3 30.5 25
## 4 31.7 30
## 5 31.2 35
## 6 31.0 402 Beschreibung des Datensatzes
2.1 Fragen
Handelt es sich um Daten von aktuellen Fahrzeugen? Die Daten kommen von Autos aus dem Jahr 1997.
Sind es die Verbrauchsdaten eines Fahrzeugs? Nein, von 9 Fahrzeugen.
2.2 Umrechnung
Die Daten liegen im amerikanischen Messsystem vor: miles per gallon (mpg) und miles per hour (mph).
Zur besseren Lesbarkeit sollten wir diese in die uns bekannten Einheiten umrechnen. Eine Meile entspricht 1.609344 km, eine (amerikanische) Gallone 3.785411784 l:
TEBD <-
TEBD %>%
mutate(kmh = mph * 1.609344) %>%
mutate(l100km = (100 * 3.785411784) / (1.609344 * mpg))3 Zusammenhang Geschwindigkeit und Verbrauch
3.1 Linearität des Zusammenhangs
- Ist der Zusammenhang zwischen
l100kmundmpglinear? Nein: \(l100km = \frac{(100 * 3.785411784)}{(1.609344 * mpg)}\)
Korrelation mit Streudiagramm:
plot1 <-
TEBD %>%
cor_test("kmh", "l100km") %>%
plot()
plot1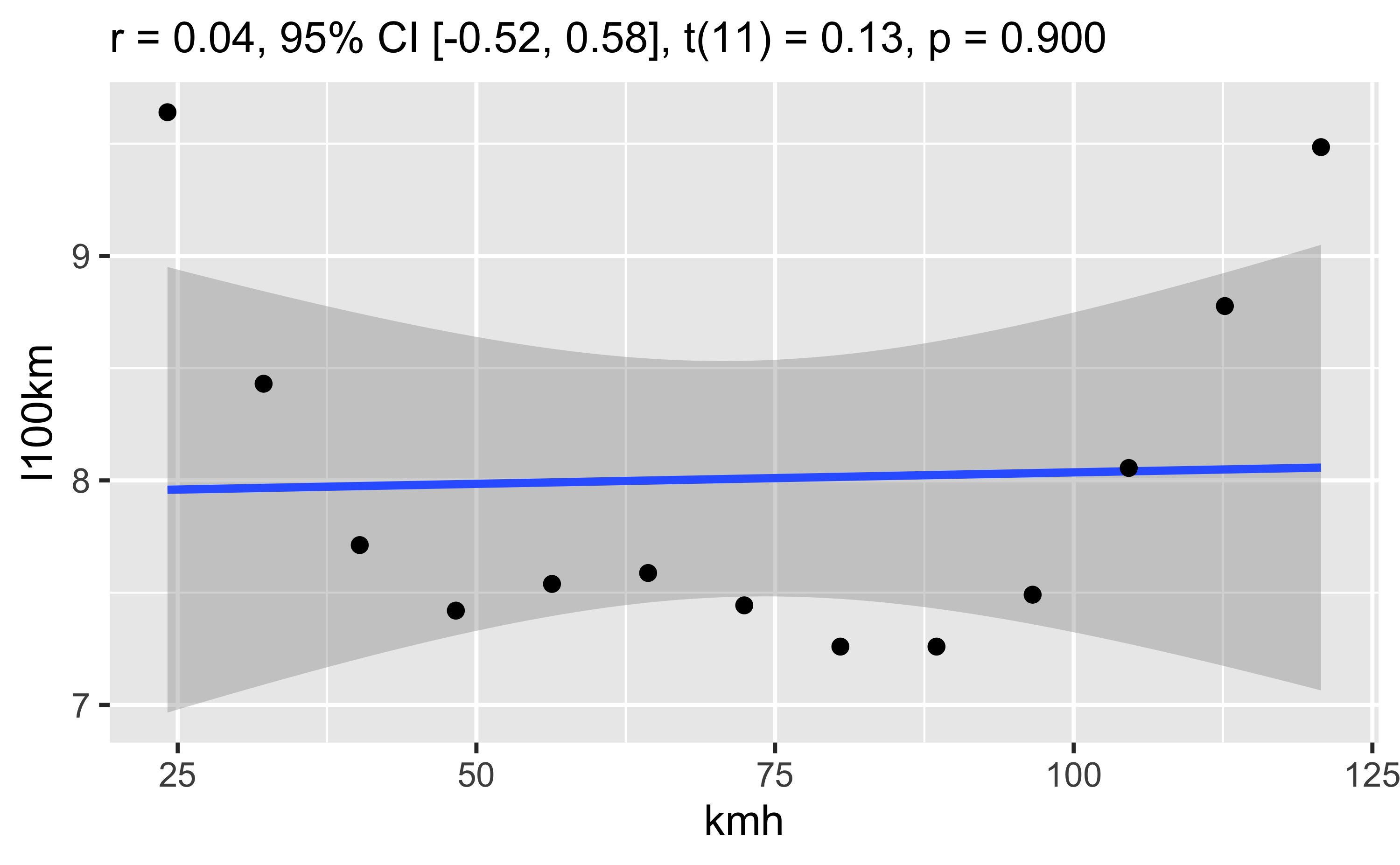
Wie man sieht, gibt es (praktisch) keinen linearen Zusammenhang zwischen den beiden Variablen.
So kann man die Korrelation auch berechnen:
TEBD %>%
select(kmh, l100km) %>%
correlation()## # Correlation Matrix (pearson-method)
##
## Parameter1 | Parameter2 | r | 95% CI | t(11) | p
## --------------------------------------------------------------
## kmh | l100km | 0.04 | [-0.52, 0.58] | 0.13 | 0.900
##
## p-value adjustment method: Holm (1979)
## Observations: 13TEBD %>%
select(kmh, l100km) %>%
correlation() %>%
summary() %>%
plot()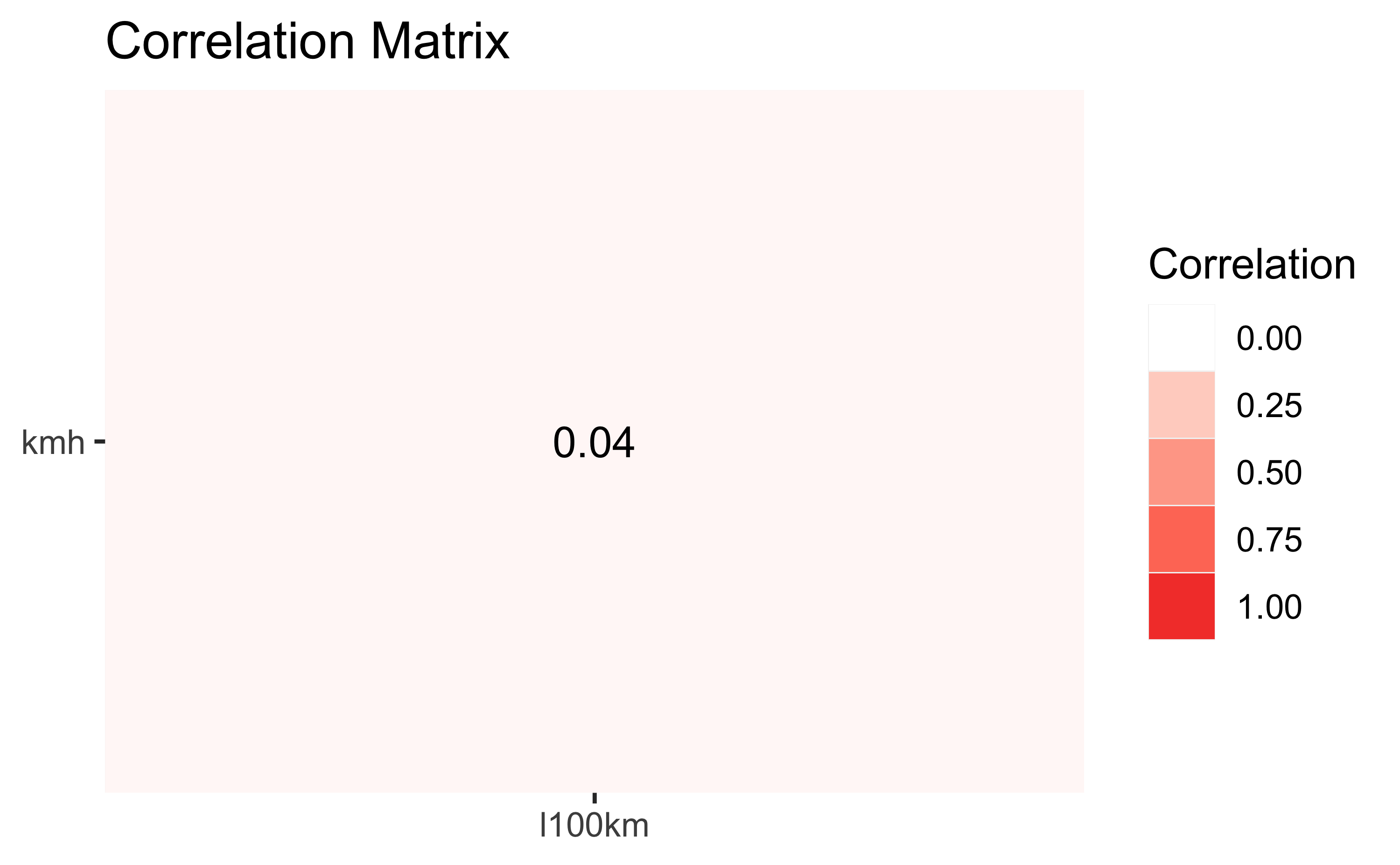
Natürlich gibt es viele Möglichkeiten, die Korrelation (mit R) zu berechnen und zu visualisieren.
3.2 Fragen
- Ist der Zusammenhang zwischen
kmhundl100kmlinear? Nein, eher eine Parabel. - Bei welcher Geschwindigkeit ist der Verbrauch minimal? Zwischen 80 und 90 km/h.
3.3 Verschönern
Fügen wir noch Achsenbeschriftungen und ein anderes “Stylesheet” hinzu:
plot1 +
labs( x = "km/h",
y = "l/100km",
title = "Verbrauch je Geschwindigkeit",
subtitle ="Quelle: Transportation Energy Data Book, Edition 39, Tablle 4.34") +
theme_modern()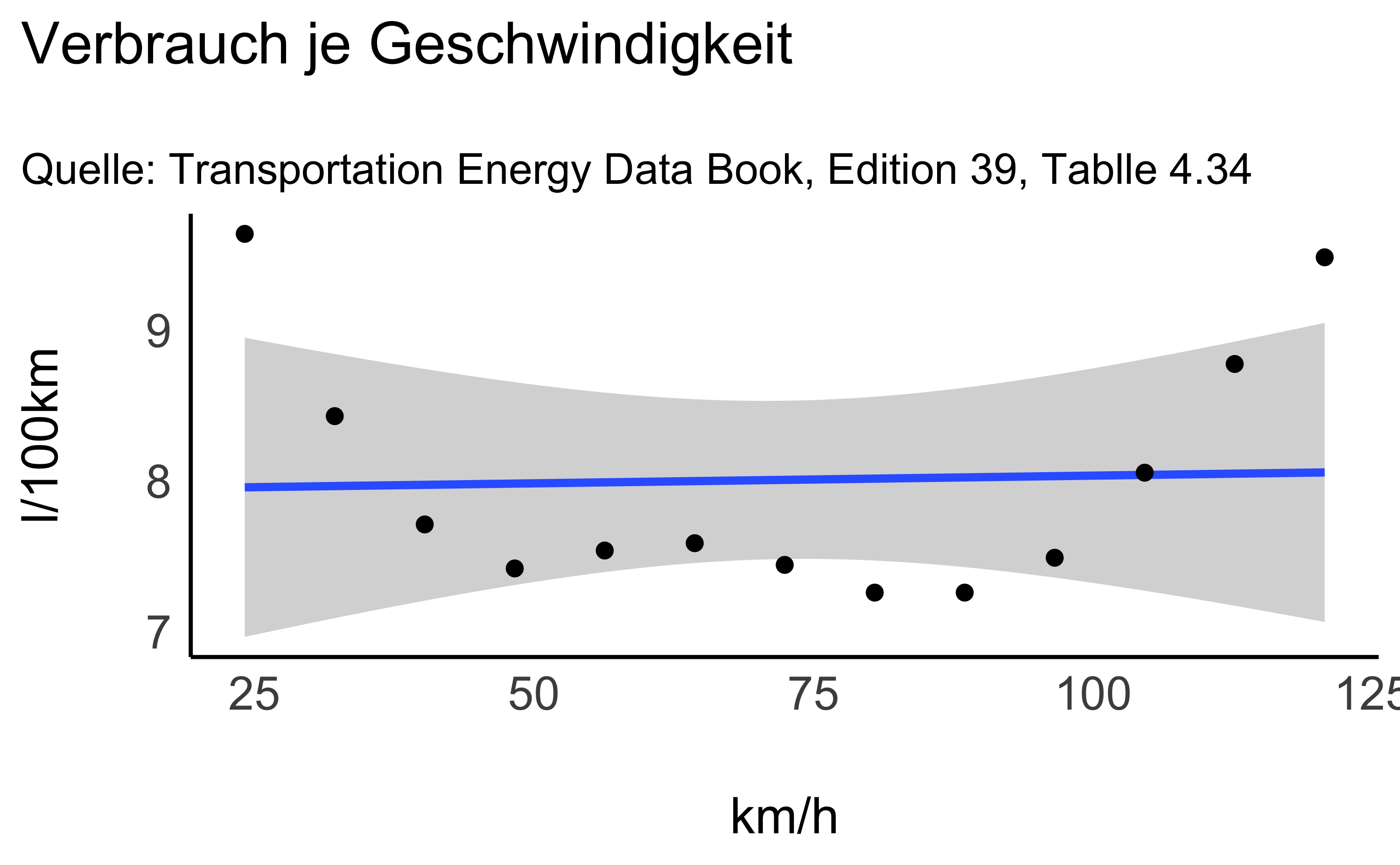
Über ylim() bzw. xlim() können die Achsenskalierung angepasst werden, z.B. die y-Achse so, dass diese bei 0 anfängt und bei 10 aufhört.
plot1 +
labs( x = "km/h",
y = "l/100km",
title = "Verbrauch je Geschwindigkeit",
subtitle ="Quelle: Transportation Energy Data Book, Edition 39, Tablle 4.34") +
ylim(c(0, 10))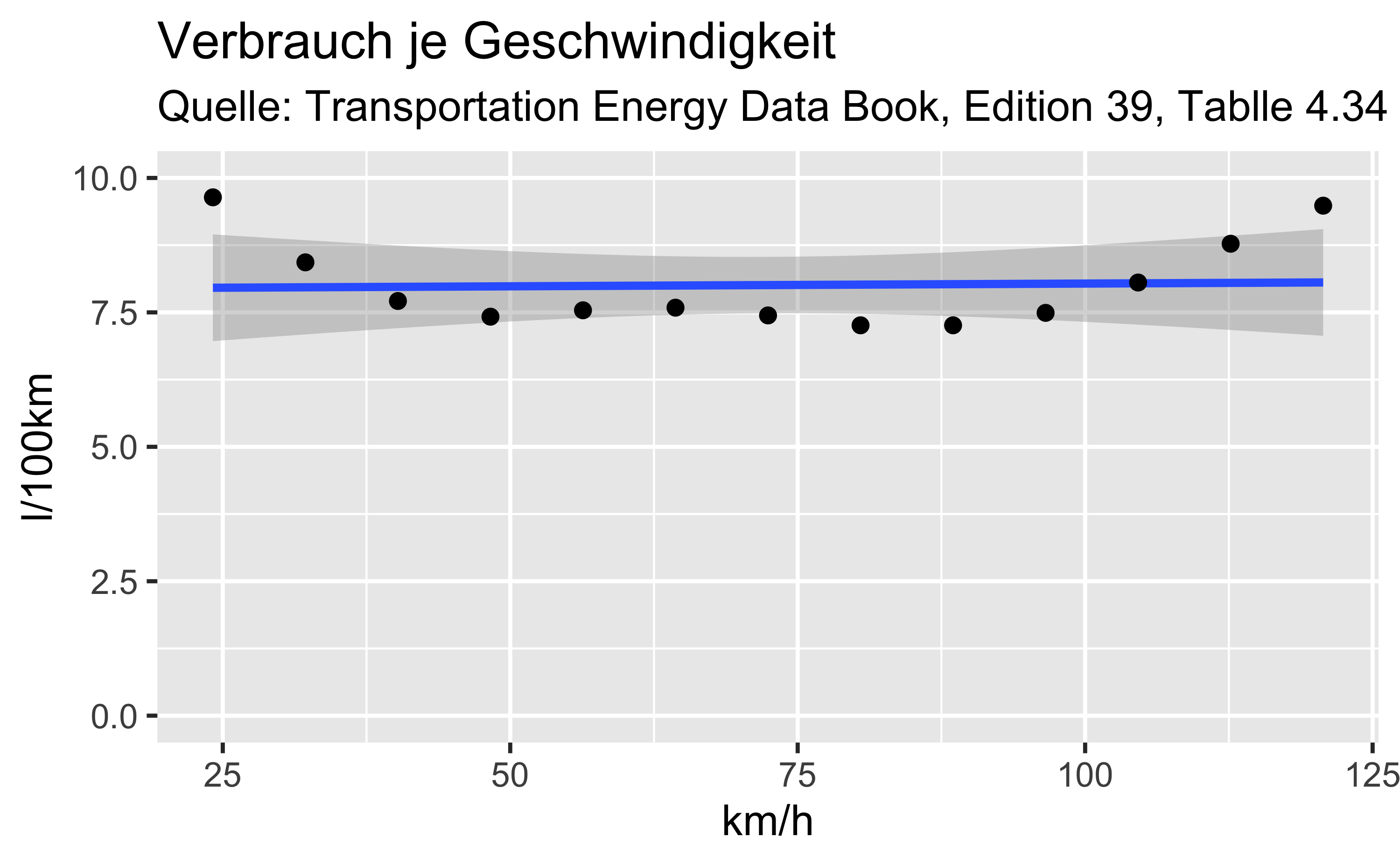
3.4 Vor- und Nachteile der Skalierung
- Welche Vor- und Nachteile hat die Skalierung?
Ohne Skalierung (Beginn bei \(y=0\)) wird suggeriert, dass der Verbauch schon minimal (bei 0 ist), aber die Unterschiede werden deutlicher. Mit Skalierung wird deutlicher erkennbar, dass auch im minimialen Fall über 7l verbraucht werden.
Die Achsenskalierung sollte zielgruppen - und zweckorientiert sein, aber nicht manipulieren.
Achte auf die Achsenskalierung!
4 Verbrauchsdaten
Andreas Wagener hat für ein paar Monate am Ende einer Autofahrt seine Verbrauchsdaten samt Kovariablen (wie z.B. Temperatur) gesammelt und über Kaggle unter der GPL 2 Lizenz veröffentlicht. Für diesen Kurs stehen die Daten unter https://statistix.org/Data/VerbrauchAW.csv:
# URL der Daten
d_url <- "https://statistix.org/Data/VerbrauchAW.csv"
# Daten herunterladen
d <- read_csv2(d_url)Kontrolle der Daten:
# Struktur
str(d)## spec_tbl_df [388 × 12] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
## $ distance : num [1:388] 28 12 11.2 12.9 18.5 8.3 7.8 12.3 4.9 11.9 ...
## $ consume : num [1:388] 5 4.2 5.5 3.9 4.5 6.4 4.4 5 6.4 5.3 ...
## $ speed : num [1:388] 26 30 38 36 46 50 43 40 26 30 ...
## $ temp_inside : num [1:388] 21.5 21.5 21.5 21.5 21.5 21.5 21.5 21.5 21.5 21.5 ...
## $ temp_outside : num [1:388] 12 13 15 14 15 10 11 6 4 9 ...
## $ specials : chr [1:388] NA NA NA NA ...
## $ gas_type : chr [1:388] "E10" "E10" "E10" "E10" ...
## $ AC : num [1:388] 0 0 0 0 0 0 0 0 0 0 ...
## $ rain : num [1:388] 0 0 0 0 0 0 0 0 0 0 ...
## $ sun : num [1:388] 0 0 0 0 0 0 0 0 0 0 ...
## $ refill liters: num [1:388] 45 NA NA NA NA NA NA NA NA NA ...
## $ refill gas : chr [1:388] "E10" NA NA NA ...
## - attr(*, "spec")=
## .. cols(
## .. distance = col_double(),
## .. consume = col_double(),
## .. speed = col_double(),
## .. temp_inside = col_double(),
## .. temp_outside = col_double(),
## .. specials = col_character(),
## .. gas_type = col_character(),
## .. AC = col_double(),
## .. rain = col_double(),
## .. sun = col_double(),
## .. `refill liters` = col_double(),
## .. `refill gas` = col_character()
## .. )
## - attr(*, "problems")=<externalptr># Obere Beobachtungen der Tabelle
head(d)## # A tibble: 6 × 12
## distance consume speed temp_inside temp_outside specials gas_type AC rain
## <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <chr> <dbl> <dbl>
## 1 28 5 26 21.5 12 <NA> E10 0 0
## 2 12 4.2 30 21.5 13 <NA> E10 0 0
## 3 11.2 5.5 38 21.5 15 <NA> E10 0 0
## 4 12.9 3.9 36 21.5 14 <NA> E10 0 0
## 5 18.5 4.5 46 21.5 15 <NA> E10 0 0
## 6 8.3 6.4 50 21.5 10 <NA> E10 0 0
## # … with 3 more variables: sun <dbl>, `refill liters` <dbl>, `refill gas` <chr>4.1 Fragen zum Datensatz
- Handelt es sich um eine Beobachtungsstudie oder um ein randomisiertes Experiment? Beobachtungsstudie
- Was ist hier eine Beobachtungseinheit? Eine Fahrt
- Wie viele Beobachtungen liegen vor? 388
- Wie viele Variablen liegen vor? 12
- Welches Skalenniveau hat die Variable
consume(angegebener Verbrauch in l/100km)? Metrisch-Verhältnisskaliert
- Welches Skalenniveau hat die Variable
AC(Klimaanlage)? Nominal mit 2 Ausprägungen (1: an, 0: aus)
4.2 Beschreibung des Datensatzes
d_describe <- d %>%
select(consume) %>%
describe_distribution()
d_describe## Variable | Mean | SD | IQR | Range | Skewness | Kurtosis | n | n_Missing
## ------------------------------------------------------------------------------------
## consume | 4.91 | 1.03 | 1 | [3.30, 12.20] | 2.94 | 14.49 | 388 | 0Ein Histogramm visualisiert die Verteilung der von Andreas Wagener bei seinen Fahrten realisierten Verbräuche:
describe_distribution(d$consume) %>%
plot()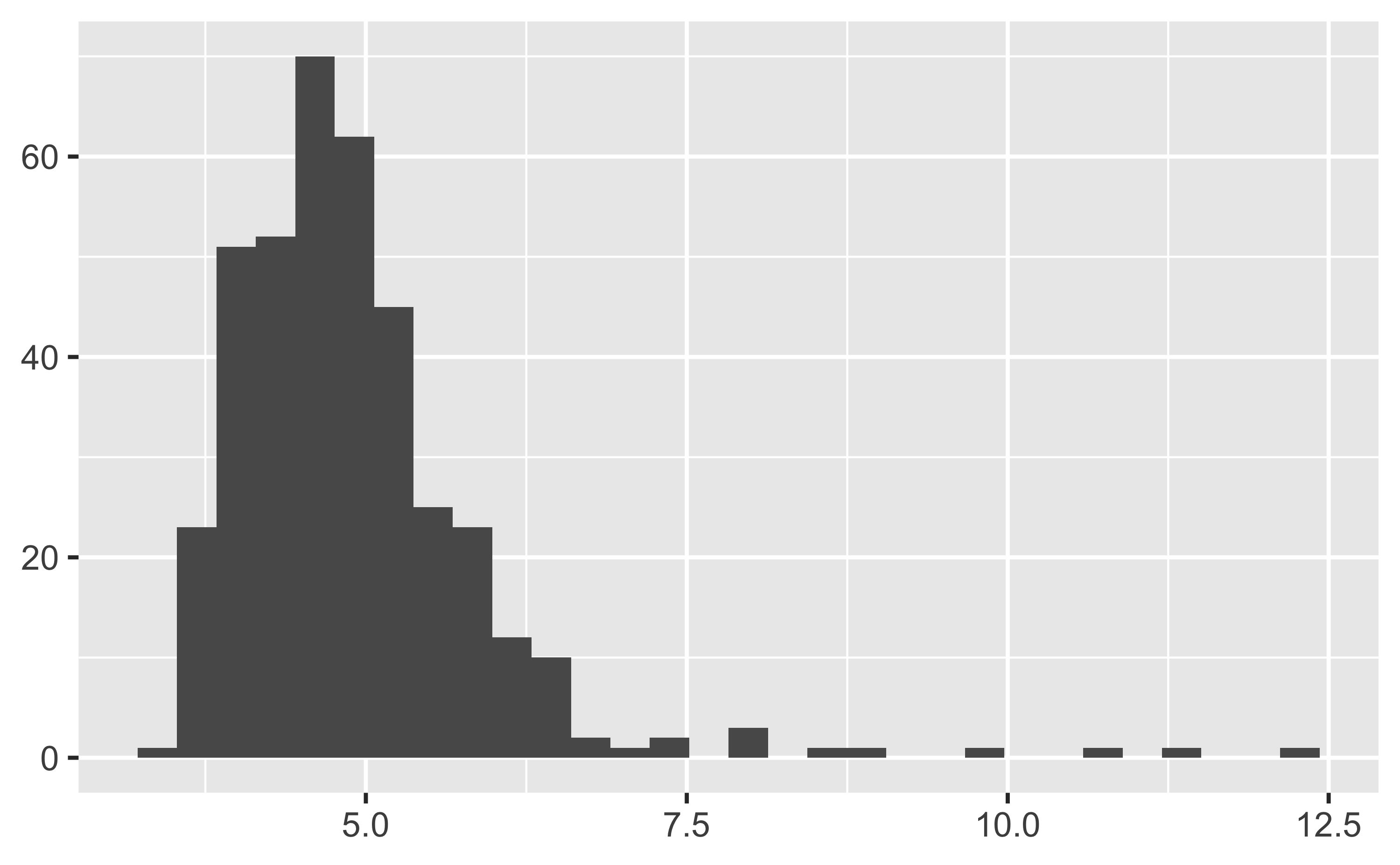
4.2.1 Interpretation der Verteilung
- Was können Sie dem Histogramm entnehmen?
Am häufigsten liegt der Verbrauch zwischen 4 und 5 l/100km. Selten liegt der Verbrauch über 8 l/100km. Es gibt häufig vergleichsweise niedrige Verbräuche, selten relativ hohe, d.h. die Verteilung ist rechtschief (linkssteil). Es gibt nur einen Schwerpunkt, d.h. die Verteilung ist unimodal.
4.3 Empirische Verteilungsfunktion
Berechnen wir den Anteil p mit einem Verbrauch nicht größer als q, d.h. den Wert der empirischen Verteilungsfunktion \(F_n\), den Wert also der dem Anteil der Fahrten entspricht, in denen der Verbrauch z.B. kleiner oder gleich q = 10l war:
d %>%
count(consume <= 10) %>%
mutate(prop = n / sum(n))## # A tibble: 2 × 3
## `consume <= 10` n prop
## <lgl> <int> <dbl>
## 1 FALSE 3 0.00773
## 2 TRUE 385 0.9924.3.1 Fragen
Ändern Sie den Code so, dass Sie die folgenden Fragen beantworten können.
d %>%
count(consume <= 10) %>%
mutate(prop = n / sum(n))## # A tibble: 2 × 3
## `consume <= 10` n prop
## <lgl> <int> <dbl>
## 1 FALSE 3 0.00773
## 2 TRUE 385 0.992- Wie hoch ist der Anteil der Fahren mit einem Verbrauch kleiner gleich 5l?
d %>%
count(consume <= 5) %>%
mutate(prop = n / sum(n))## # A tibble: 2 × 3
## `consume <= 5` n prop
## <lgl> <int> <dbl>
## 1 FALSE 129 0.332
## 2 TRUE 259 0.668Er schafft es in ca. 67% seiner Fahrten einen Verbrauch unter 5l/100km zu erreichen.
- Wie hoch ist der Anteil der Fahren mit einem Verbrauch größer als 7.5l?
d %>%
count(consume > 7.5) %>%
mutate(prop = n / sum(n))## # A tibble: 2 × 3
## `consume > 7.5` n prop
## <lgl> <int> <dbl>
## 1 FALSE 379 0.977
## 2 TRUE 9 0.02324.4 Quantile der empirischen Verteilung
Suchen wir das 5%-Quantil der “Verbrauch-Verteilung”, den Wert also, der von 5% der Verbrauchswerte aller Fahrten nicht übertroffen wird.
Dazu berechnen wir die kumulierte (Häufigkeits-)Verteilung:
d <-
d %>%
mutate(consume_cume_dist = cume_dist(consume))Das sieht so aus:
d %>%
ggplot(aes(x = consume, y = consume_cume_dist)) +
geom_line()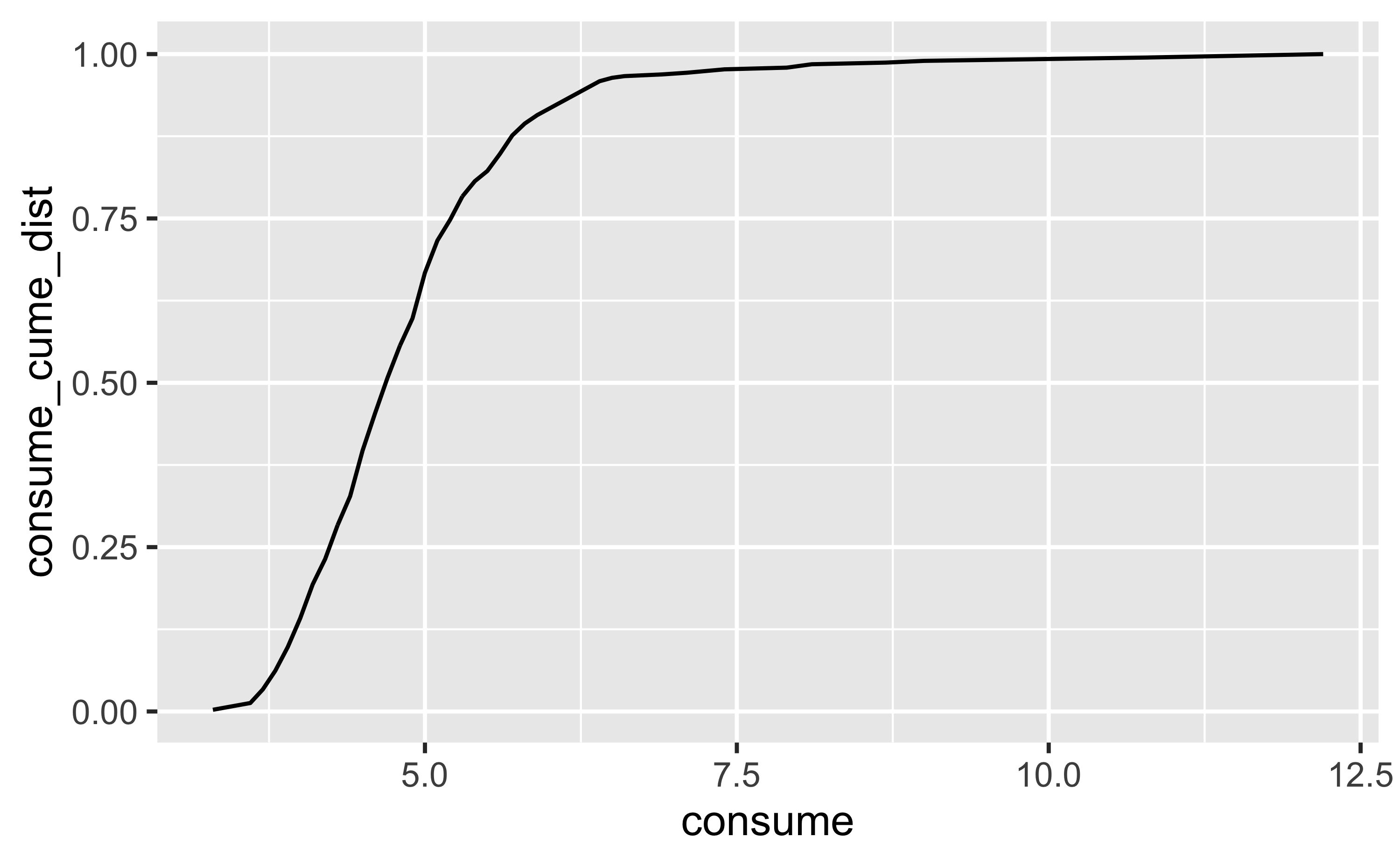
Jetzt ziehen wir die Zeile, bei der consume_cume_dist==.05,
bzw. der größte Wert unter dieser Grenze:
d %>%
filter(consume_cume_dist < .05) %>%
summarise(max(consume))## # A tibble: 1 × 1
## `max(consume)`
## <dbl>
## 1 3.7In 5% seiner Fahrten lag der Verbrauch bei ca. 3,7l - oder darunter.
Ändern Sie den Code so, dass Sie die folgende Frage beantworten können.
4.5 Frage
- Mit welchem (maximalem) Verbrauch kam Andreas Wagener in 80% seiner Fahren zurecht?
d %>%
filter(consume_cume_dist < .80) %>%
pull(consume) %>%
max()## [1] 5.3In 80% seiner Fahrten kam er mit 5.4l/100km - oder weniger hin.
Merke: Die empirische Verteilungsfunktion \(F_n(X)\) zeigt die kumulierte (relative) Häufigkeit eines Merkmals \(X\).
5 Überblick über die Verteilung
describe_distribution() liefert einen Überblick über die gängigen Kennzahlen einer metrischen Variable:
d %>%
select(consume) %>%
describe_distribution()## Variable | Mean | SD | IQR | Range | Skewness | Kurtosis | n | n_Missing
## ------------------------------------------------------------------------------------
## consume | 4.91 | 1.03 | 1 | [3.30, 12.20] | 2.94 | 14.49 | 388 | 05.1 Fragen
- Wie hoch ist der durchschnittliche Verbrauch? 4.9
- Wie groß ist der Median? 4.7
- In welchen Bereich liegen 50% der Verbräuche? min-median, also 3.3 bis 4.7; Q1 bis Q3 (die mittleren 50%), also 4.3 bs 5.3; und median bis max, also 4.7 bis 5.3 (jeweils einschließlich)
- In der Datentabelle liegen außerdem noch die Innentemperatur (
temp_inside) sowie die Außentemperatur vor (temp_outside). Beim welcher Temperatur wird die Streuung größer sein?temp_outside
d %>%
select(temp_outside, temp_inside) %>%
describe_distribution()## Variable | Mean | SD | IQR | Range | Skewness | Kurtosis | n | n_Missing
## ------------------------------------------------------------------------------------------
## temp_outside | 11.36 | 6.99 | 9 | [-5.00, 31.00] | 0.57 | -0.02 | 388 | 0
## temp_inside | 21.93 | 1.01 | 1 | [19.00, 25.50] | 0.99 | 2.80 | 376 | 126 Klimaanlage
Vergleichen wir den Verbrauch bei Fahrt mit vs. ohne Klimananlage.
Die Variable AC muss aber zunächst als kategoriale Variable definiert werden.
d <-
d %>%
mutate(AC_f = case_when(AC == 0 ~ "Nein",
AC == 1 ~ "Ja"))lm1 <- lm(consume ~ AC_f, data = d)estimate_means(lm1)## Estimated Marginal Means
##
## AC_f | Mean | SE | 95% CI
## ---------------------------------
## Nein | 4.88 | 0.05 | [4.78, 4.99]
## Ja | 5.26 | 0.19 | [4.89, 5.63]
##
## Marginal means estimated at AC_fPlotten wir den Unterschied:
estimate_means(lm1) %>%
plot() 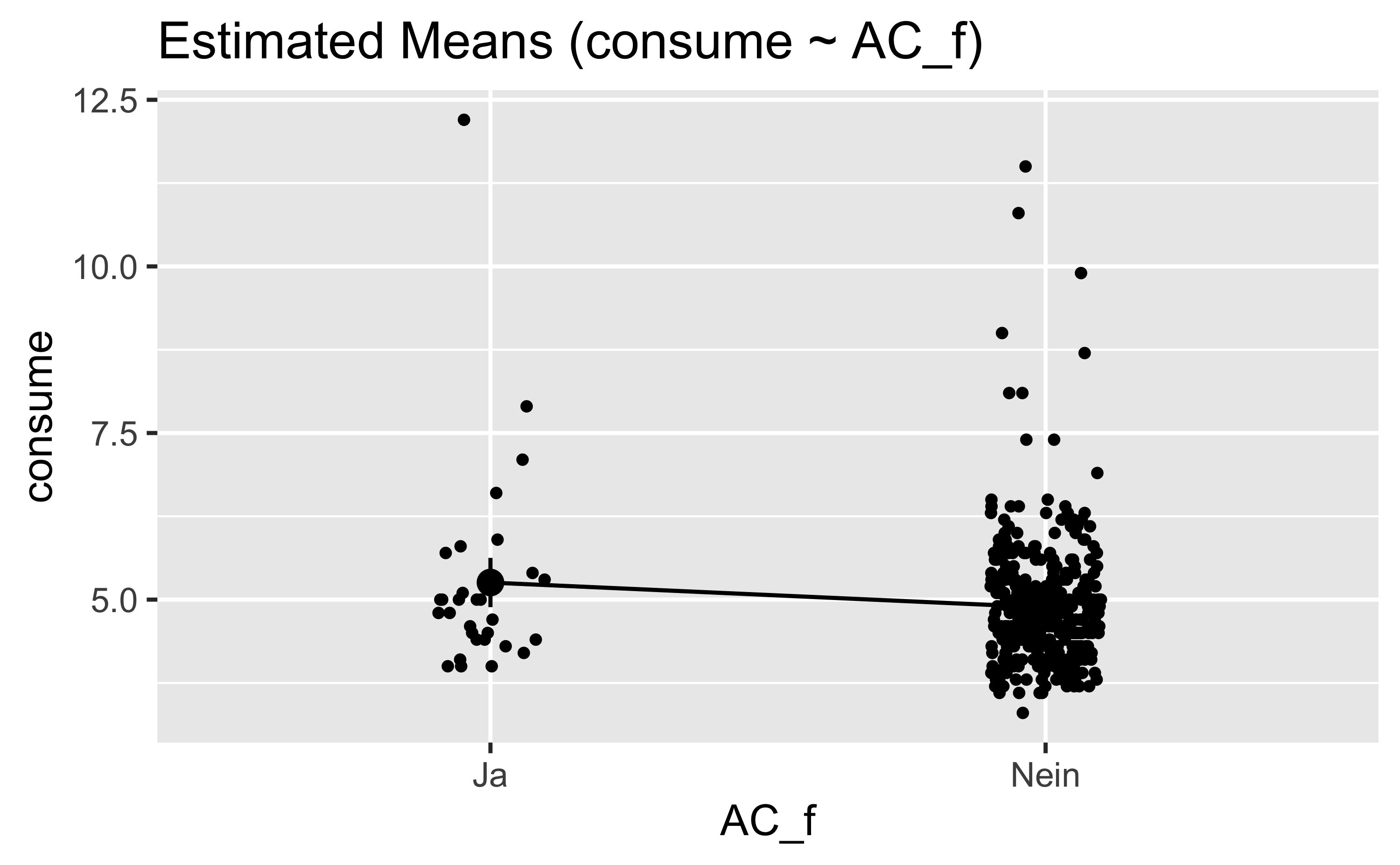
Sieht nicht so schön aus. Probieren wir es so:
ggplot(d, aes(x = AC_f, y = consume, fill = AC_f)) +
geom_violin() +
geom_jitter2() +
theme_modern()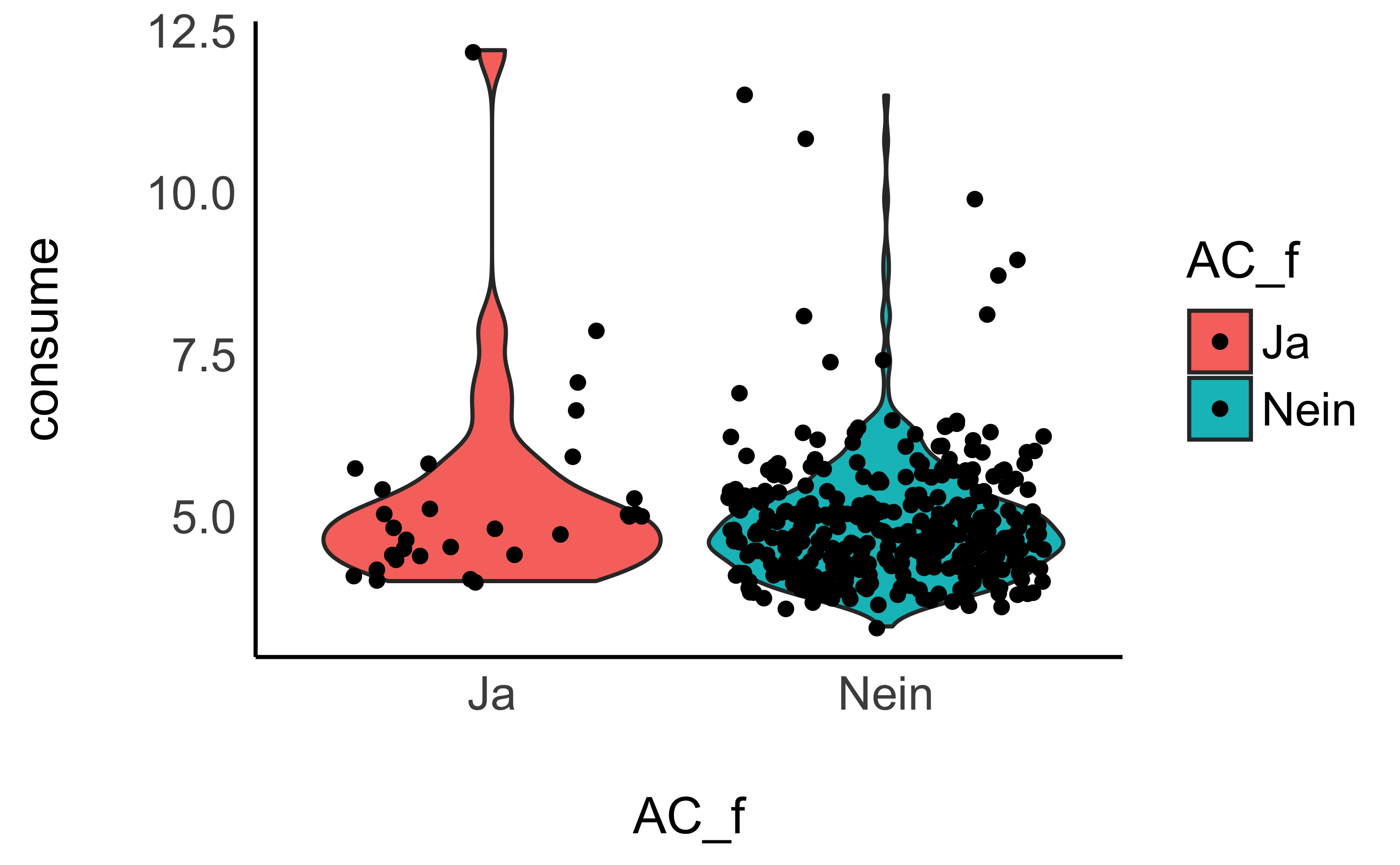
Oder mit Boxplot:
ggplot(d, aes(x = AC_f, y = consume, fill = AC_f)) +
geom_boxplot() +
geom_jitter(alpha = .3, width = .2) +
theme_modern()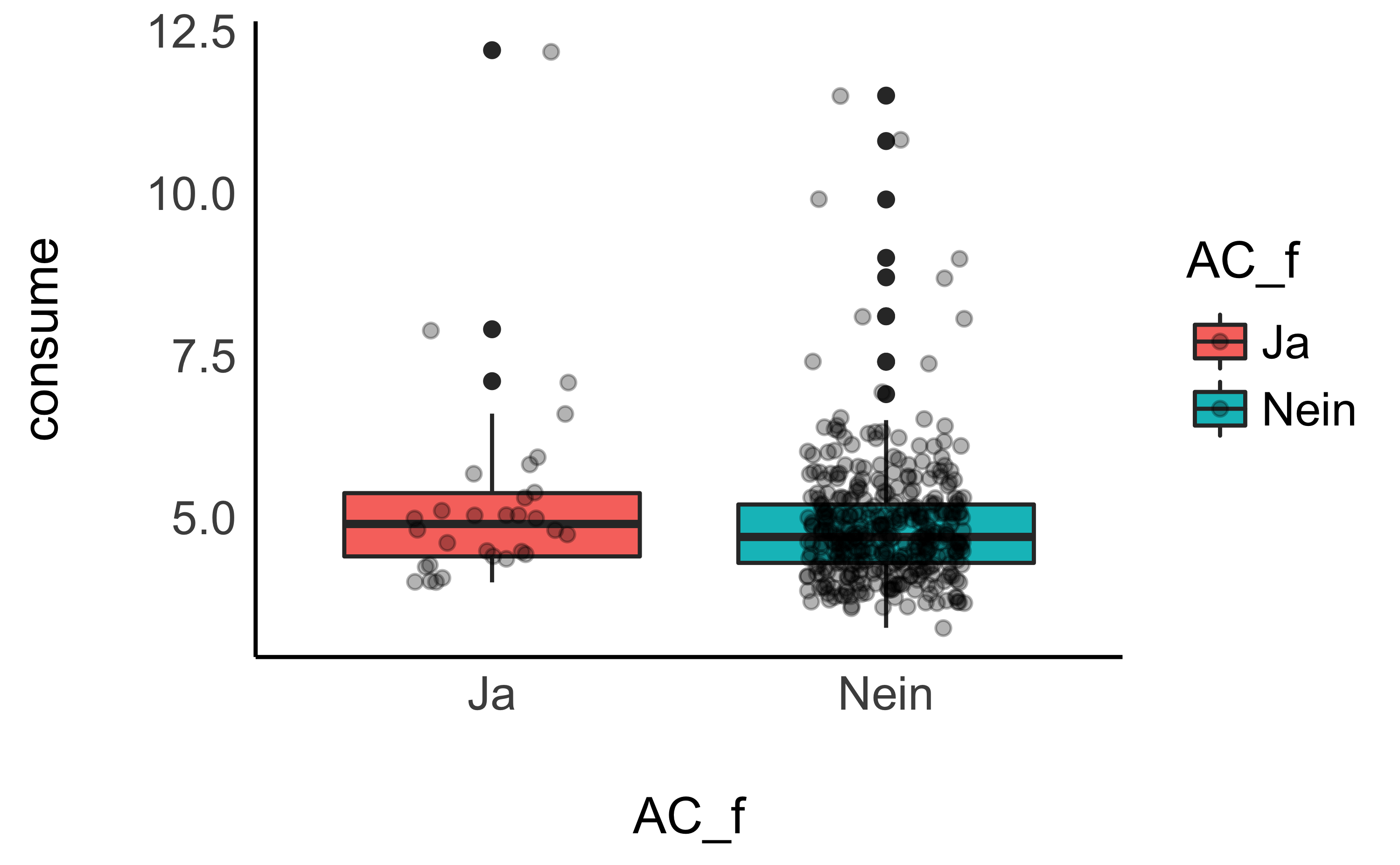
6.1 Frage
- Was können Sie über eine Vergleich der Verteilungen der der Verbräuche mit und ohne Klimaanlage aussagen?
So wohl im Diagramm, als auch in den Kennzahlen (z.B. Median (median), aber auch arithmetischer Mittelwert (mean)), ist zu erkennen, dass die Verteilung des Verbrauchs in l/100km höher ist, wenn die Klimaanlage an ist.
In beiden Gruppen gibt es Ausreißer nach oben.
7 Geschwindigkeit und Verbrauch
Berechnen wir die Korrelation (zur Erinnerung, eine Kennzahl zum linearen Zusammenhang).
d %>%
cor_test("consume", "speed") ## Parameter1 | Parameter2 | r | 95% CI | t(386) | p
## ---------------------------------------------------------------------
## consume | speed | -0.23 | [-0.32, -0.13] | -4.60 | < .001***
##
## Observations: 388Oder eine Korrelationsmatrix, also alle Korrelationen von mehreren Variablen:
d %>%
select(consume, speed, distance) %>%
correlation()## # Correlation Matrix (pearson-method)
##
## Parameter1 | Parameter2 | r | 95% CI | t(386) | p
## ---------------------------------------------------------------------
## consume | speed | -0.23 | [-0.32, -0.13] | -4.60 | < .001***
## consume | distance | -0.13 | [-0.23, -0.03] | -2.56 | 0.011*
## speed | distance | 0.56 | [ 0.49, 0.63] | 13.36 | < .001***
##
## p-value adjustment method: Holm (1979)
## Observations: 388Streudiagram::
d %>%
cor_test("consume", "speed") %>%
plot()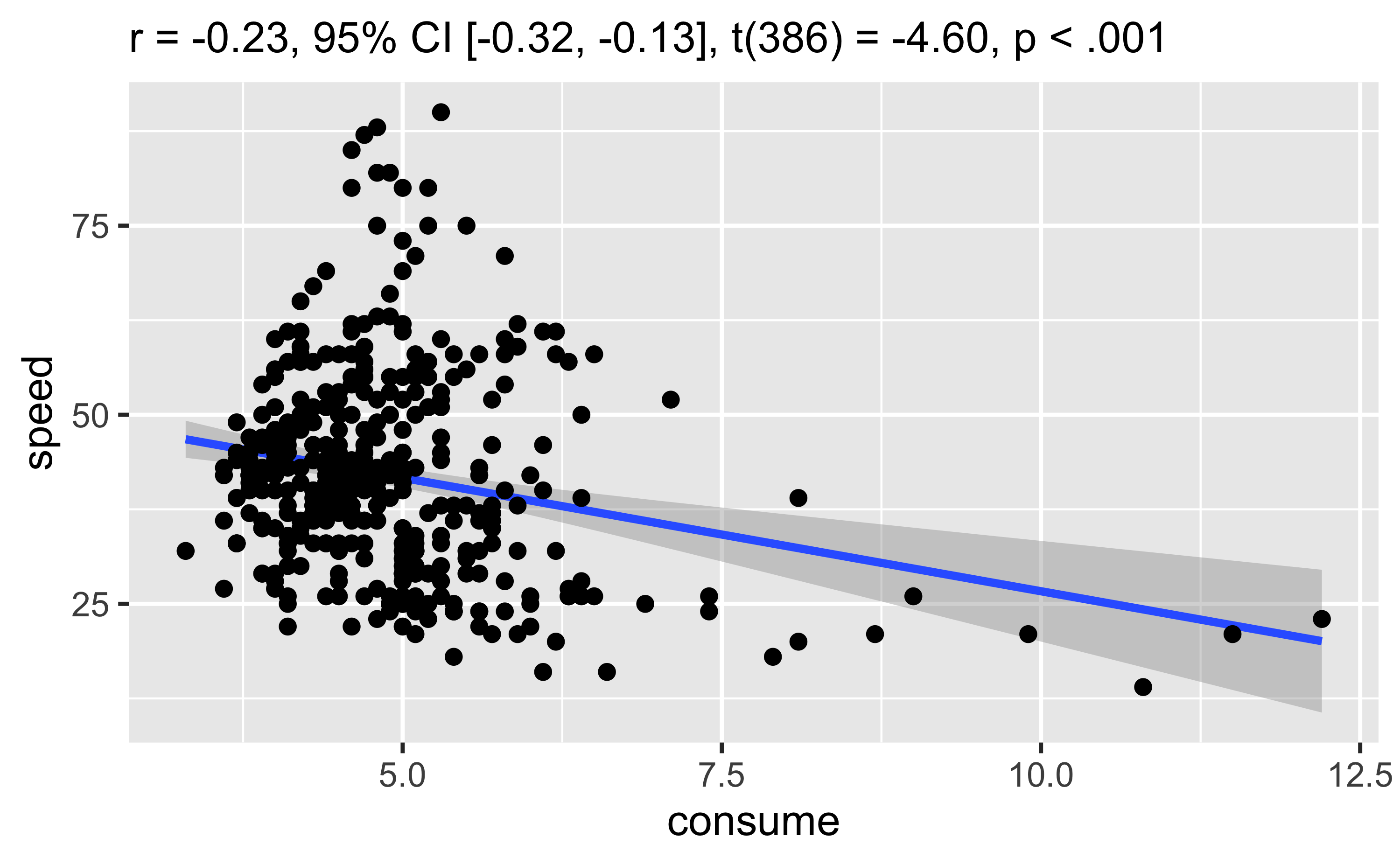
7.1 Frage
- Was ist zu beachten, wenn in dieser Datentabelle der Zusammenhang zwischen
consumeundspeedanalysiert wird?
Es handelt sich um die Durchschnittswerte der Variablen. So kann es bei niedrigen Durchschnittsgeschwindigkeiten z.B. sein, das häufig gebremst und beschleunigt wurde, was den Spritverbrauch erhöht. Bei hohen Durchschnittsgeschwindigkeiten konnte vielleicht gleichmäßiger gefahren werden. D.h., hier können viele Kovariablen das Bild verzerren.
Der Korrelationskoeffizient \(r\) misst nur lineare Zusammenhänge, im Streudiagramm ist aber zu erkennen dass der Zusammenhang hier nicht linear ist - siehe auch die TEBD-Auswertung oben.
8 Your-Turn
Analysieren Sie den Zusammenhang zwischen consume und einer weiteren Kovariable. Was stellen Sie fest?
9 Reproduzierbarkeit
## ─ Session info ───────────────────────────────────────────────────────────────────────────────────────────────────────
## setting value
## version R version 4.1.3 (2022-03-10)
## os macOS Big Sur/Monterey 10.16
## system x86_64, darwin17.0
## ui X11
## language (EN)
## collate en_US.UTF-8
## ctype en_US.UTF-8
## tz Europe/Berlin
## date 2022-05-02
##
## ─ Packages ───────────────────────────────────────────────────────────────────────────────────────────────────────────
## package * version date lib source
## assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.1.0)
## backports 1.4.1 2021-12-13 [1] CRAN (R 4.1.0)
## bayestestR * 0.11.5 2021-10-30 [1] CRAN (R 4.1.0)
## bit 4.0.4 2020-08-04 [2] CRAN (R 4.1.0)
## bit64 4.0.5 2020-08-30 [2] CRAN (R 4.1.0)
## blogdown 1.8 2022-02-16 [2] CRAN (R 4.1.2)
## bookdown 0.24.2 2021-10-15 [1] Github (rstudio/bookdown@ba51c26)
## brio 1.1.3 2021-11-30 [1] CRAN (R 4.1.0)
## broom 0.7.12 2022-01-28 [1] CRAN (R 4.1.2)
## bslib 0.3.1 2021-10-06 [1] CRAN (R 4.1.0)
## cachem 1.0.6 2021-08-19 [1] CRAN (R 4.1.0)
## callr 3.7.0 2021-04-20 [1] CRAN (R 4.1.0)
## cellranger 1.1.0 2016-07-27 [1] CRAN (R 4.1.0)
## cli 3.2.0 2022-02-14 [1] CRAN (R 4.1.2)
## coda 0.19-4 2020-09-30 [1] CRAN (R 4.1.0)
## colorout * 1.2-2 2022-01-04 [1] Github (jalvesaq/colorout@79931fd)
## colorspace 2.0-3 2022-02-21 [1] CRAN (R 4.1.2)
## correlation * 0.8.0.1 2022-04-21 [1] https://easystats.r-universe.dev (R 4.1.3)
## crayon 1.5.1 2022-03-26 [1] CRAN (R 4.1.2)
## curl 4.3.2 2021-06-23 [1] CRAN (R 4.1.0)
## datawizard * 0.4.0.9 2022-04-21 [1] https://easystats.r-universe.dev (R 4.1.3)
## DBI 1.1.2 2021-12-20 [1] CRAN (R 4.1.0)
## dbplyr 2.1.1 2021-04-06 [1] CRAN (R 4.1.0)
## desc 1.4.0 2021-09-28 [1] CRAN (R 4.1.0)
## devtools 2.4.3 2021-11-30 [1] CRAN (R 4.1.0)
## digest 0.6.29 2021-12-01 [1] CRAN (R 4.1.0)
## dplyr * 1.0.8 2022-02-08 [1] CRAN (R 4.1.2)
## easystats * 0.4.3 2022-04-21 [1] https://easystats.r-universe.dev (R 4.1.3)
## effectsize * 0.6.0.1 2022-01-26 [1] CRAN (R 4.1.2)
## ellipsis 0.3.2 2021-04-29 [1] CRAN (R 4.1.0)
## emmeans 1.7.2 2022-01-04 [1] CRAN (R 4.1.2)
## estimability 1.3 2018-02-11 [1] CRAN (R 4.1.0)
## evaluate 0.14 2019-05-28 [1] CRAN (R 4.1.0)
## fansi 1.0.3 2022-03-24 [1] CRAN (R 4.1.2)
## farver 2.1.0 2021-02-28 [1] CRAN (R 4.1.0)
## fastmap 1.1.0 2021-01-25 [2] CRAN (R 4.1.0)
## forcats * 0.5.1 2021-01-27 [1] CRAN (R 4.1.0)
## fs 1.5.2 2021-12-08 [1] CRAN (R 4.1.0)
## generics 0.1.2 2022-01-31 [1] CRAN (R 4.1.2)
## ggplot2 * 3.3.5 2021-06-25 [2] CRAN (R 4.1.0)
## glue 1.6.2 2022-02-24 [1] CRAN (R 4.1.2)
## gtable 0.3.0 2019-03-25 [1] CRAN (R 4.1.0)
## haven 2.4.3 2021-08-04 [1] CRAN (R 4.1.0)
## highr 0.9 2021-04-16 [1] CRAN (R 4.1.0)
## hms 1.1.1 2021-09-26 [1] CRAN (R 4.1.0)
## htmltools 0.5.2 2021-08-25 [1] CRAN (R 4.1.0)
## httr 1.4.2 2020-07-20 [1] CRAN (R 4.1.0)
## insight * 0.17.0.4 2022-04-20 [1] https://easystats.r-universe.dev (R 4.1.3)
## jquerylib 0.1.4 2021-04-26 [1] CRAN (R 4.1.0)
## jsonlite 1.7.3 2022-01-17 [1] CRAN (R 4.1.2)
## knitr 1.37 2021-12-16 [1] CRAN (R 4.1.0)
## labeling 0.4.2 2020-10-20 [1] CRAN (R 4.1.0)
## lattice 0.20-45 2021-09-22 [2] CRAN (R 4.1.3)
## lifecycle 1.0.1 2021-09-24 [1] CRAN (R 4.1.0)
## lubridate 1.8.0 2021-10-07 [1] CRAN (R 4.1.0)
## magrittr 2.0.3 2022-03-30 [1] CRAN (R 4.1.2)
## Matrix 1.4-0 2021-12-08 [2] CRAN (R 4.1.3)
## memoise 2.0.0 2021-01-26 [2] CRAN (R 4.1.0)
## mgcv 1.8-39 2022-02-24 [2] CRAN (R 4.1.3)
## modelbased * 0.8.0 2022-04-12 [1] https://easystats.r-universe.dev (R 4.1.3)
## modelr 0.1.8 2020-05-19 [1] CRAN (R 4.1.0)
## munsell 0.5.0 2018-06-12 [1] CRAN (R 4.1.0)
## mvtnorm 1.1-3 2021-10-08 [1] CRAN (R 4.1.0)
## nlme 3.1-155 2022-01-16 [2] CRAN (R 4.1.3)
## parameters * 0.17.0.9 2022-04-20 [1] https://easystats.r-universe.dev (R 4.1.3)
## performance * 0.9.0.2 2022-04-20 [1] https://easystats.r-universe.dev (R 4.1.3)
## pillar 1.7.0 2022-02-01 [1] CRAN (R 4.1.2)
## pkgbuild 1.2.0 2020-12-15 [2] CRAN (R 4.1.0)
## pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.1.0)
## pkgload 1.2.4 2021-11-30 [1] CRAN (R 4.1.0)
## prettyunits 1.1.1 2020-01-24 [1] CRAN (R 4.1.0)
## processx 3.5.2 2021-04-30 [1] CRAN (R 4.1.0)
## ps 1.6.0 2021-02-28 [1] CRAN (R 4.1.0)
## purrr * 0.3.4 2020-04-17 [1] CRAN (R 4.1.0)
## R6 2.5.1 2021-08-19 [1] CRAN (R 4.1.0)
## Rcpp 1.0.8.3 2022-03-17 [1] CRAN (R 4.1.2)
## readr * 2.1.2 2022-01-30 [1] CRAN (R 4.1.2)
## readxl 1.3.1 2019-03-13 [1] CRAN (R 4.1.0)
## remotes 2.4.0 2021-06-02 [2] CRAN (R 4.1.0)
## report * 0.5.1.1 2022-04-11 [1] https://easystats.r-universe.dev (R 4.1.3)
## reprex 2.0.1 2021-08-05 [1] CRAN (R 4.1.0)
## rlang 1.0.2 2022-03-04 [1] CRAN (R 4.1.2)
## rmarkdown 2.11 2021-09-14 [1] CRAN (R 4.1.0)
## rprojroot 2.0.2 2020-11-15 [2] CRAN (R 4.1.0)
## rstudioapi 0.13 2020-11-12 [1] CRAN (R 4.1.0)
## rvest 1.0.2 2021-10-16 [1] CRAN (R 4.1.0)
## sass 0.4.0 2021-05-12 [1] CRAN (R 4.1.0)
## scales 1.2.0 2022-04-13 [1] CRAN (R 4.1.3)
## see * 0.7.0.1 2022-04-12 [1] https://easystats.r-universe.dev (R 4.1.3)
## sessioninfo 1.1.1 2018-11-05 [2] CRAN (R 4.1.0)
## stringi 1.7.6 2021-11-29 [1] CRAN (R 4.1.0)
## stringr * 1.4.0 2019-02-10 [1] CRAN (R 4.1.0)
## testthat 3.1.2 2022-01-20 [1] CRAN (R 4.1.2)
## tibble * 3.1.6 2021-11-07 [1] CRAN (R 4.1.0)
## tidyr * 1.2.0 2022-02-01 [1] CRAN (R 4.1.2)
## tidyselect 1.1.2 2022-02-21 [1] CRAN (R 4.1.2)
## tidyverse * 1.3.1 2021-04-15 [1] CRAN (R 4.1.0)
## tzdb 0.1.2 2021-07-20 [2] CRAN (R 4.1.0)
## usethis 2.0.1 2021-02-10 [2] CRAN (R 4.1.0)
## utf8 1.2.2 2021-07-24 [1] CRAN (R 4.1.0)
## vctrs 0.4.0 2022-03-30 [1] CRAN (R 4.1.2)
## vroom 1.5.7 2021-11-30 [1] CRAN (R 4.1.0)
## withr 2.5.0 2022-03-03 [1] CRAN (R 4.1.2)
## xfun 0.29 2021-12-14 [1] CRAN (R 4.1.0)
## xml2 1.3.3 2021-11-30 [1] CRAN (R 4.1.0)
## xtable 1.8-4 2019-04-21 [1] CRAN (R 4.1.0)
## yaml 2.2.2 2022-01-25 [1] CRAN (R 4.1.2)
##
## [1] /Users/sebastiansaueruser/Library/R/x86_64/4.1/library
## [2] /Library/Frameworks/R.framework/Versions/4.1/Resources/library