1 R-Pakete
library(tidyverse) # data wrangling
theme_set(theme_minimal()) # Stylesheet für ggplot22 Hintergrund
Will man eine Verteilung untersuchen, sind Verteilungsfunktion und Quantilsfunktion wichtige Größen. Nicht nur für theoretische, sondern auch für empirische Verteilungen kann man diese Funktionen anwenden.
Allerdings ist die Umsetzung in R vielleicht nicht ganz klar. Daher soll dieser Post zeigen, wie man eine empirische Verteilungfunktion und Quantilsfunktion in R berechnet.
3 Verteilungsfunktion der Normalverteilung
Für eine Normalverteilung kann man sich Quantile und Verteilungsfunktion einfach in R ausgeben lassen.
Wert der Verteilungsfunktion bei :
pnorm(q = 0)
#> [1] 0.5Ausgehend von einer Standardnormalverteilung sagt uns R, dass der Wert der Verteilungsfunktion beträgt.
Quantile, z.B. :
qnorm(p = .5)
#> [1] 0Passt!
Das Plotten geht analog:
ggplot(tibble(x = c(-3, 3)), aes(x = x)) +
stat_function(fun = pnorm) +
labs(title = "Verteilungsfunktion F der Normalverteilung")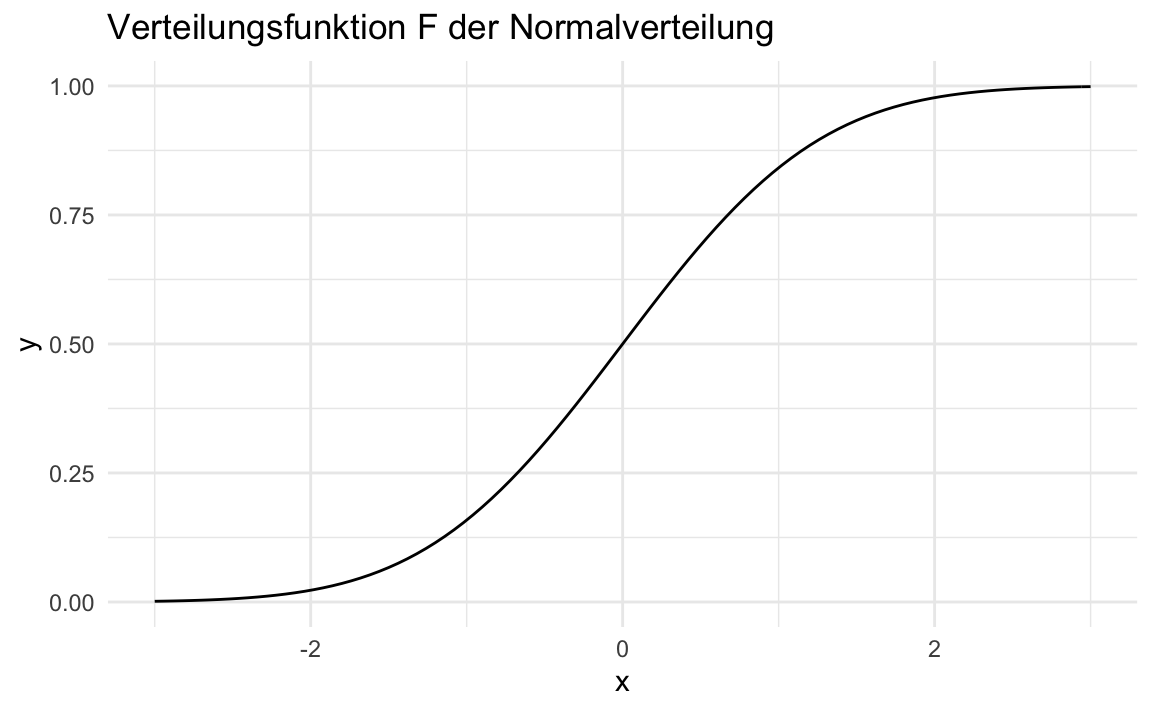
4 Empirische Verteilungsfunktion
Erzeugen wir uns (standard-)normalverteilte Daten:
d_normal <-
tibble(x = rnorm(n = 1e04))4.1 Tidyverse
Die empirische Verteilungsfunktion für kann man, so mit dem Tidyverse bekommen
4.1.1 Tidyverse 1
Dann zählen wir den Anteil der Beobachtungen (Zeilen), die dem gesuchten Wert der Verteilungsfunktion entsprechen, z.B. :
d_normal %>%
count(x <= 0)
#> # A tibble: 2 × 2
#> `x <= 0` n
#> <lgl> <int>
#> 1 FALSE 4951
#> 2 TRUE 5049Also etwa 50%.
4.1.2 Tidyverse 2
So geht es auch, recht umständlich allerdings:
Zunächst erzeugen wir die kumulierte Verteilung.
d_normal <-
d_normal %>%
mutate(x_cume_dist = cume_dist(x))Dann lesen wir den Wert von x_cume_dist an der gewünschten Stelle von x aus:
d_normal %>%
filter(x <= 0) %>%
summarise(max(x_cume_dist))
#> # A tibble: 1 × 1
#> `max(x_cume_dist)`
#> <dbl>
#> 1 0.5054.1.3 Plotten der ECDF
Und so kann man die empirische Verteilungsfunktion plotten, auch genannt empirical cumulative density function (ecdf):
d_normal %>%
ggplot(aes(x = x)) +
stat_ecdf(geom = "step")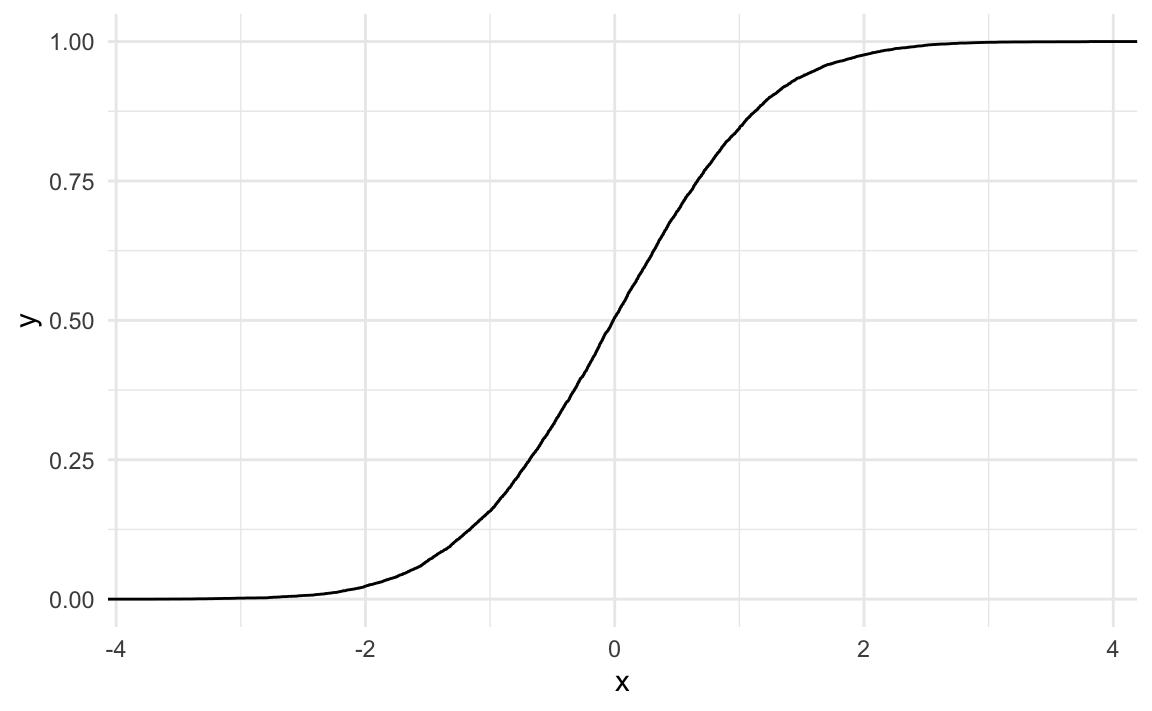
4.1.4 Quantile
Zur Erinnerung: Das -Quantil ist der Wert, der von Prozent der Beobachtungen der Verteilung nicht überschritten wird.
Anschaulich: Wir schneiden den Anteil links von der Verteilung ab, und fragen uns, bei welchem Wert wir die Schere ansetzen müssen.
Quantil für :
d_normal %>%
filter(percent_rank(x) <= .5) %>%
summarise(max(x))
#> # A tibble: 1 × 1
#> `max(x)`
#> <dbl>
#> 1 -0.0110Also etwa Null, passt.
4.2 Base R
4.2.1 Quantile
Mit Base R geht es schön einfach:
quantile(d_normal$x, prob = .5)
#> 50%
#> -0.01070173Oder, etwas mehr Tidyverse-Stil:
d_normal %>%
summarise(x_50perc = quantile(x, prob = .5))
#> # A tibble: 1 × 1
#> x_50perc
#> <dbl>
#> 1 -0.01074.2.2 ECDF
mit ecdf(x) erzeugt man eine Funktion und zwar eine, die die kumulierten Anteile für x wiedergibt:
F <- ecdf(d_normal$x)Wenn einmal definiert, können wir die Funktion bequem befragen.
Hey F, was ist dein Wert bei ?
F(0)
#> [1] 0.504950%! Passt
4.2.3 Plot
ecdf() hat auch eine Plot-Methode:
plot(ecdf(d_normal$x))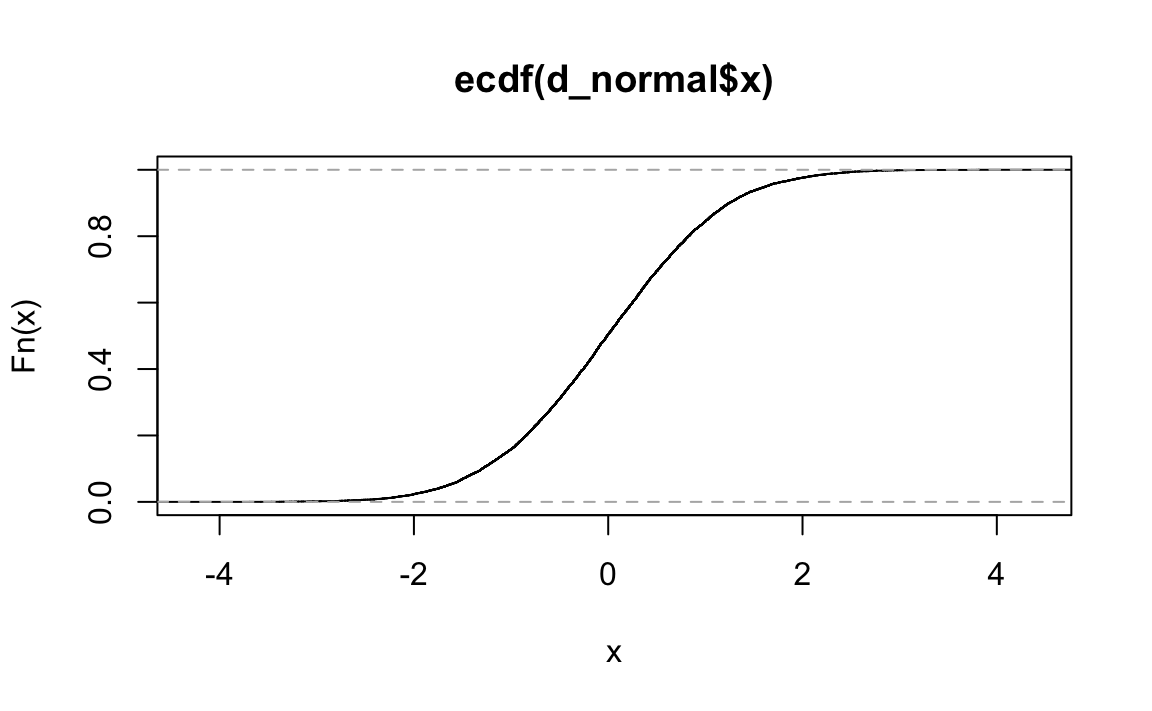
4.3 Mosaic
library(mosaic)Mit ` geht das auch schön einfach:
4.3.1 ECDF
Was ist der kumulierte Anteil für x=0:
pdata( ~ x, q = 0, data = d_normal)
#> [1] 0.50494.3.2 Quantile
Was ist das Quantil für p = .5:
qdata(~ x, p = 1/2, data = d_normal)
#> 50%
#> -0.01070173Etwa Null, passt!
5 Reproducibility
#> ─ Session info ───────────────────────────────────────────────────────────────────────────────────────────────────────
#> setting value
#> version R version 4.1.3 (2022-03-10)
#> os macOS Big Sur/Monterey 10.16
#> system x86_64, darwin17.0
#> ui X11
#> language (EN)
#> collate en_US.UTF-8
#> ctype en_US.UTF-8
#> tz Europe/Berlin
#> date 2022-05-02
#>
#> ─ Packages ───────────────────────────────────────────────────────────────────────────────────────────────────────────
#> package * version date lib source
#> assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.1.0)
#> backports 1.4.1 2021-12-13 [1] CRAN (R 4.1.0)
#> blogdown 1.8 2022-02-16 [2] CRAN (R 4.1.2)
#> bookdown 0.24.2 2021-10-15 [1] Github (rstudio/bookdown@ba51c26)
#> brio 1.1.3 2021-11-30 [1] CRAN (R 4.1.0)
#> broom 0.7.12 2022-01-28 [1] CRAN (R 4.1.2)
#> bslib 0.3.1 2021-10-06 [1] CRAN (R 4.1.0)
#> cachem 1.0.6 2021-08-19 [1] CRAN (R 4.1.0)
#> callr 3.7.0 2021-04-20 [1] CRAN (R 4.1.0)
#> cellranger 1.1.0 2016-07-27 [1] CRAN (R 4.1.0)
#> cli 3.2.0 2022-02-14 [1] CRAN (R 4.1.2)
#> codetools 0.2-18 2020-11-04 [2] CRAN (R 4.1.3)
#> colorout * 1.2-2 2022-01-04 [1] Github (jalvesaq/colorout@79931fd)
#> colorspace 2.0-3 2022-02-21 [1] CRAN (R 4.1.2)
#> crayon 1.5.1 2022-03-26 [1] CRAN (R 4.1.2)
#> DBI 1.1.2 2021-12-20 [1] CRAN (R 4.1.0)
#> dbplyr 2.1.1 2021-04-06 [1] CRAN (R 4.1.0)
#> desc 1.4.0 2021-09-28 [1] CRAN (R 4.1.0)
#> devtools 2.4.3 2021-11-30 [1] CRAN (R 4.1.0)
#> digest 0.6.29 2021-12-01 [1] CRAN (R 4.1.0)
#> dplyr * 1.0.8 2022-02-08 [1] CRAN (R 4.1.2)
#> ellipsis 0.3.2 2021-04-29 [1] CRAN (R 4.1.0)
#> evaluate 0.14 2019-05-28 [1] CRAN (R 4.1.0)
#> fansi 1.0.3 2022-03-24 [1] CRAN (R 4.1.2)
#> fastmap 1.1.0 2021-01-25 [2] CRAN (R 4.1.0)
#> forcats * 0.5.1 2021-01-27 [1] CRAN (R 4.1.0)
#> fs 1.5.2 2021-12-08 [1] CRAN (R 4.1.0)
#> generics 0.1.2 2022-01-31 [1] CRAN (R 4.1.2)
#> ggplot2 * 3.3.5 2021-06-25 [2] CRAN (R 4.1.0)
#> glue 1.6.2 2022-02-24 [1] CRAN (R 4.1.2)
#> gtable 0.3.0 2019-03-25 [1] CRAN (R 4.1.0)
#> haven 2.4.3 2021-08-04 [1] CRAN (R 4.1.0)
#> hms 1.1.1 2021-09-26 [1] CRAN (R 4.1.0)
#> htmltools 0.5.2 2021-08-25 [1] CRAN (R 4.1.0)
#> httr 1.4.2 2020-07-20 [1] CRAN (R 4.1.0)
#> jquerylib 0.1.4 2021-04-26 [1] CRAN (R 4.1.0)
#> jsonlite 1.7.3 2022-01-17 [1] CRAN (R 4.1.2)
#> knitr 1.37 2021-12-16 [1] CRAN (R 4.1.0)
#> lifecycle 1.0.1 2021-09-24 [1] CRAN (R 4.1.0)
#> lubridate 1.8.0 2021-10-07 [1] CRAN (R 4.1.0)
#> magrittr 2.0.3 2022-03-30 [1] CRAN (R 4.1.2)
#> memoise 2.0.0 2021-01-26 [2] CRAN (R 4.1.0)
#> modelr 0.1.8 2020-05-19 [1] CRAN (R 4.1.0)
#> munsell 0.5.0 2018-06-12 [1] CRAN (R 4.1.0)
#> pillar 1.7.0 2022-02-01 [1] CRAN (R 4.1.2)
#> pkgbuild 1.2.0 2020-12-15 [2] CRAN (R 4.1.0)
#> pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.1.0)
#> pkgload 1.2.4 2021-11-30 [1] CRAN (R 4.1.0)
#> prettyunits 1.1.1 2020-01-24 [1] CRAN (R 4.1.0)
#> processx 3.5.2 2021-04-30 [1] CRAN (R 4.1.0)
#> ps 1.6.0 2021-02-28 [1] CRAN (R 4.1.0)
#> purrr * 0.3.4 2020-04-17 [1] CRAN (R 4.1.0)
#> R6 2.5.1 2021-08-19 [1] CRAN (R 4.1.0)
#> Rcpp 1.0.8.3 2022-03-17 [1] CRAN (R 4.1.2)
#> readr * 2.1.2 2022-01-30 [1] CRAN (R 4.1.2)
#> readxl 1.3.1 2019-03-13 [1] CRAN (R 4.1.0)
#> remotes 2.4.0 2021-06-02 [2] CRAN (R 4.1.0)
#> reprex 2.0.1 2021-08-05 [1] CRAN (R 4.1.0)
#> rlang 1.0.2 2022-03-04 [1] CRAN (R 4.1.2)
#> rmarkdown 2.11 2021-09-14 [1] CRAN (R 4.1.0)
#> rprojroot 2.0.2 2020-11-15 [2] CRAN (R 4.1.0)
#> rstudioapi 0.13 2020-11-12 [1] CRAN (R 4.1.0)
#> rvest 1.0.2 2021-10-16 [1] CRAN (R 4.1.0)
#> sass 0.4.0 2021-05-12 [1] CRAN (R 4.1.0)
#> scales 1.2.0 2022-04-13 [1] CRAN (R 4.1.3)
#> sessioninfo 1.1.1 2018-11-05 [2] CRAN (R 4.1.0)
#> stringi 1.7.6 2021-11-29 [1] CRAN (R 4.1.0)
#> stringr * 1.4.0 2019-02-10 [1] CRAN (R 4.1.0)
#> testthat 3.1.2 2022-01-20 [1] CRAN (R 4.1.2)
#> tibble * 3.1.6 2021-11-07 [1] CRAN (R 4.1.0)
#> tidyr * 1.2.0 2022-02-01 [1] CRAN (R 4.1.2)
#> tidyselect 1.1.2 2022-02-21 [1] CRAN (R 4.1.2)
#> tidyverse * 1.3.1 2021-04-15 [1] CRAN (R 4.1.0)
#> tzdb 0.1.2 2021-07-20 [2] CRAN (R 4.1.0)
#> usethis 2.0.1 2021-02-10 [2] CRAN (R 4.1.0)
#> utf8 1.2.2 2021-07-24 [1] CRAN (R 4.1.0)
#> vctrs 0.4.0 2022-03-30 [1] CRAN (R 4.1.2)
#> withr 2.5.0 2022-03-03 [1] CRAN (R 4.1.2)
#> xfun 0.29 2021-12-14 [1] CRAN (R 4.1.0)
#> xml2 1.3.3 2021-11-30 [1] CRAN (R 4.1.0)
#> yaml 2.2.2 2022-01-25 [1] CRAN (R 4.1.2)
#>
#> [1] /Users/sebastiansaueruser/Library/R/x86_64/4.1/library
#> [2] /Library/Frameworks/R.framework/Versions/4.1/Resources/library