Welche Stufe modelliert die logististische Regression in R?

Sagen wir, wir möchten vorhersagen, ob eine Person Frau oder Mann ist (nur diese zwei Stufen) anhand der Höhe des Trinkgelds, das diese Person gibt. Dazu nutzen wir die Funktio glm() in R.

Vorbereitung

library(tidyverse)

## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.1 ──

## ✓ ggplot2 3.3.5     ✓ purrr   0.3.4
## ✓ tibble  3.1.6     ✓ dplyr   1.0.8
## ✓ tidyr   1.2.0     ✓ stringr 1.4.0
## ✓ readr   2.1.2     ✓ forcats 0.5.1

## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()

Daten

data(tips, package = "reshape2")

Die Zielvariable ist sex, sie ist nominalskaliert und sie hat zwei Stufen:

levels(tips$sex)

## [1] "Female" "Male"

Nominalskalierte Variablen werden in R als “Faktorvariablen” (factor) bezeichnet bzw. mit solchen Variablen gefasst.

1. Stufe: Female.
2. Stufe: Male.

glm() modelliert die zweite Stufe als Ereignisse von Interesse.

Das hat den Hintergrund, dass die zweite Stufe bei einer Skalierung mit den Werten 0 und 1, es ebenfalls die zweite Stufe, also die 1 ist, die von Interesse ist (normalerweise).

Die 0-1-Skalierung nennt man auch binäre Skalierung.

Was ist der mittlere Trinkgeld-Betrag zwischen den Geschlechtern?

tips %>% 
  group_by(sex) %>%
  summarise(mean(tip))

## # A tibble: 2 × 2
##   sex    `mean(tip)`
##   <fct>        <dbl>
## 1 Female        2.83
## 2 Male          3.09

Probieren wir’s aus

Hier die Zielvariable als Faktorvariable:

glm1 <- glm(sex ~ tip, data=tips, family = "binomial")
glm1

## 
## Call:  glm(formula = sex ~ tip, family = "binomial", data = tips)
## 
## Coefficients:
## (Intercept)          tip  
##      0.1703       0.1421  
## 
## Degrees of Freedom: 243 Total (i.e. Null);  242 Residual
## Null Deviance:       317.9 
## Residual Deviance: 315.9     AIC: 319.9

Hier die Zielvariable als binär skalierte Variable:

tips <-
  tips %>% 
  mutate(sex_bin = ifelse(sex == "Female", 0, 1))

Also: 0 entspricht Female. 1 entspricht Male.

glm2 <- glm(sex_bin ~ tip, data = tips, family = "binomial")
glm2

## 
## Call:  glm(formula = sex_bin ~ tip, family = "binomial", data = tips)
## 
## Coefficients:
## (Intercept)          tip  
##      0.1703       0.1421  
## 
## Degrees of Freedom: 243 Total (i.e. Null);  242 Residual
## Null Deviance:       317.9 
## Residual Deviance: 315.9     AIC: 319.9

Vergleichen wir

glm1$coefficients[["tip"]]

## [1] 0.142119

glm2$coefficients[["tip"]]

## [1] 0.142119

Identisch! Wir sehen also, die logistische Regression (allgemeiner: das generalisierte lineare Modell mit glm()) modelliert die zweite Stufe, wenn die Zielvariable eine Faktorvariable ist.

Handelt es sich um eine 0-1-skalierte Variable, so wird die “1” modelliert.

Visualisierung

pred_df <-
  tibble(
    tip = seq(min(tips$tip), max(tips$tip), by = .1),
    y = predict(glm1, type = "response", newdata = tibble(tip))
  )

ggplot(tips) +
  aes(x = tip, y = sex_bin) +
  geom_point() +
  geom_line(data = pred_df, aes(x = tip, y = y), color = "blue") +
  labs(title = "Vorhersage von `Male` in Abhängigkeit des Trinkgelds (blaue Linie)",
       subtitle = "Logististisches Modell")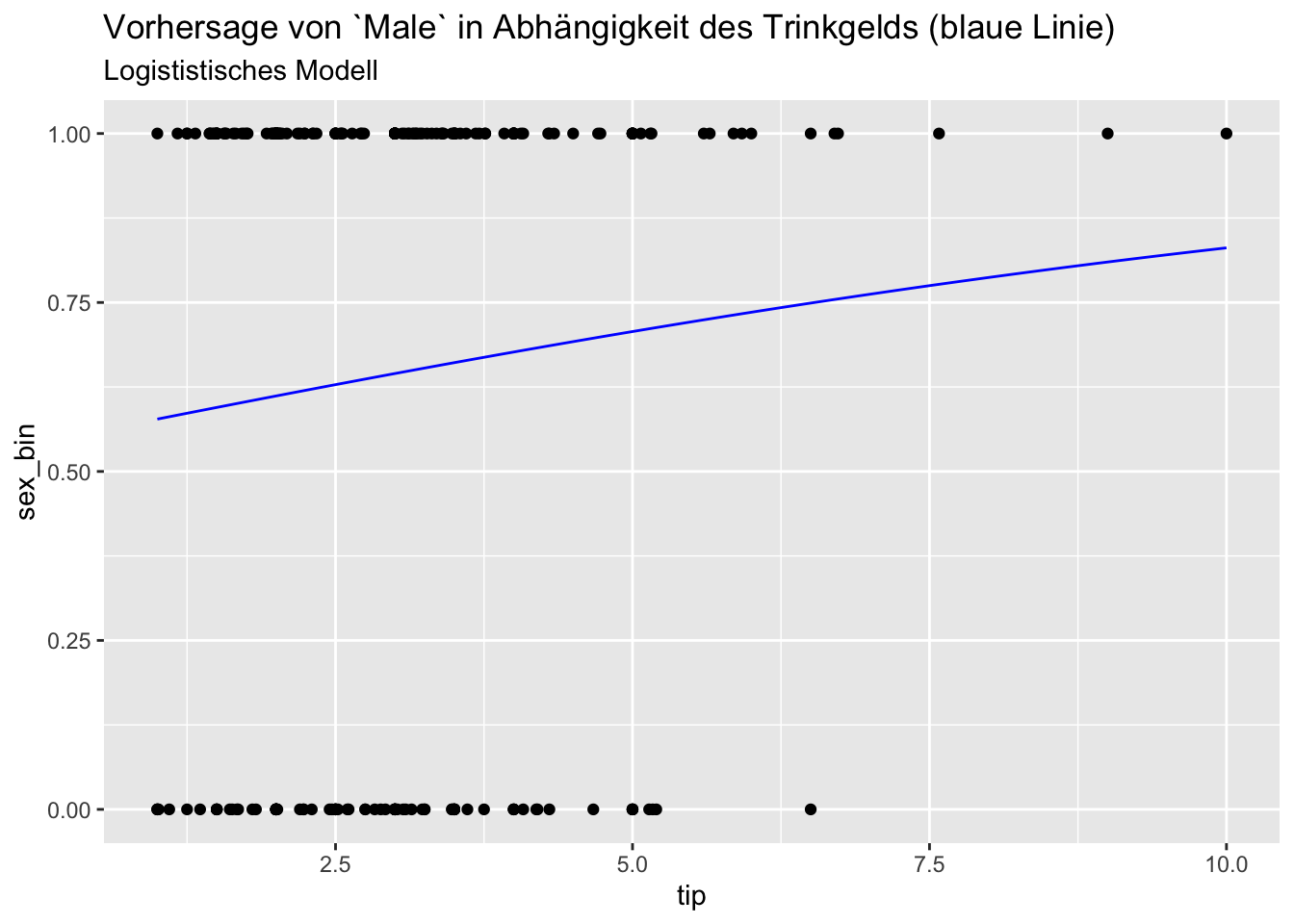

Zum Vergleich: lineare Regression

lm1 <- lm(sex_bin ~ tip, data = tips)

pred_df <-
  tibble(
    tip = seq(min(tips$tip), max(tips$tip), by = .1),
    y = predict(lm1,  newdata = tibble(tip))
  )

ggplot(tips) +
  aes(x = tip, y = sex_bin) +
  geom_point() +
  geom_line(data = pred_df, aes(x = tip, y = y), color = "blue") +
  labs(title = "Vorhersage von `Male` in Abhängigkeit des Trinkgelds (blaue Linie)",
       subtitle = "Lineares Modell")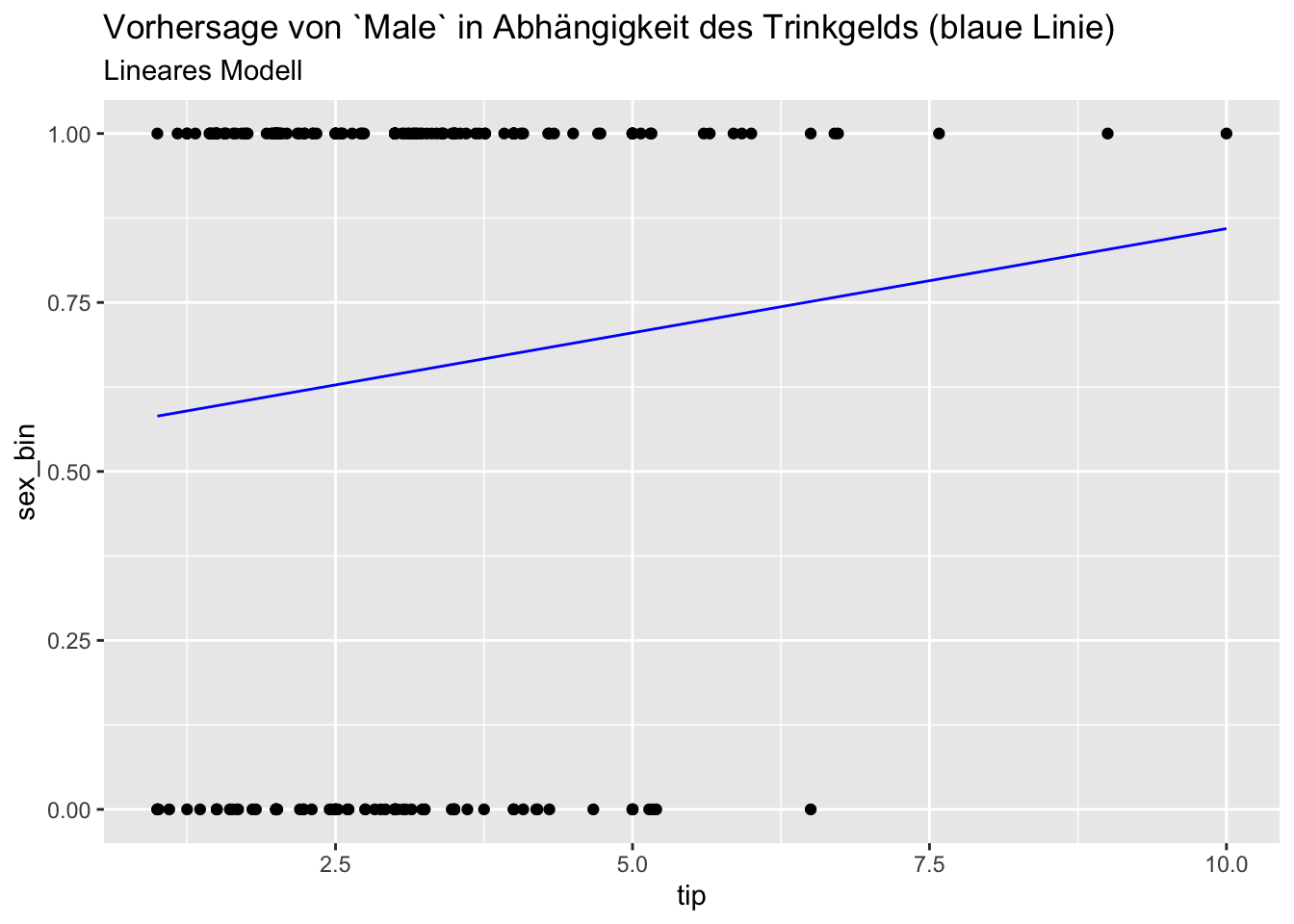

Keine großen Unterschiede (in den Vorhersagen), in diesem Fall, scheint’s.

Fazit

Für die Praxis sollte man sich merken, dass die logistische Regression in R (mit glm()) die zweite Stufe der Zielvariable modelliert.