1 R-Pakete
2 Hintergrund
Die Corona-Epidemie beherrscht (wieder) die Nachrichten, Gespräche und Gedanken. Zu Recht, aus zwei Gründen. Zum einen sind die Zahlen jetzt schon besorgniserregend, wenn nicht furchtbar. Zum anderen haben Pandemien das Potenzial zu krassen Extremwerten.
Dazu kommt, dass Falschmeldungen kursieren. Schlimmer noch als reine Unwahrheit sind Halbwahrheiten. Damit ist die Unsitte gemeint, einen einzelnen, (vielleicht) korrekten Fakt aufzugreifen, und damit eine vielschichtige Forschungsfrage für beantwortet zu erklären. Das gleicht dem Versuch, von einem 500-Teile-Puzzle ein Stück gefunden zu haben, und nun zu reklamieren, man wisse, wie das ganze Puzzle aussieht. Eher in Forschungsvokablen: Auf Basis einer Studie gibt man vor, eine Antwort auf eine breite Forschungsfrage zu geben, ohne zu erwähnen, dass es noch 50 anders geartete Studien gibt, die zu (evtl.) anderen Ergebnissen kommen.
Der Vergleich mehrerer Gruppen ist immer problematisch, problematisch in dem Maße, wie sich die Gruppen in unbekannter Weise unterscheiden. So ist es beispielsweise schwierig, die Übersterblichkeit in Deutschland in 2020 und 2021 zu vergleichen. Auf die Übersterblichkeit wirken viele Faktoren ein; so könnten etwa die Kontaktbeschränkungen dazu geführt haben, dass die Grippe sich nicht so ausbreiten konnte. Dadurch wurden Krankheits- und Todesfälle vermieden; man könnte aber auch (fälschlich) schlussfolgern, dass Corona doch “nicht so schlimm” gewesen war. Viele weitere Unterschiede sind denkbar; etwas Deltavariante vs. den Ursprungsvirus und so weiter.
Der Vergleich zwischen Ländern ist aus dem gleichen Grund noch schwieriger. Länder unterscheiden sich in vielen Hinsichten; im Hinblick auf Corona sind vermutlich klimatorische Unterschiede entscheidend. In einem warmen Land wird - bei gleicher Kontakt- oder Impfsituation - sicherlich weniger Fälle auftreten als in einem kalten Land. Das ist nur einer von vielen Unterschieden, die eine Rolle spielen können und uns zeigen, warum die Menschen Experimente erfunden haben, um die Vergleichbarkeit von Gruppen gewährleisten zu können.
Neben der Vergleichbarkeit der Daten spielt natürlich auch die Datenqualität (neben und über die Vergleichbarkeit der Datenqualität hinaus) eine wichtige Rolle. In Deutschland leistet das RKI gute Arbeit, Daten auf möglichst hohem Niveau zu sammeln. Praktischerweise sind diese Daten auch öffentlich und komfortabel zugänglich.
Im Lichte der bisher (in jüngerer Geschichte) nicht dagewesesen gesundheitlichen Gefährdungen durch die Epidemie und auch gesellschaftliche Brisanz ist die Frage nach den Fakten zu Corona und ihren Auswirkungen von höchstem Belang.
Grund genug, sich die Daten und Analysen zu Corona auf reproduzierbare Art und Weise, also transparent und für alle nachprüfbar, anzuschauen.
3 Inzidenzen in Deutschland - Daten vom RKI
Das Robert-Koch-Institut (RKI) stellt die Daten zu den Corona-Infektionen hier öffentlich zum Herunerladen bereit.
Die CSV-Datei mit den aktuellen Daten ist groß; 150 MB (26.11.21).
Die Daten werden unter der CC-BY-Lizenz bereitgestellt vom RKI.
4 Hospitalisierungen in Deutschland
Aufgrund der großen Dateigröße fangen wir mit einer kleineren Datei an. Die Datei mit den Hospitalisierungen ist viel kleiner (3MB).
Es wird auch ein adjustierter Datensatz bereitgestellt:
Zwischen dem Beginn des Krankenhausaufenthalts eines COVID-19-Falles und dem Zeitpunkt, an dem diese Information am RKI eingeht, entsteht ein zeitlicher Verzug. Um den Trend der Anzahl von Hospitalisierungen und der 7-Tage-Hospitalisierungsinzidenz besser bewerten zu können, ergänzen wir die berichtete Hospitalisierungsinzidenz um eine Schätzung der zu erwartenden Anzahl an verzögert berichteten Hospitalisierungen. Neben den Daten der gemeldeten COVID-19-Hospitalisierungen auf Bundes- und Länderebene wird daher ein Nowcasting der Anzahl hospitalisierter Fälle und der 7-Tage-Hospitalisierungsinzidenz auf Bundesebene durchgeführt. Ziel ist die Schätzung der Anzahl von hospitalisierten COVID-19-Fällen mit Meldedatum innerhalb der sieben vorhergehenden Tage - inklusive der noch nicht an das RKI berichteten Hospitalisierungen.
Schauen wir uns den neuesten (adjustierten) Datensatz näher an.
Zur Berechnung der adjustierten 7T-Inzidenz schreibt das RKI hier:
Die adjustierte 7-Tage-Hospitalisierungsinzidenz berechnet sich aus der adjustierten Anzahl der hospitalisierten COVID-19-Fälle der letzten sieben Tage (vorherig des Berichtsdatums) und der Bevölkerungszahl. Zur einheitlichen Darstellung wird die Inzidenz auf 100.000 Bevölkerung normiert.
4.1 Adjustierte Daten
4.1.1 Daten importieren
Weitere Informationen - wie das Codebook (d.h. die Erläuterungen zu den Variablen) - finden Sie auf dem Github-Repo des RKI.
hosp_file <- "https://raw.githubusercontent.com/robert-koch-institut/COVID-19-Hospitalisierungen_in_Deutschland/master/Archiv/2021-11-24_Deutschland_adjustierte-COVID-19-Hospitalisierungen.csv"
hosp_adj <- read_csv(hosp_file) # adj wie "adjustiert"4.1.2 EDA
hosp_adj %>%
ggplot() +
aes(x = Datum, y = PS_adjustierte_7T_Hospitalisierung_Inzidenz) +
geom_line() 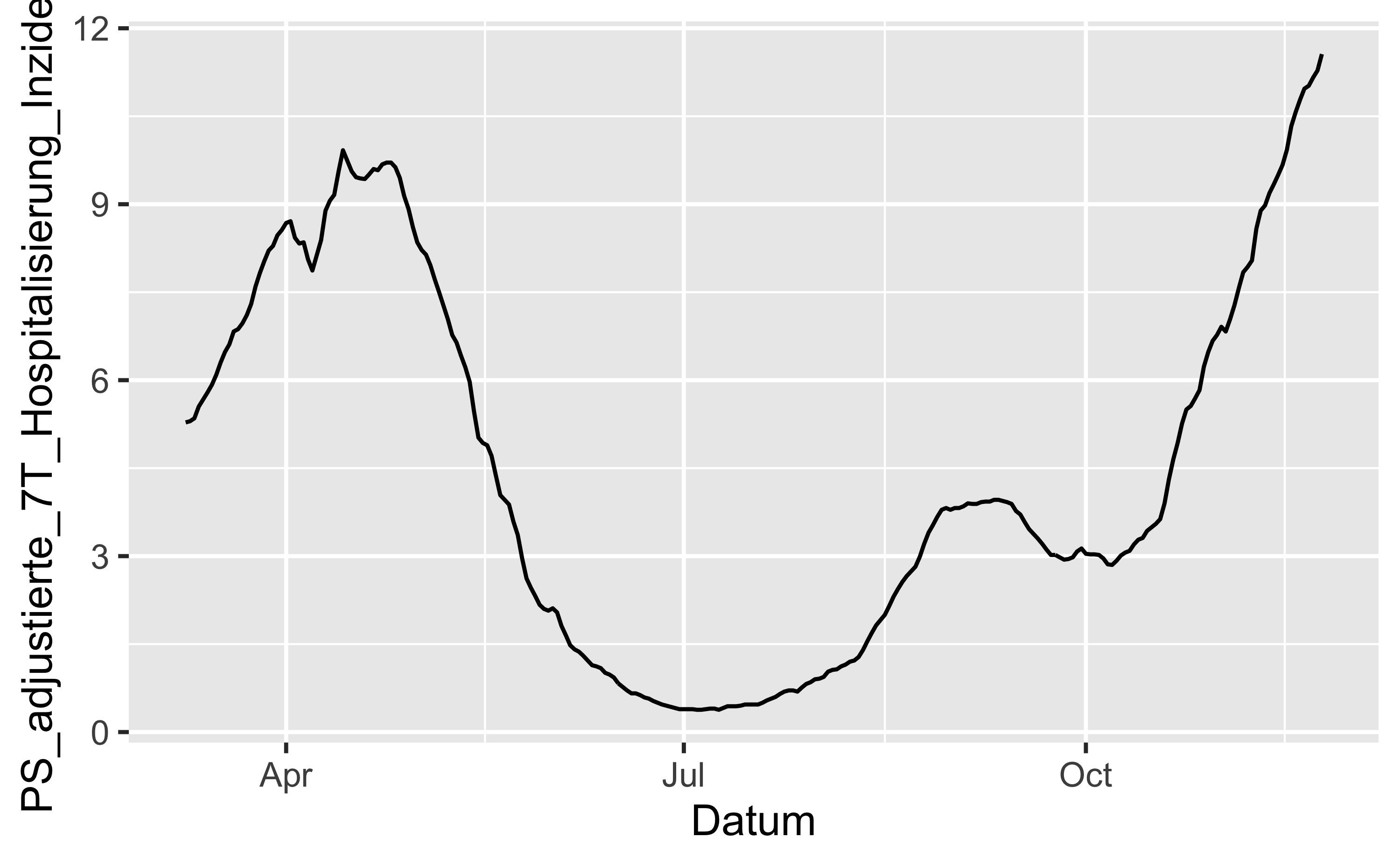
4.2 Unadjustierte Daten
4.2.1 Daten importieren
hosp_latest_file <- "https://github.com/robert-koch-institut/COVID-19-Hospitalisierungen_in_Deutschland/raw/master/Archiv/2021-11-27_Deutschland_COVID-19-Hospitalisierungen.csv"
hosp_latest <- read_csv(hosp_latest_file)4.2.2 EDA
4.2.2.1 Bundesgebiet
hosp_latest %>%
filter(Bundesland == "Bundesgebiet") %>%
ggplot() +
aes(x = Datum, y = `7T_Hospitalisierung_Inzidenz`) +
geom_line(aes(color = Altersgruppe)) +
scale_color_brewer(type = "qual")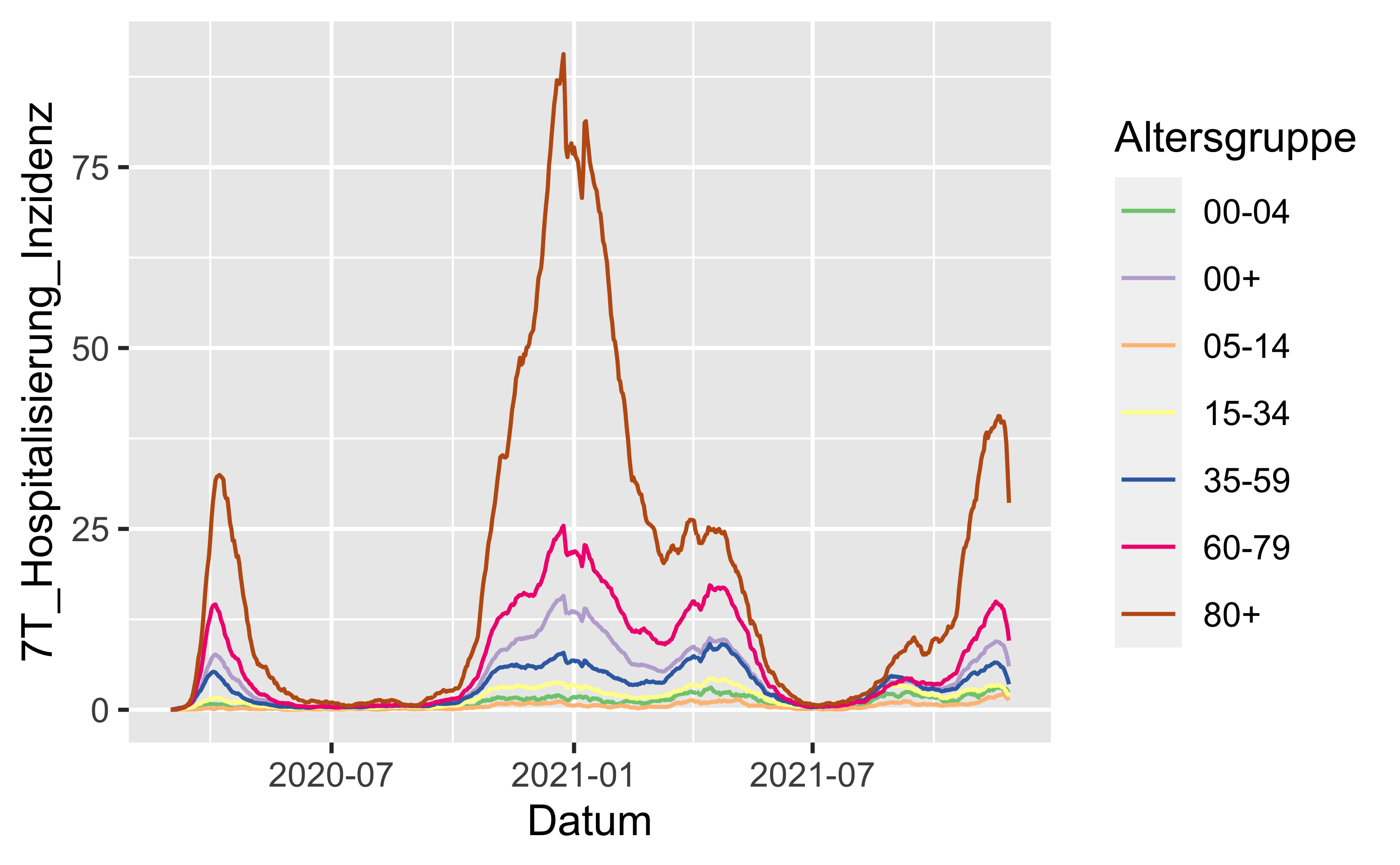
4.2.2.2 Nach Bundesland
hosp_latest %>%
filter(Bundesland != "Bundesgebiet") %>%
ggplot() +
aes(x = Datum, y = `7T_Hospitalisierung_Inzidenz`) +
geom_line(aes(color = Altersgruppe)) +
scale_color_brewer(type = "qual") +
facet_wrap(~ Bundesland)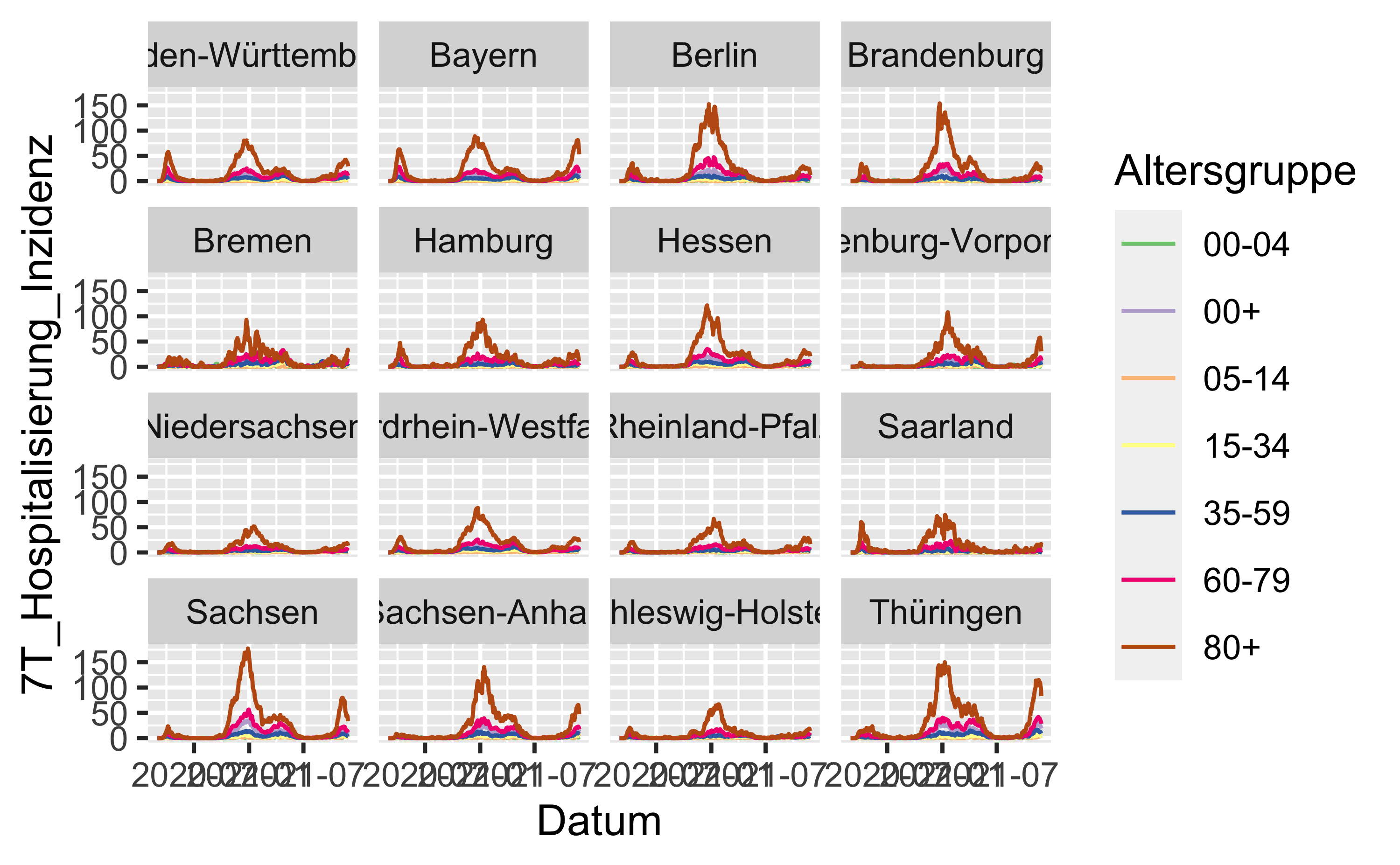
hosp_latest %>%
filter(Bundesland != "Bundesgebiet") %>%
filter(Datum == max(Datum)) %>%
select(-Bundesland_Id, -`7T_Hospitalisierung_Faelle`) %>%
mutate(Bundesland = factor(Bundesland)) %>%
group_by(Bundesland) %>%
summarise(Inz_7T_Hosp = mean(`7T_Hospitalisierung_Inzidenz`)) %>%
ggplot() +
aes(y = fct_reorder(Bundesland, Inz_7T_Hosp), x = Inz_7T_Hosp) +
geom_col()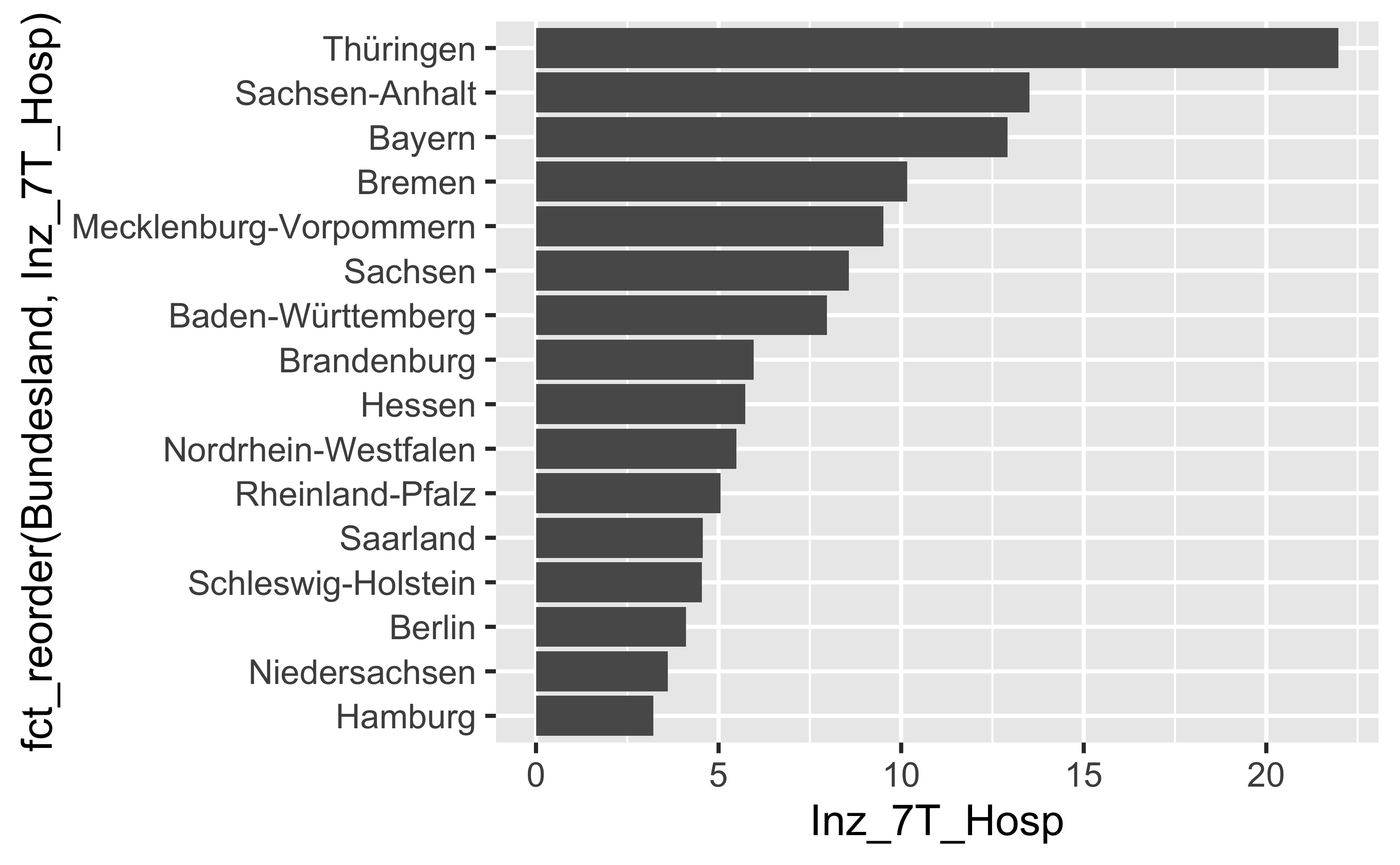
4.2.2.3 Nach Datum
Erstellen wir ein paar weitere Variablen, die das Datum widerspiegeln:
hosp_latest <-
hosp_latest %>%
mutate(Monat = month(Datum),
Woche = week(Datum),
Quartal = quarter(Datum),
Jahr = year(Datum)) %>%
select(Datum, Monat, Woche, Quartal, Jahr, everything())5 Impfungen in Deutschland
Weitere Informationen - wie das Codebook (d.h. die Erläuterungen zu den Variablen) - finden Sie auf dem Github-Repo des RKI.
5.1 Neueste Daten
5.1.1 Daten laden
Von diesem Github-Repo kann man sich die Impfdaten beim RKI herunterladen.
Die Daten werden sogar pro Landkreis bereitgestellt. Wir begnügen uns hier aber mit den Daten pro Bundesland.
vacc_file_latest <- "https://raw.githubusercontent.com/robert-koch-institut/COVID-19-Impfungen_in_Deutschland/master/Archiv/2021-11-27_Deutschland_Impfquoten_COVID-19.csv"
vacc_latest <- read_csv(vacc_file_latest)glimpse(vacc_latest)## Rows: 18
## Columns: 22
## $ Datum <date> 2021-11-26, 2021-11-26, 2021-11-26, 2021-11-2…
## $ Bundesland <chr> "Deutschland", "Schleswig-Holstein", "Hamburg"…
## $ BundeslandId_Impfort <chr> "00", "01", "02", "03", "04", "05", "06", "07"…
## $ Impfungen_gesamt <dbl> 121165530, 4496736, 2866180, 11883793, 1147170…
## $ Impfungen_gesamt_min1 <dbl> 59121827, 2189818, 1412757, 5868583, 563007, 1…
## $ Impfungen_gesamt_voll <dbl> 56862343, 2115139, 1373514, 5621902, 544534, 1…
## $ Impfungen_gesamt_boost <dbl> 8611480, 323441, 176822, 812783, 84998, 200130…
## $ Impfquote_gesamt_min1 <dbl> 71.1, 75.2, 76.3, 73.3, 82.8, 75.1, 71.0, 72.3…
## $ Impfquote_12bis17_min1 <dbl> 51.9, 65.3, 53.2, 59.1, 55.2, 58.8, 52.0, 53.8…
## $ Impfquote_18plus_min1 <dbl> 81.8, 87.2, 88.5, 84.0, 95.6, 86.3, 81.8, 82.9…
## $ Impfquote_18bis59_min1 <dbl> 74.3, 81.0, 83.5, 74.5, 92.2, 78.7, 75.1, 74.2…
## $ Impfquote_60plus_min1 <dbl> 87.2, 90.2, 88.7, 90.3, 94.8, 90.7, 87.3, 89.9…
## $ Impfquote_gesamt_voll <dbl> 68.4, 72.7, 74.1, 70.2, 80.1, 71.7, 67.5, 68.1…
## $ Impfquote_12bis17_voll <dbl> 45.9, 58.6, 48.8, 52.6, 50.9, 53.2, 45.6, 46.6…
## $ Impfquote_18plus_voll <dbl> 79.0, 84.6, 86.2, 80.8, 92.7, 82.6, 78.1, 78.4…
## $ Impfquote_18bis59_voll <dbl> 75.3, 81.5, 85.8, 76.6, 92.3, 79.4, 74.8, 73.9…
## $ Impfquote_60plus_voll <dbl> 86.0, 90.0, 87.4, 88.5, 93.3, 88.8, 84.7, 86.5…
## $ Impfquote_gesamt_boost <dbl> 10.4, 11.1, 9.5, 10.2, 12.5, 11.2, 9.1, 10.0, …
## $ Impfquote_12bis17_boost <dbl> 1.0, 0.4, 1.2, 1.1, 0.5, 1.1, 1.0, 1.2, 0.9, 1…
## $ Impfquote_18plus_boost <dbl> 12.3, 13.3, 11.4, 12.1, 14.9, 13.4, 10.9, 11.8…
## $ Impfquote_18bis59_boost <dbl> 6.9, 6.5, 6.9, 6.8, 7.6, 7.6, 6.0, 6.3, 5.9, 8…
## $ Impfquote_60plus_boost <dbl> 22.6, 25.2, 22.8, 22.0, 29.8, 24.4, 20.6, 21.9…Die Datei gibt die Impfquote für einen Tag (hier 27.11.21) wieder.
5.1.2 EDA
vacc_latest %>%
#filter(Bundesland != "Deutschland") %>%
mutate(Bundesland = factor(Bundesland)) %>%
ggplot() +
aes(y = fct_reorder(Bundesland, Impfquote_gesamt_voll),
x = Impfquote_gesamt_voll) +
geom_col() +
labs(title = "Impfquote am 27.11.2021",
caption = "Datenquelle: RKI")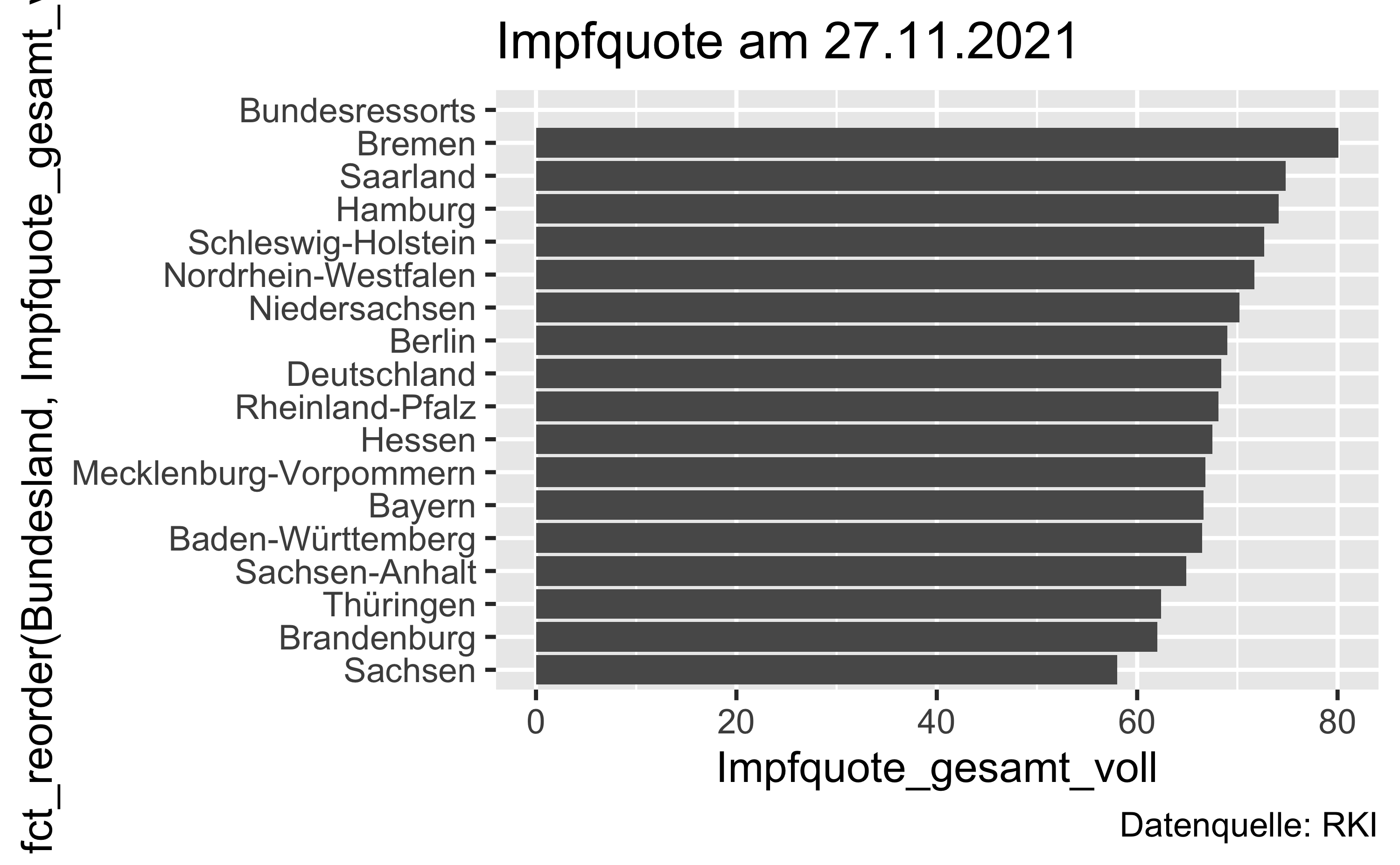
Und hier als Vektor der Impfquoten (genauer gesagt: Impfquote_gesamt_voll), absteigend sortiert:
vacc_latest_df <-
vacc_latest %>%
filter(!Bundesland %in% c("Bundesressorts", "Deutschland")) %>%
mutate(Bundesland = factor(Bundesland)) %>%
select(Bundesland, Impfquote_gesamt_voll) %>%
arrange(-Impfquote_gesamt_voll)
vacc_latest_df %>%
gt() %>%
tab_options(
heading.align = "left"
)| Bundesland | Impfquote_gesamt_voll |
|---|---|
| Bremen | 80.1 |
| Saarland | 74.8 |
| Hamburg | 74.1 |
| Schleswig-Holstein | 72.7 |
| Nordrhein-Westfalen | 71.7 |
| Niedersachsen | 70.2 |
| Berlin | 69.0 |
| Rheinland-Pfalz | 68.1 |
| Hessen | 67.5 |
| Mecklenburg-Vorpommern | 66.8 |
| Bayern | 66.6 |
| Baden-Württemberg | 66.5 |
| Sachsen-Anhalt | 64.9 |
| Thüringen | 62.4 |
| Brandenburg | 62.0 |
| Sachsen | 58.0 |
Und wir speichern die Reihenfolge der Bundesländer nach Impfquote für spätere Verwendung in einem Vektor:
bundeslaender_nach_impfquote <-
vacc_latest_df %>%
pull(Bundesland) %>%
fct_inorder() # Faktorstufen ordnen entsprechend ihrer empirischen Reihenfolge
bundeslaender_nach_impfquote## [1] Bremen Saarland Hamburg
## [4] Schleswig-Holstein Nordrhein-Westfalen Niedersachsen
## [7] Berlin Rheinland-Pfalz Hessen
## [10] Mecklenburg-Vorpommern Bayern Baden-Württemberg
## [13] Sachsen-Anhalt Thüringen Brandenburg
## [16] Sachsen
## 16 Levels: Bremen Saarland Hamburg Schleswig-Holstein ... Sachsen5.2 Impfquoten im Zeitverlauf
5.2.1 Daten laden 1
vacc_time_file <- "https://raw.githubusercontent.com/robert-koch-institut/COVID-19-Impfungen_in_Deutschland/master/Archiv/2021-11-24_Deutschland_Bundeslaender_COVID-19-Impfungen.csv"
vacc_time <- read_csv(vacc_time_file)glimpse(vacc_time)## Rows: 33,773
## Columns: 5
## $ Impfdatum <date> 2020-12-27, 2020-12-27, 2020-12-27, 2020-12-27, …
## $ BundeslandId_Impfort <chr> "01", "02", "03", "04", "04", "05", "05", "06", "…
## $ Impfstoff <chr> "Comirnaty", "Comirnaty", "Comirnaty", "Comirnaty…
## $ Impfserie <dbl> 1, 1, 1, 1, 1, 1, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1…
## $ Anzahl <dbl> 808, 443, 373, 511, 3, 8721, 9, 2712, 2, 1252, 26…Diese Datei gibt uns nicht direkt die Impfquoten, sondern die Anzahl der Impfungen pro Bundesland pro Tag. Einfacher ist es vielleicht, die Dateien zu suchen, die uns die Impfquoten schon komfortabel zur Verfügung stellen.
5.2.2 Daten laden 2
5.2.2.1 Relevante Daten finden
Im RKI-Repo finden sich dazu Dateien mit dem Namen JJJJ-MM-TT_Deutschland_Impfquoten_COVID-19.csv.
Unser Plan muss wohl sein, alle diese Dateien zusammenzutragen und dann in eine Tabelle (Dataframe) zusammenzufügen.
Da ich das Repo auf meine Festplatte heruntergeladen habe, kann ich recht komfortabel eine Liste der relevanten Dateien bekommen:
vacc_dir <- "/Users/sebastiansaueruser/github-repos/COVID-19-Impfungen_in_Deutschland/Archiv"
search_term <- "^\\d{4}-\\d{2}-\\d{2}_Deutschland_Impfquoten_COVID-19.csv$"
vacc_time_files <-
list.files(path = vacc_dir,
pattern = search_term)head(vacc_time_files)## [1] "2021-09-17_Deutschland_Impfquoten_COVID-19.csv"
## [2] "2021-09-18_Deutschland_Impfquoten_COVID-19.csv"
## [3] "2021-09-20_Deutschland_Impfquoten_COVID-19.csv"
## [4] "2021-09-21_Deutschland_Impfquoten_COVID-19.csv"
## [5] "2021-09-22_Deutschland_Impfquoten_COVID-19.csv"
## [6] "2021-09-23_Deutschland_Impfquoten_COVID-19.csv"length(vacc_time_files)## [1] 58Wir haben also Daten von 58 Daten.
5.2.2.2 Daten importieren
Zwar liegen die Daten auch auf meinem Rechner, aber für die geneigten Lesis ist es vermutlich einfacher, die Daten direkt vom RKI-Repo zu importieren.
Dafür müssen wir zuerst für jede Datei den Pfad vorne anfügen:
vacc_path <- "https://raw.githubusercontent.com/robert-koch-institut/COVID-19-Impfungen_in_Deutschland/master/Archiv"
vacc_time_files_w_path <-
paste0(vacc_path, "/", vacc_time_files)head(vacc_time_files_w_path)## [1] "https://raw.githubusercontent.com/robert-koch-institut/COVID-19-Impfungen_in_Deutschland/master/Archiv/2021-09-17_Deutschland_Impfquoten_COVID-19.csv"
## [2] "https://raw.githubusercontent.com/robert-koch-institut/COVID-19-Impfungen_in_Deutschland/master/Archiv/2021-09-18_Deutschland_Impfquoten_COVID-19.csv"
## [3] "https://raw.githubusercontent.com/robert-koch-institut/COVID-19-Impfungen_in_Deutschland/master/Archiv/2021-09-20_Deutschland_Impfquoten_COVID-19.csv"
## [4] "https://raw.githubusercontent.com/robert-koch-institut/COVID-19-Impfungen_in_Deutschland/master/Archiv/2021-09-21_Deutschland_Impfquoten_COVID-19.csv"
## [5] "https://raw.githubusercontent.com/robert-koch-institut/COVID-19-Impfungen_in_Deutschland/master/Archiv/2021-09-22_Deutschland_Impfquoten_COVID-19.csv"
## [6] "https://raw.githubusercontent.com/robert-koch-institut/COVID-19-Impfungen_in_Deutschland/master/Archiv/2021-09-23_Deutschland_Impfquoten_COVID-19.csv"Könnte klappen…
Jetzt “mappen” wir auf jeden Dateinamen die Funktion read_csv:
tic()
vacc_time_df <-
vacc_time_files_w_path %>%
map_df(read_csv)
toc()## 7.404 sec elapsedDa das etwas Zeit kostet, macht es vielleicht Sinn, den Datensatz lokal abzuspeichern.
write_csv(vacc_time_df,
file = "/Users/sebastiansaueruser/datasets/Covid/vacc_time_df.csv")Halt, besser noch in diesem Repo, damit die Daten für Sie einfach zugreifbar sind:
write_csv(vacc_time_df,
file = "static/datasets/vacc_time_df.csv")Nämlich so:
vacc_time_df <-
read_csv("https://raw.githubusercontent.com/sebastiansauer/sesa-blog/main/static/datasets/vacc_time_df.csv")Sie können hier die Daten herunterladen.
5.3 EDA
5.3.1 Impfquote Deutschland im Zeitverlauf
vacc_time_df %>%
filter(Bundesland == "Deutschland") %>%
ggplot() +
aes(x = Datum, y = Impfquote_gesamt_voll) +
geom_line()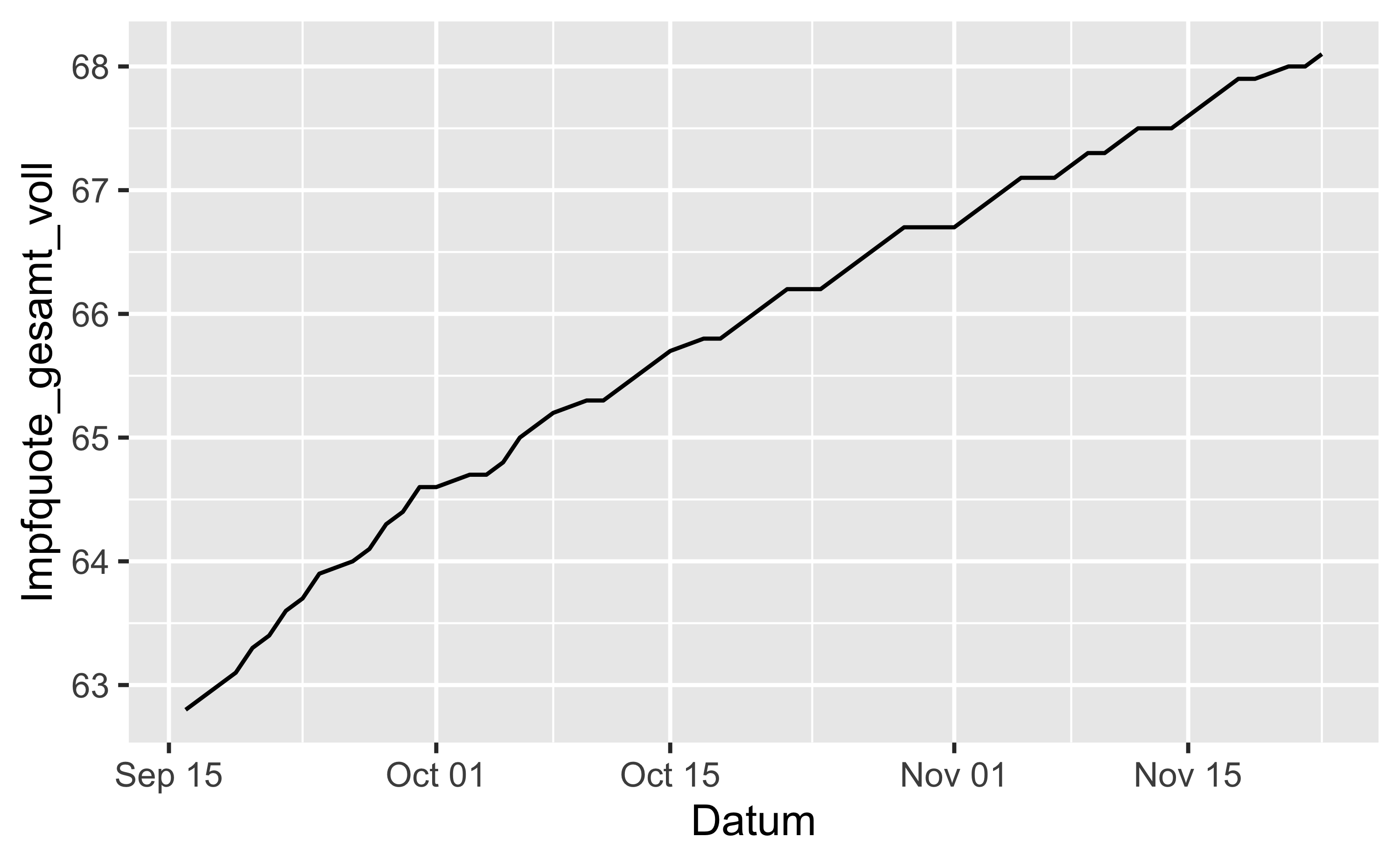
5.3.2 Impfquote der Bundesländer im Zeitverlauf
vacc_time_df %>%
filter(!Bundesland %in% c("Deutschland", "Bundesressorts")) %>%
ggplot() +
aes(x = Datum, y = Impfquote_gesamt_voll) +
geom_line() +
facet_wrap(~ Bundesland, ncol = 4)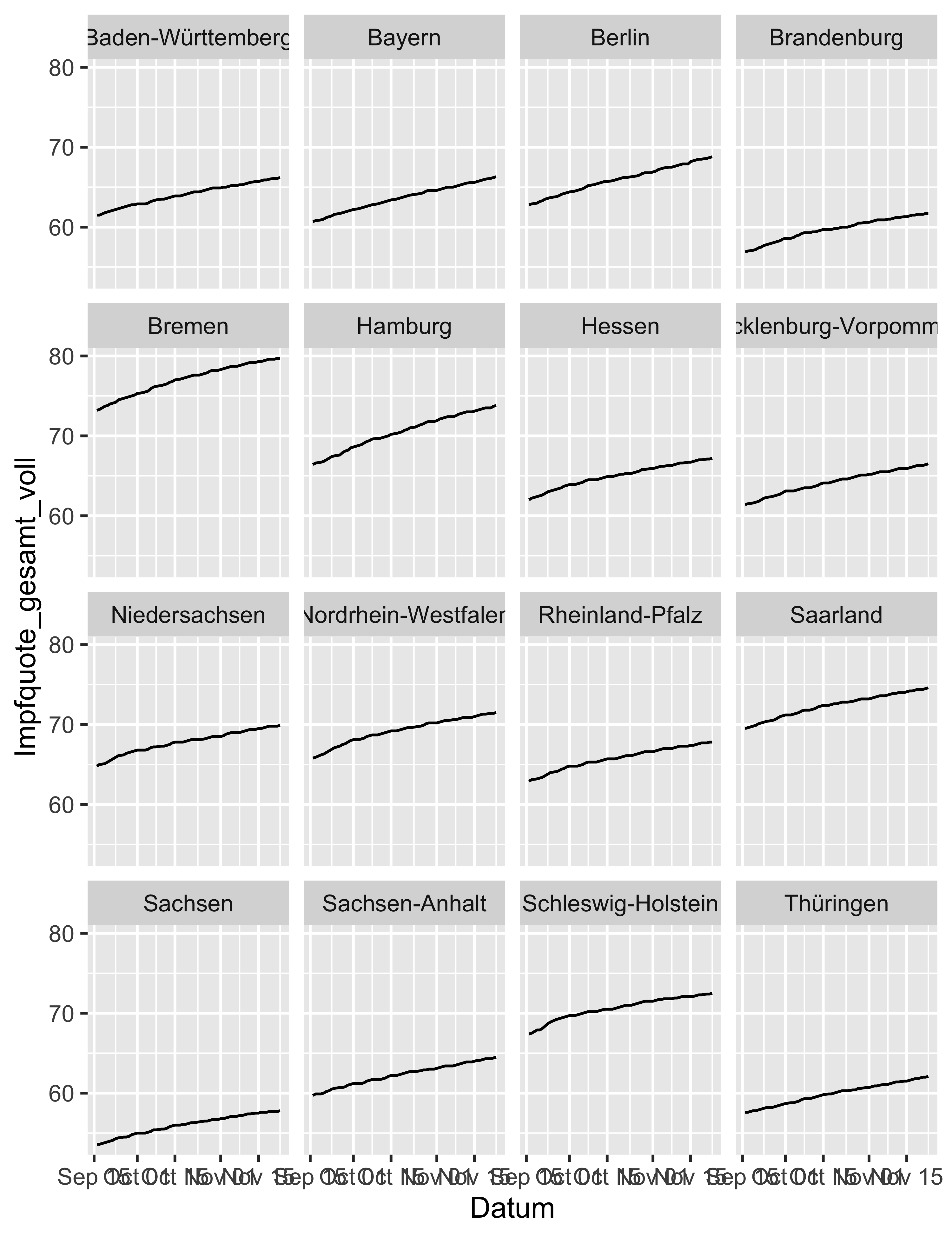
vacc_time_df %>%
filter(Bundesland != "Deutschland") %>%
ggplot() +
aes(x = Datum, y = Impfquote_gesamt_voll, color = Bundesland) +
geom_line() +
scale_color_viridis_d()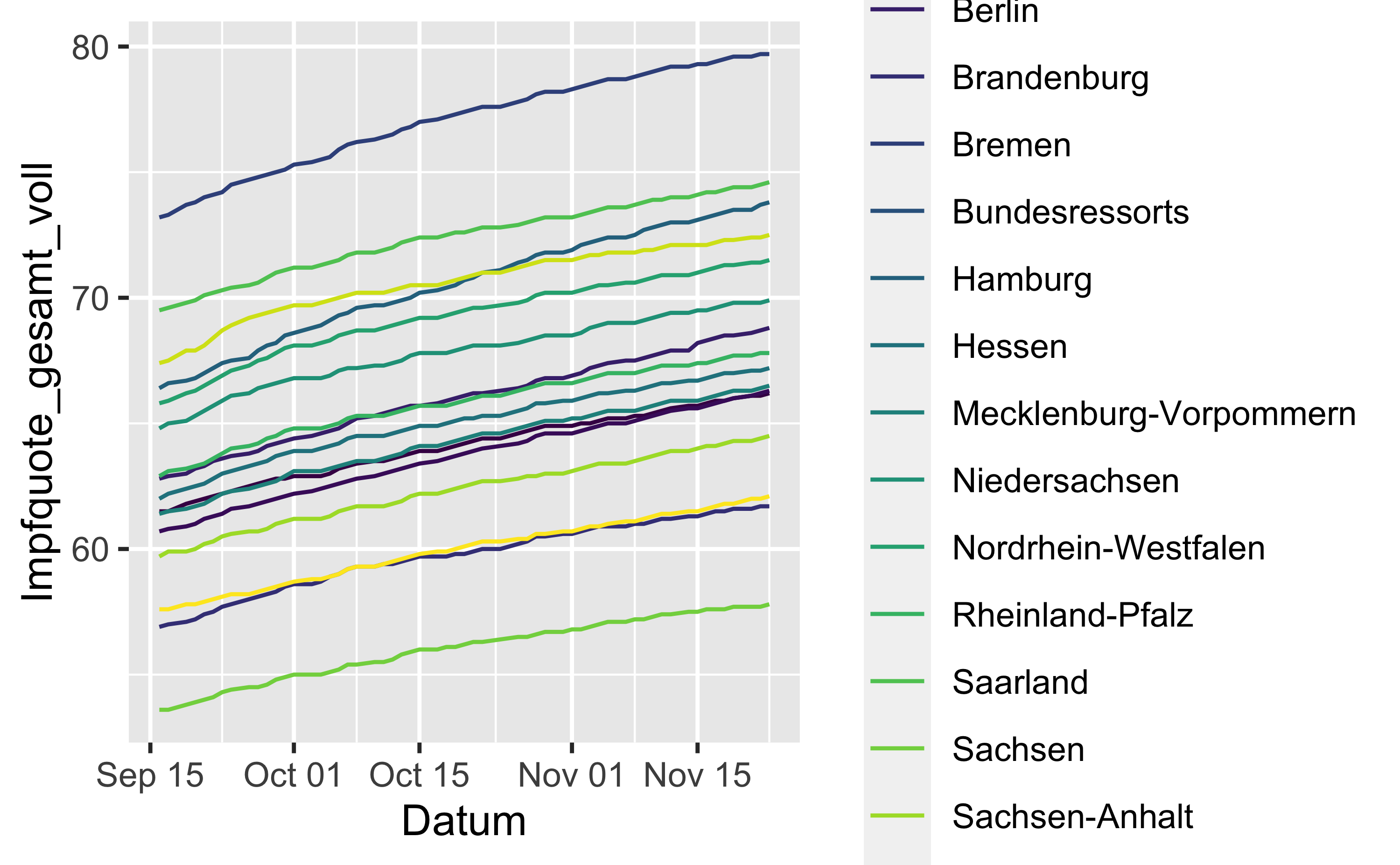
Die Daten reichen von … bis … :
vacc_time_df %>%
filter(Datum == min(Datum)) %>%
pull(Datum)## [1] "2021-09-16" "2021-09-16" "2021-09-16" "2021-09-16" "2021-09-16"
## [6] "2021-09-16" "2021-09-16" "2021-09-16" "2021-09-16" "2021-09-16"
## [11] "2021-09-16" "2021-09-16" "2021-09-16" "2021-09-16" "2021-09-16"
## [16] "2021-09-16" "2021-09-16" "2021-09-16"vacc_time_df %>%
filter(Datum == max(Datum)) %>%
pull(Datum)## [1] "2021-11-23" "2021-11-23" "2021-11-23" "2021-11-23" "2021-11-23"
## [6] "2021-11-23" "2021-11-23" "2021-11-23" "2021-11-23" "2021-11-23"
## [11] "2021-11-23" "2021-11-23" "2021-11-23" "2021-11-23" "2021-11-23"
## [16] "2021-11-23" "2021-11-23" "2021-11-23"Noch ein ganz nettes Detail: Sortieren wir die Legende nach der Höhe der Impfquote.
Zuerst brauchen wir eine nach Impfquote geordnete Liste. Die haben wir oben schon mal erstellt:
bundeslaender_nach_impfquote## [1] Bremen Saarland Hamburg
## [4] Schleswig-Holstein Nordrhein-Westfalen Niedersachsen
## [7] Berlin Rheinland-Pfalz Hessen
## [10] Mecklenburg-Vorpommern Bayern Baden-Württemberg
## [13] Sachsen-Anhalt Thüringen Brandenburg
## [16] Sachsen
## 16 Levels: Bremen Saarland Hamburg Schleswig-Holstein ... Sachsenvacc_time_df %>%
filter(Bundesland != "Deutschland") %>%
ggplot() +
aes(x = Datum, y = Impfquote_gesamt_voll, color = Bundesland) +
geom_line() +
scale_color_viridis_d(breaks = bundeslaender_nach_impfquote)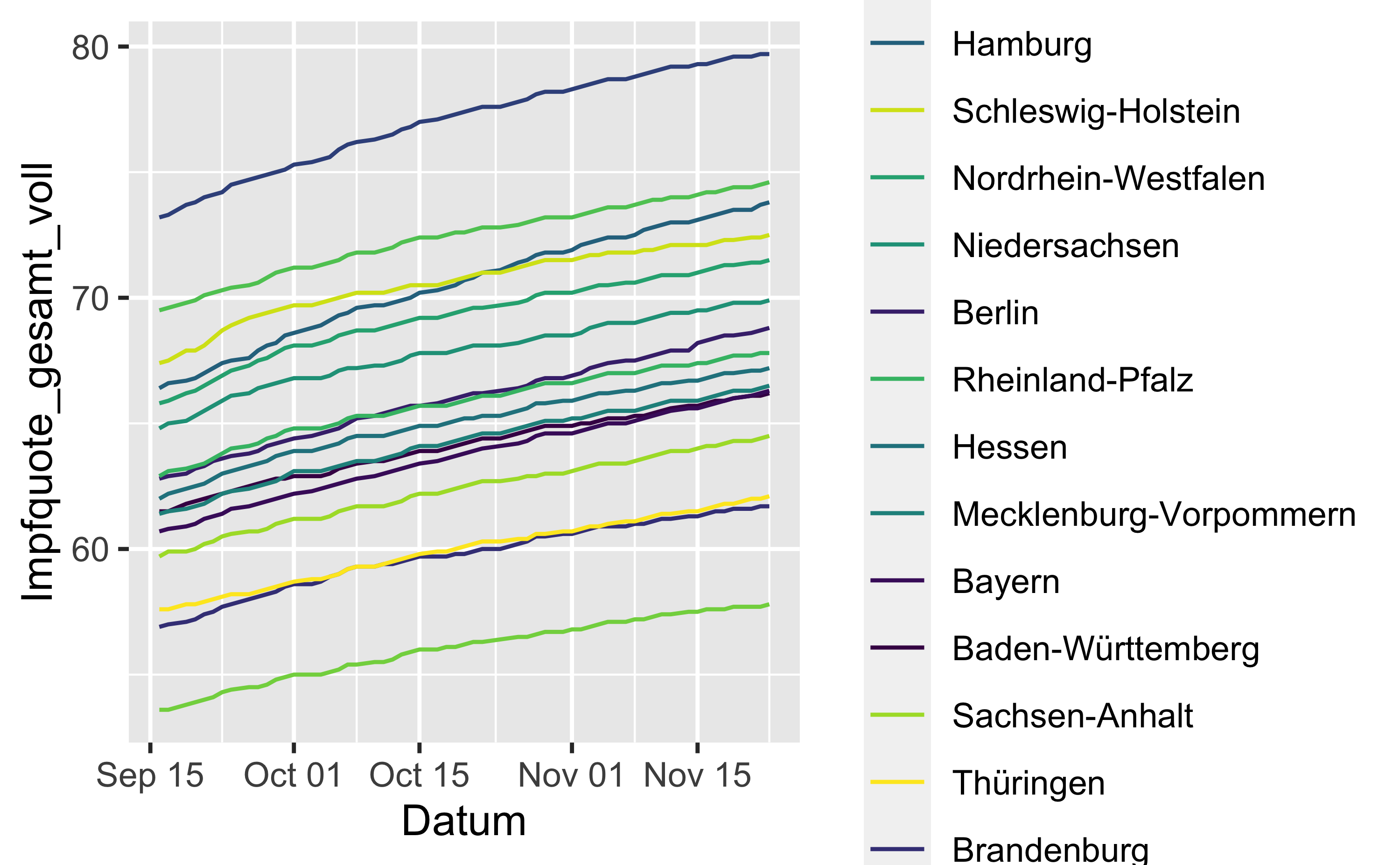
Häufig ist es sinnvoll, Liniendiagramme mit mehreren Linien gleich mit dem passenden Label zu versehen. Probieren wir das:
vacc_time_df %>%
filter(Bundesland != "Deutschland") %>%
ggplot() +
aes(x = Datum, y = Impfquote_gesamt_voll, color = Bundesland) +
geom_line() +
scale_color_viridis_d(breaks = NULL) +
geom_label(data = vacc_time_df %>% filter(Datum == max(Datum)),
aes(label = Bundesland),
size = 2)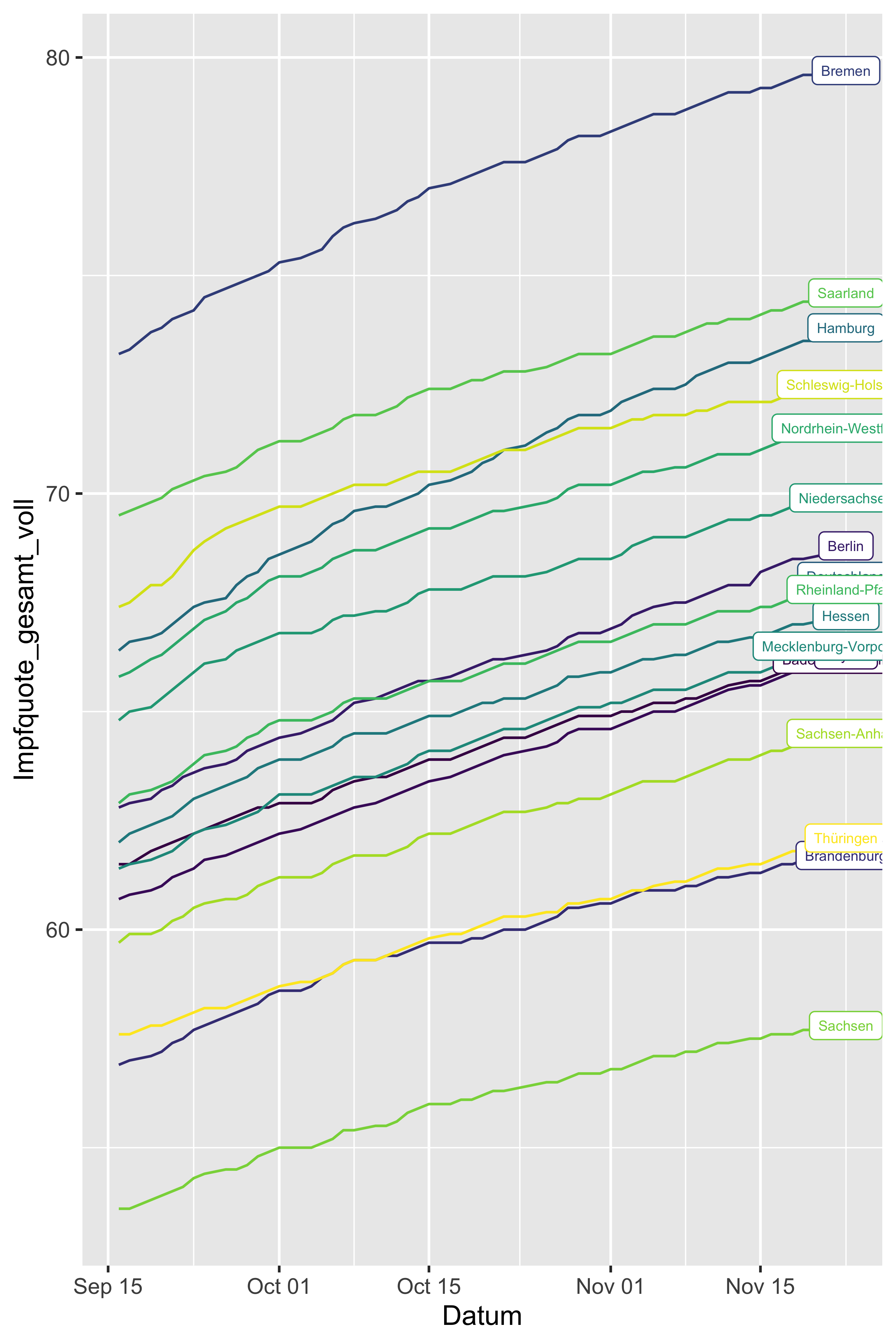
Hm. Die Position der Labels ist nicht gut. Vielleicht etwas dezenter?
vacc_time_df %>%
filter(Bundesland != "Deutschland") %>%
ggplot() +
aes(x = Datum, y = Impfquote_gesamt_voll, color = Bundesland) +
geom_line() +
scale_color_viridis_d(breaks = NULL) +
geom_text(data = vacc_time_df %>% filter(Datum == max(Datum),
Bundesland != "Deutschland"),
aes(label = Bundesland),
size = 2,
nudge_x = +5)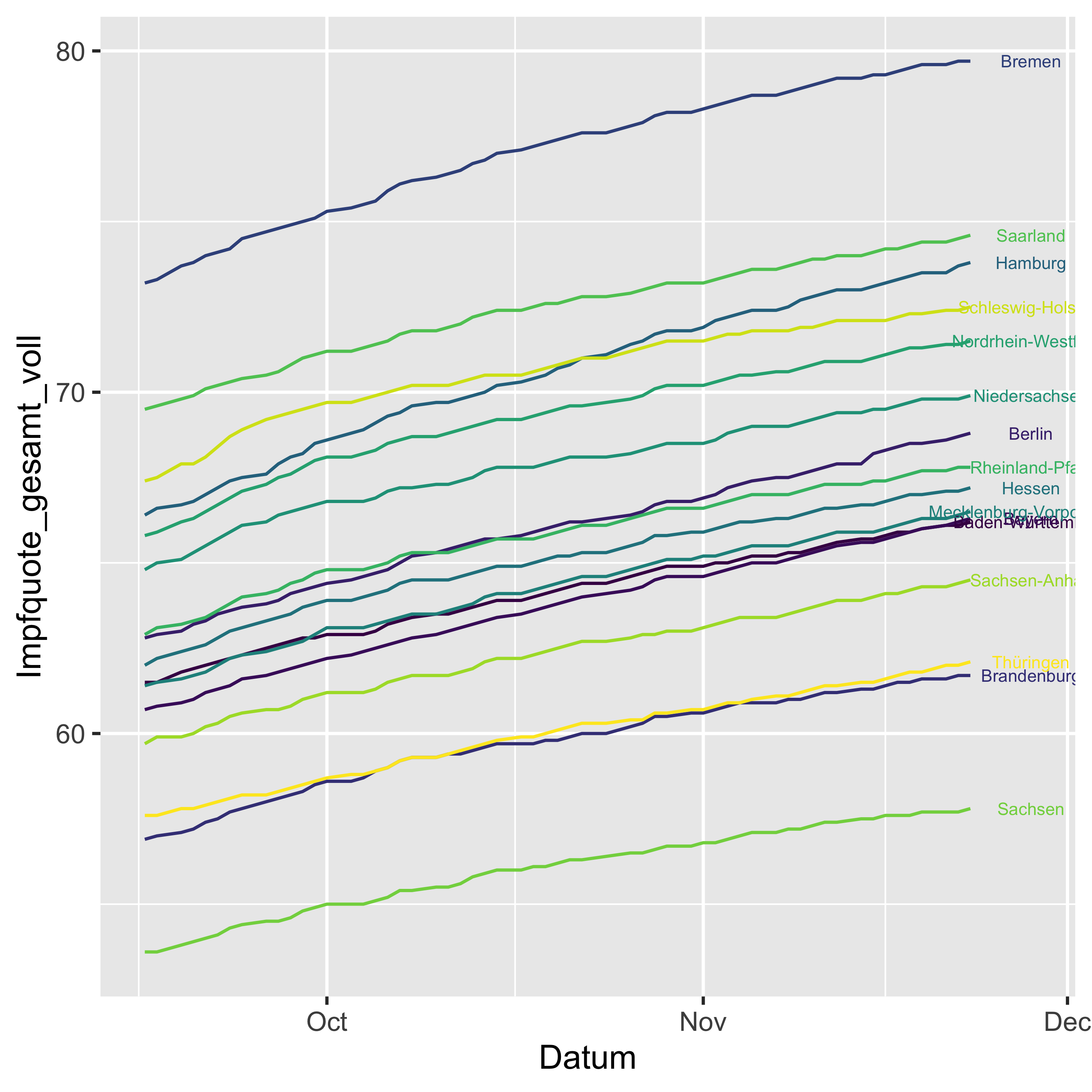
Naja, ok.
Oder vielleicht mit geom_label_repel(), das versucht, Überschneidungen der Labels zu verhindern:
vacc_time_df %>%
filter(Bundesland != "Deutschland") %>%
ggplot() +
aes(x = Datum, y = Impfquote_gesamt_voll, color = Bundesland) +
geom_line() +
scale_color_viridis_d(breaks = NULL) +
geom_label_repel(data = vacc_time_df %>% filter(Datum == max(Datum),
Bundesland != "Deutschland"),
aes(label = Bundesland))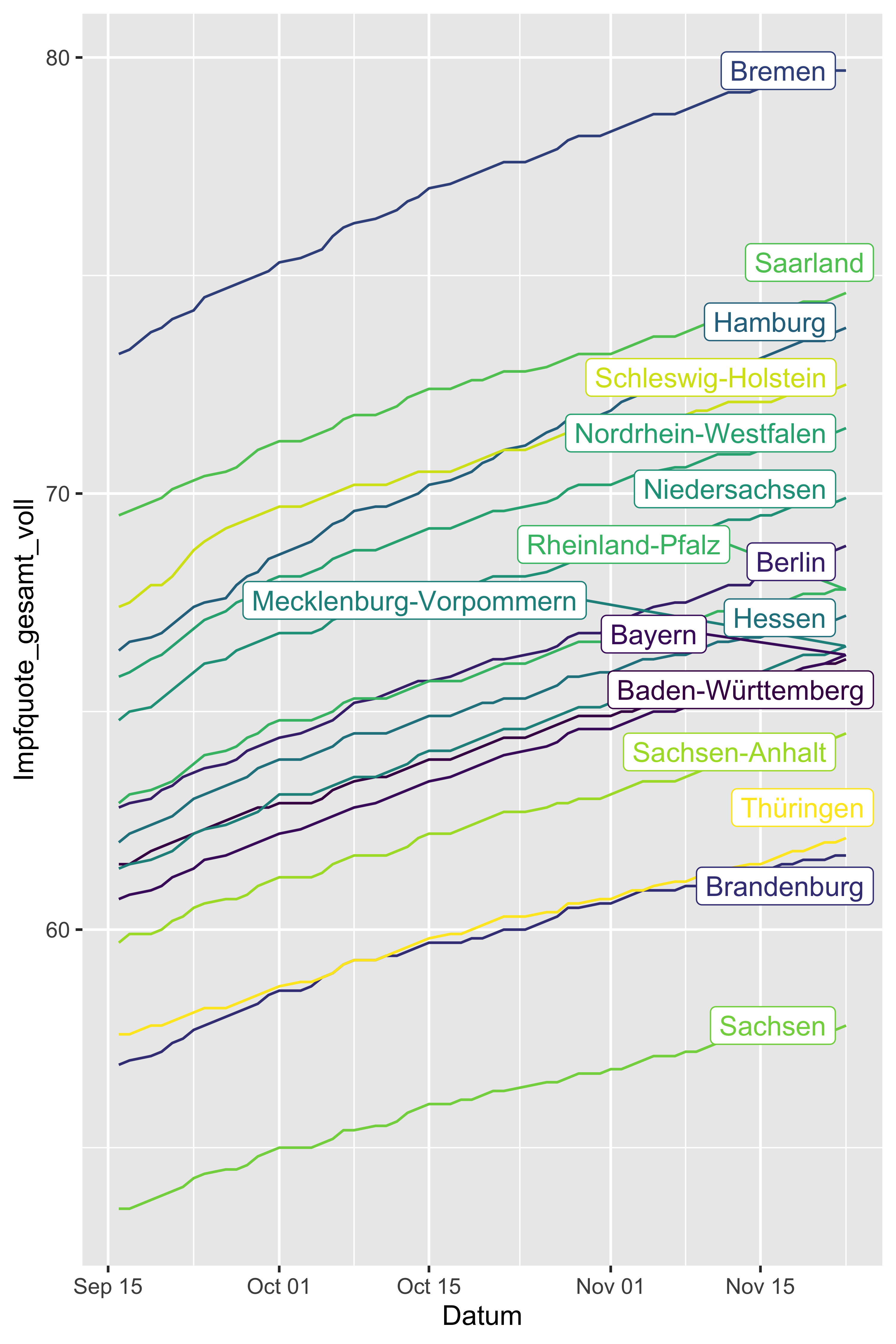
Hm, alles andere als perfekt. Aber lassen wir es damit gut sein und wenden uns wichtigeren Themen zu. Es ist allzu leicht, sich in (vielleicht ganz unterhaltsamen) Details zu verstricken.
Hier gibt es noch ein interessantes Paket, um Liniendiagramme mit Labels zu versehen.
Probieren wir das doch mal aus:
vacc_time_df %>%
filter(Bundesland != "Deutschland") %>%
ggplot() +
aes(x = Datum,
y = Impfquote_gesamt_voll,
color = Bundesland) +
geom_line() +
scale_x_date(limits = c(min(vacc_time_df$Datum),
max(vacc_time_df$Datum)+30)) +
scale_color_viridis_d(breaks = NULL) +
geom_dl(aes(label = Bundesland),
method = list(dl.trans(x = x + 0.2), "last.points", cex = 0.8)) 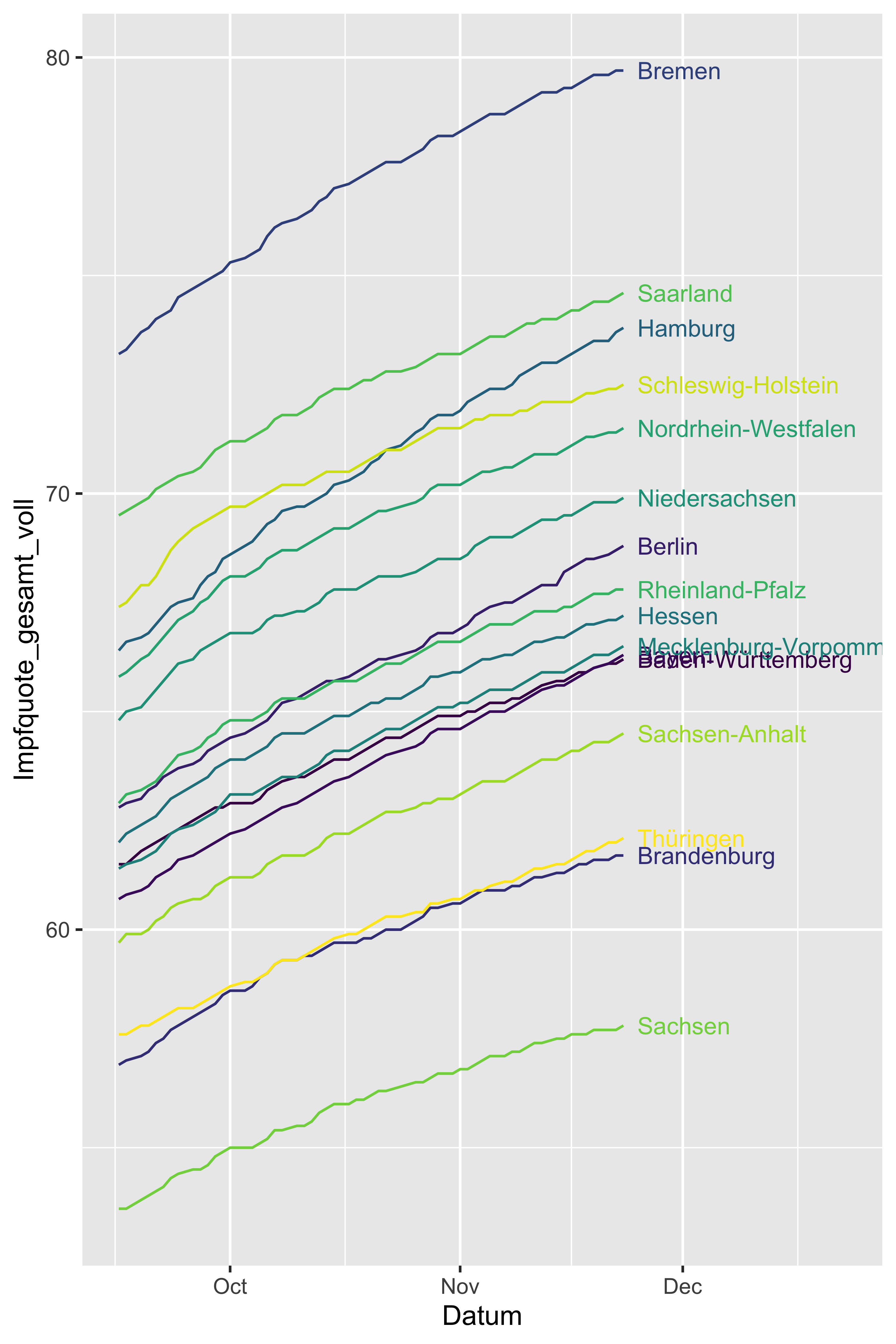
6 Daten joinen
“Verheiraten” wir die Daten zu Impfquoten und Hospitalisierungen.
Das geht mit einem join.
Das Argument by gibt den “Schlüssel” (ID) an,
anhand dessen Zeilen aus den beiden Tabellen “verheiratet” werden.
Hier findet sich eine gute visuelle Erklärung.
hosp_vacc <-
hosp_latest %>%
inner_join(vacc_latest %>% select(-c(Bundesland, Datum)),
by = c("Bundesland_Id" = "BundeslandId_Impfort"))Beim inner_join werden nur Zeilen übernommen,
für die es in beiden Tabellen eine Entsprechung (einen Wert für die ID-Variable) gibt.
7 Zusammenhangsanalysen
Vielleicht ist der wichtigste Hinweis an dieser Stelle, dass Beobachtungsdaten (also nicht von guten Experimenten stammend) keine Aussagen über Kausaleinflüsse erlauben - oder nur unter starken Annahmen.
7.1 Zusammenhang von Impfquote und Hospitalisierung
7.1.1 Im Zeitverlauf
Hier stellt sich die Frage, auf welchen Zeitrahmen wir aggregieren, um eine Korrelation zu berechnen? Je kürzer der Zeitrahmen, desto instabiler die Schätzwerte. Je länger der Zeitrahmen, desto mehr werden Veränderungen im Zeitverlauf unter den Teppich gekehrt. In so einer Situation ist es vielleicht am besten, sich den Koeffizienten in hoher zeitlicher Auflösung anzuschauen, um dann zu entscheiden, wie sehr man aggregieren kann.
korr_vacc_hosp <-
hosp_vacc %>%
select(Jahr,
Woche, Impfquote_gesamt_voll,
Inz_7T_Hosp = `7T_Hospitalisierung_Inzidenz`) %>%
filter(Jahr == 2021) %>%
group_by(Woche) %>%
summarise(Korr_Woche = cor(Impfquote_gesamt_voll,
Inz_7T_Hosp))korr_vacc_hosp_joined <-
korr_vacc_hosp %>%
left_join(hosp_vacc %>% select(Datum, Woche, Monat, Quartal)) %>%
group_by(Woche) %>%
filter(row_number() == 1)7.1.1.1 Korrelation nach Woche
korr_vacc_hosp_joined %>%
mutate(Quartal = factor(Quartal)) %>%
ggplot() +
aes(y = Korr_Woche) +
geom_rect(aes(
x = NULL,
y = NULL,
xmin = Woche-1,
xmax = Woche,
ymin = -Inf,
ymax = +Inf,
fill = Quartal),
alpha = .5) +
scale_fill_manual(values = c("grey", "lightgreen", "darkgreen", "indianred4")) +
geom_hline(yintercept = 0, color = "white", size = 2) +
geom_point(alpha = .7, aes(x = Woche)) +
geom_line(aes(x = Woche)) +
labs(title = "Korrelation von Hospitalisierung und Impfquote pro Woche",
caption = "Quartale des Jahres 2021 sind eingefärbt. Datenquelle: RKI",
x = "Kalenderwoche 2021",
y = "Korrelation (Wochenbasis)")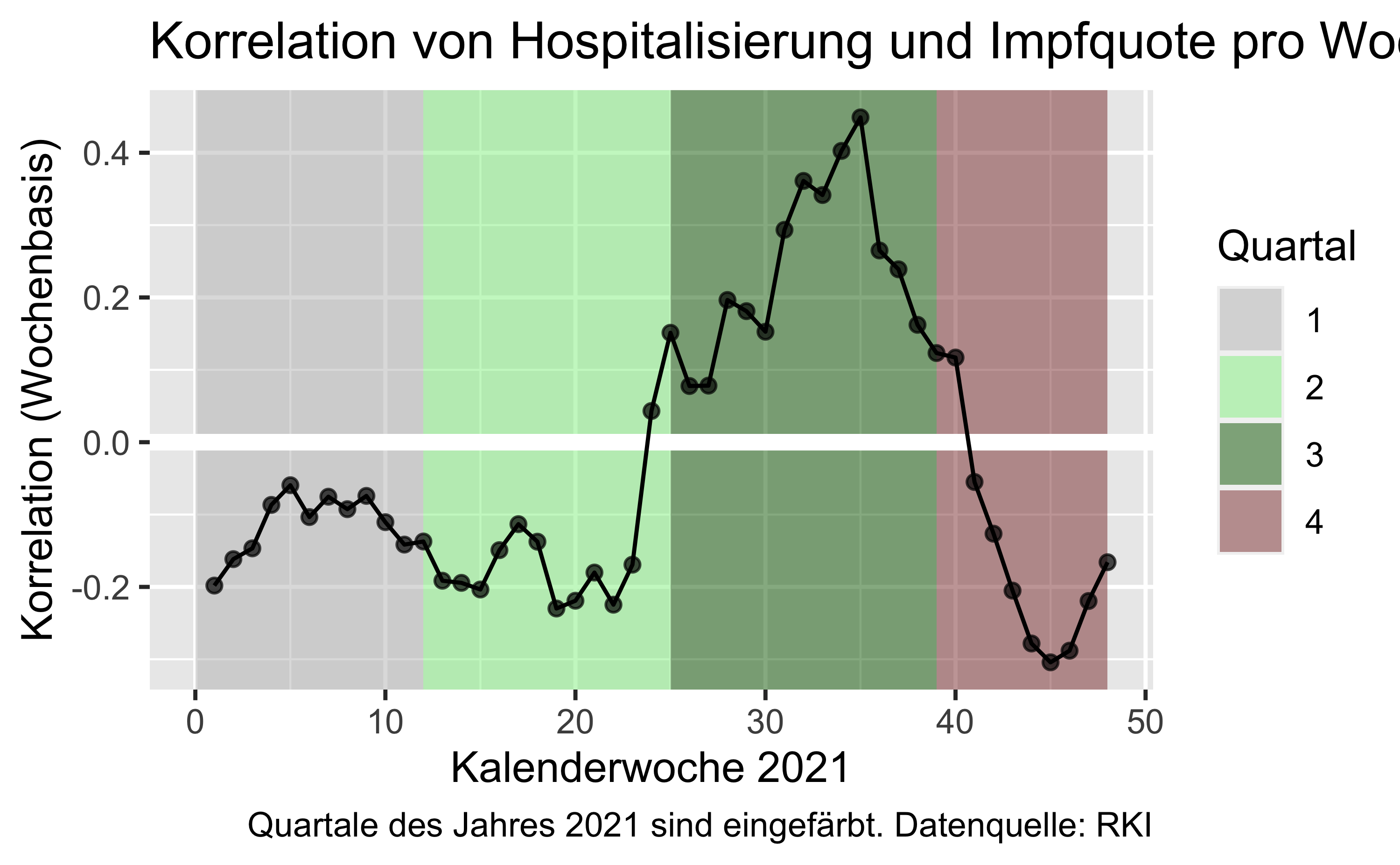
Die positive Korrelation im Sommer 2021 - je mehr Impfung, desto mehr Hospitalisierung - ist vor dem Hintergrund der extrem niedrigen Inzidenzzahlen in dieser Zeit zu sehen.
7.1.1.2 Korrelation nach Monat
korr_vacc_hosp_monat <-
hosp_vacc %>%
select(Jahr,
Monat,
Impfquote_gesamt_voll,
Inz_7T_Hosp = `7T_Hospitalisierung_Inzidenz`) %>%
filter(Jahr == 2021) %>%
group_by(Monat) %>%
summarise(Korr_Monat = cor(Impfquote_gesamt_voll,
Inz_7T_Hosp))korr_vacc_hosp_monat %>%
gt() %>%
fmt_number(2, decimals = 2)| Monat | Korr_Monat |
|---|---|
| 1 | −0.14 |
| 2 | −0.08 |
| 3 | −0.13 |
| 4 | −0.17 |
| 5 | −0.17 |
| 6 | −0.05 |
| 7 | 0.15 |
| 8 | 0.33 |
| 9 | 0.21 |
| 10 | −0.12 |
| 11 | −0.26 |
korr_vacc_hosp_monat_joined <-
korr_vacc_hosp_monat %>%
left_join(hosp_vacc %>% select(Datum, Monat, Quartal)) %>%
group_by(Monat) %>%
filter(row_number() == 1)korr_vacc_hosp_monat_joined %>%
mutate(Quartal = factor(Quartal)) %>%
ggplot() +
aes(y = Korr_Monat) +
geom_rect(aes(
x = NULL,
y = NULL,
xmin = Monat-1,
xmax = Monat,
ymin = -Inf,
ymax = +Inf,
fill = Quartal),
alpha = .5) +
scale_fill_manual(values = c("grey", "lightgreen", "darkgreen", "indianred4")) +
geom_hline(yintercept = 0, color = "white", size = 2) +
geom_point(alpha = .7, aes(x = Monat)) +
geom_line(aes(x = Monat)) +
labs(title = "Korrelation von Hospitalisierung und Impfquote pro Monat",
caption = "Quartale des Jahres 2021 sind eingefärbt. Datenquelle: RKI",
x = "Kalenderwoche 2021",
y = "Korrelation (Wochenbasis)")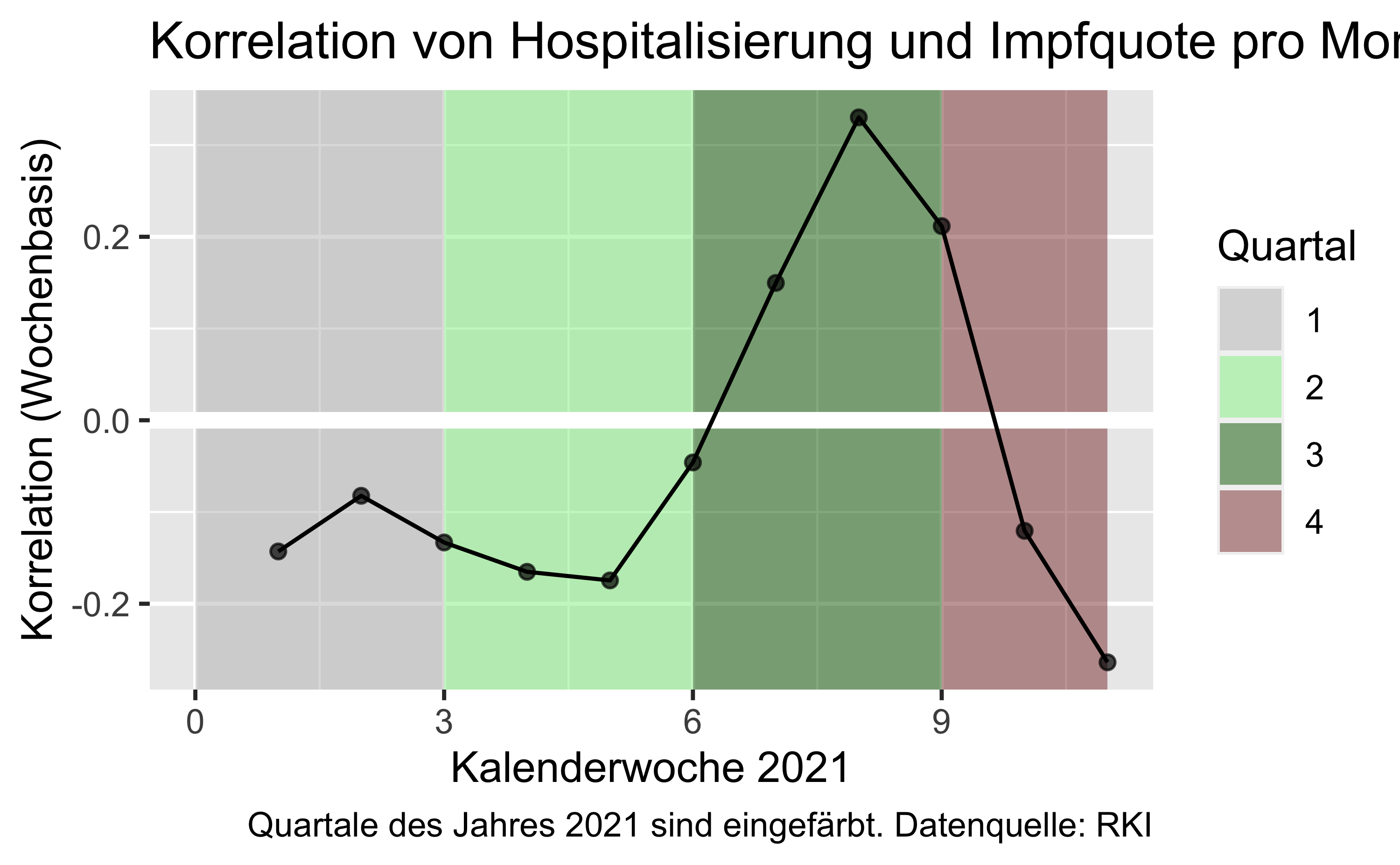
Insgesamt ergibt sich ein ähnliches Bild, wenn man noch Monat oder nach Woche aggregiert und dann die Korrelation jeweils berechnet.
7.1.2 Korrelation nach Bundesland
7.1.2.1 November 2021
hosp_vacc %>%
filter(Monat == 11, Bundesland != "Bundesgebiet") %>%
select(I = Impfquote_gesamt_voll,
H = `7T_Hospitalisierung_Inzidenz`,
B = Bundesland) %>%
group_by(B) %>%
summarise(I = mean(I),
H = mean(H)) %>%
ggplot() +
aes(x = I,
y = H) +
geom_point() +
geom_smooth(method = "lm") +
labs(x = "Impfquote (vollständig)",
y = "7Tage-Hospitalisierungsquote",
title = "Zusammenhang von Impfen und Hospitalisierung",
subtitle = "Daten für November 2021, alle Altersgruppe",
caption = "Datenquelle: RKI")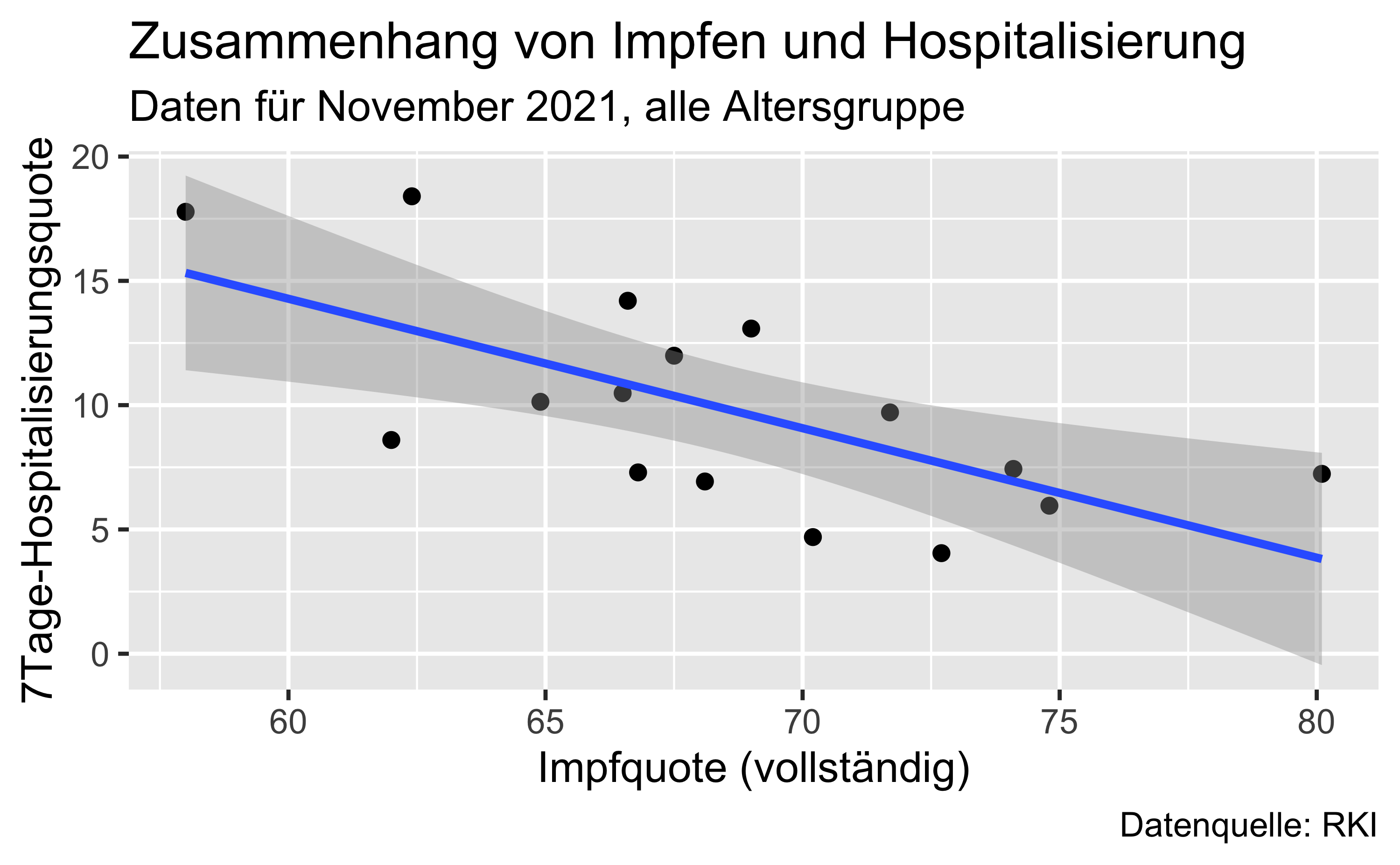
Fügen wir noch die Namen der Bundesländer zu den Punkten hinzu, aber vielleicht besser die Kurzform der Namen.
state_names <-
tibble::tribble(
~Bundesland, ~Kurzform, ~state,
"Deutschland", "DE", "Germany",
"Baden-Württemberg", "BW", "Baden-Württemberg",
"Bayern", "BY", "Bavaria (FreeState)",
"Berlin", "BE", "Berlin",
"Brandenburg", "BB", "Brandenburg",
"Bremen", "HB", "Bremen (Hanseatic City)",
"Hamburg", "HH", "Hamburg (Hanseatic City)",
"Hessen", "HE", "Hesse",
"Mecklenburg-Vorpommern", "MV", "Mecklenburg-Western Pomerania",
"Niedersachsen", "NI", "Lower Saxony",
"Nordrhein-Westfalen", "NW", "North Rhine-Westphalia",
"Rheinland-Pfalz", "RP", "Rhineland-Palatinate",
"Saarland", "SL", "Saarland",
"Sachsen", "SN", "Saxony (Free tate)",
"Sachsen-Anhalt", "ST", "Saxony-Anhalt",
"Schleswig-Holstein", "SH", "Schleswig-Holstein",
"Thüringen", "TH", "Thuringia (Free State)",
"Bundesgebiet", "De", "Federal area"
)state_names %>%
gt()| Bundesland | Kurzform | state |
|---|---|---|
| Deutschland | DE | Germany |
| Baden-Württemberg | BW | Baden-Württemberg |
| Bayern | BY | Bavaria (FreeState) |
| Berlin | BE | Berlin |
| Brandenburg | BB | Brandenburg |
| Bremen | HB | Bremen (Hanseatic City) |
| Hamburg | HH | Hamburg (Hanseatic City) |
| Hessen | HE | Hesse |
| Mecklenburg-Vorpommern | MV | Mecklenburg-Western Pomerania |
| Niedersachsen | NI | Lower Saxony |
| Nordrhein-Westfalen | NW | North Rhine-Westphalia |
| Rheinland-Pfalz | RP | Rhineland-Palatinate |
| Saarland | SL | Saarland |
| Sachsen | SN | Saxony (Free tate) |
| Sachsen-Anhalt | ST | Saxony-Anhalt |
| Schleswig-Holstein | SH | Schleswig-Holstein |
| Thüringen | TH | Thuringia (Free State) |
| Bundesgebiet | De | Federal area |
Joinen wir die Kürzel der Bundesländer:
hosp_vacc2 <-
hosp_vacc %>%
left_join(state_names)hosp_vacc_bundesland_nov <-
hosp_vacc %>%
filter(Monat == 11, Bundesland != "Bundesgebiet") %>%
select(I = Impfquote_gesamt_voll,
H = `7T_Hospitalisierung_Inzidenz`,
Bundesland) %>%
group_by(Bundesland) %>%
summarise(I = mean(I),
H = mean(H)) %>%
left_join(state_names %>% select(-state))
hosp_vacc_bundesland_nov %>%
ggplot() +
aes(x = I,
y = H) +
geom_point(alpha = .5) +
geom_smooth(method = "lm") +
labs(x = "Impfquote (vollständig)",
y = "7Tage-Hospitalisierungsquote",
title = "Zusammenhang von Impfen und Hospitalisierung",
subtitle = "Daten für November 2021, alle Altersgruppe",
caption = "Datenquelle: RKI") +
geom_text(aes(label = Kurzform))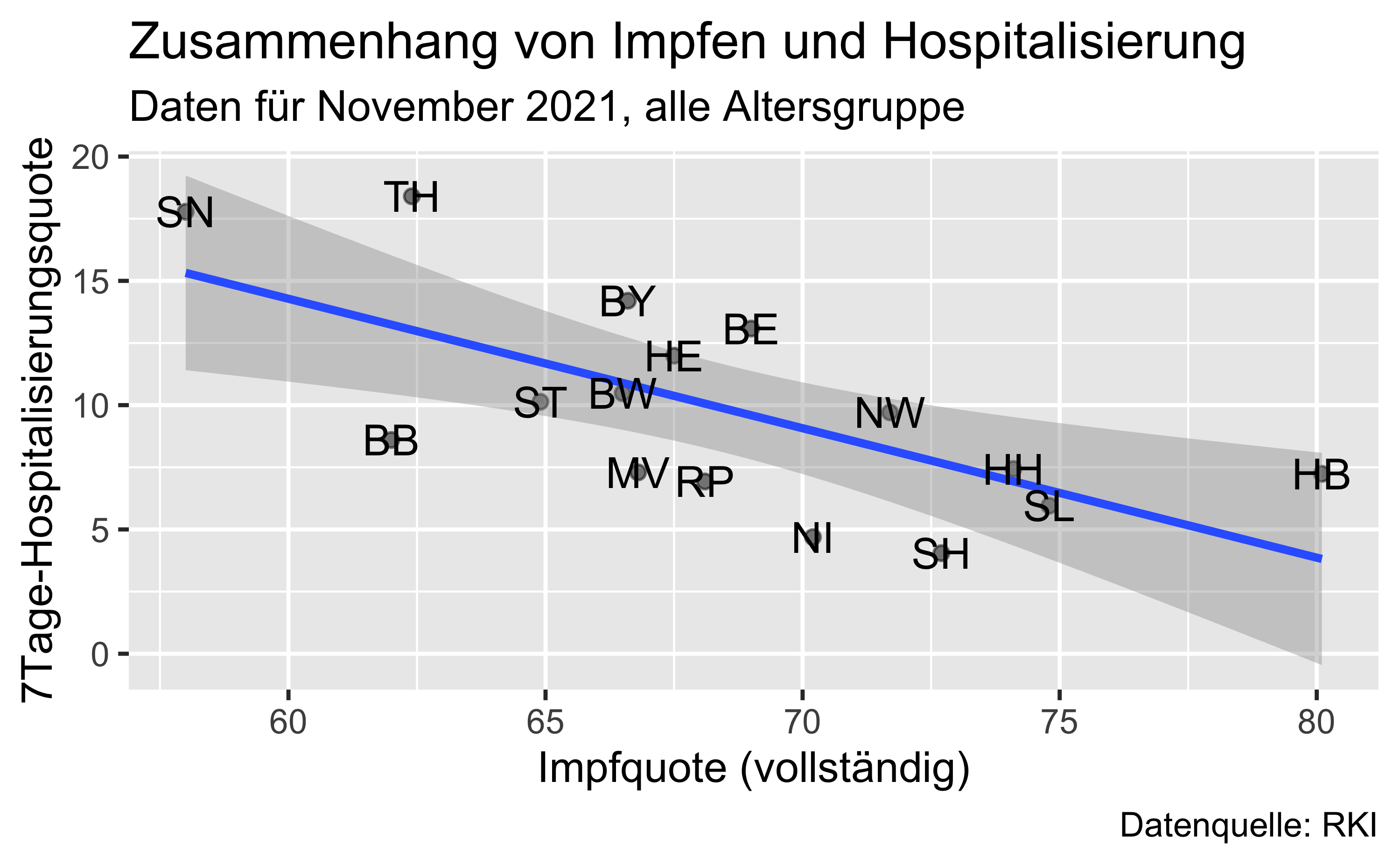
Und so sieht die zugehörige Tabelle aus:
hosp_vacc_bundesland_nov %>%
gt() %>%
fmt_number(3, decimals = 2)| Bundesland | I | H | Kurzform |
|---|---|---|---|
| Baden-Württemberg | 66.5 | 10.48 | BW |
| Bayern | 66.6 | 14.20 | BY |
| Berlin | 69.0 | 13.08 | BE |
| Brandenburg | 62.0 | 8.60 | BB |
| Bremen | 80.1 | 7.24 | HB |
| Hamburg | 74.1 | 7.43 | HH |
| Hessen | 67.5 | 11.99 | HE |
| Mecklenburg-Vorpommern | 66.8 | 7.29 | MV |
| Niedersachsen | 70.2 | 4.69 | NI |
| Nordrhein-Westfalen | 71.7 | 9.71 | NW |
| Rheinland-Pfalz | 68.1 | 6.93 | RP |
| Saarland | 74.8 | 5.95 | SL |
| Sachsen | 58.0 | 17.78 | SN |
| Sachsen-Anhalt | 64.9 | 10.14 | ST |
| Schleswig-Holstein | 72.7 | 4.05 | SH |
| Thüringen | 62.4 | 18.40 | TH |
7.1.3 Pro Quartal
Aggregieren wir den Datensatz pro Quartal und pro Bundesland;:
hosp_vacc_bundesland_pro_Quartal <-
hosp_vacc %>%
filter(Bundesland != "Bundesgebiet") %>%
select(I = Impfquote_gesamt_voll,
H = `7T_Hospitalisierung_Inzidenz`,
Bundesland,
Quartal) %>%
group_by(Bundesland, Quartal) %>%
summarise(I = mean(I),
H = mean(H)) %>%
left_join(state_names)So sieht die zugehörige Tabelle aus (die ersten paar Zeilen)
hosp_vacc_bundesland_pro_Quartal %>%
ungroup() %>%
slice_head(n = 10) %>%
gt() %>%
fmt_number(3, decimals = 2)| Bundesland | Quartal | I | H | Kurzform | state |
|---|---|---|---|---|---|
| Baden-Württemberg | 1 | 66.50 | 7.053471 | BW | Baden-Württemberg |
| Baden-Württemberg | 2 | 66.50 | 4.484780 | BW | Baden-Württemberg |
| Baden-Württemberg | 3 | 66.50 | 1.323548 | BW | Baden-Württemberg |
| Baden-Württemberg | 4 | 66.50 | 9.192524 | BW | Baden-Württemberg |
| Bayern | 1 | 66.60 | 7.431370 | BY | Bavaria (FreeState) |
| Bayern | 2 | 66.60 | 4.507567 | BY | Bavaria (FreeState) |
| Bayern | 3 | 66.60 | 1.351724 | BY | Bavaria (FreeState) |
| Bayern | 4 | 66.60 | 10.679581 | BY | Bavaria (FreeState) |
| Berlin | 1 | 69.00 | 12.197863 | BE | Berlin |
| Berlin | 2 | 69.00 | 3.624239 | BE | Berlin |
Dann updaten wir das letzte Diagramm, nur eben dieses Mal erstellen pro Quartal ein Diagramm.
Zuvor legen wir noch schönere Bezeichnungen der Facetten an, nicht nur 1,2,3,4, sondern “1. Quartal,”2. Quartal” etc.:
Quartal_values <- c("1. Quartal", "2. Quartal",
"3. Quartal", "4. Quartal")
names(Quartal_values) <- c(1:4)Ansonsten ist es das gleiche Vorgehen wie eben auch:
hosp_vacc_bundesland_pro_Quartal %>%
ggplot() +
aes(x = I,
y = H) +
geom_point(alpha = .5) +
geom_smooth(method = "lm") +
labs(x = "Impfquote (vollständig)",
y = "7Tage-Hospitalisierungsquote",
title = "Zusammenhang von Impfen und Hospitalisierung",
subtitle = "Aufgeteilt nach Quartale, aggregiert über alle Altersgruppe",
caption = "Datenquelle: RKI") +
geom_text(aes(label = Kurzform)) +
facet_wrap(~ Quartal, labeller = labeller(Quartal = Quartal_values))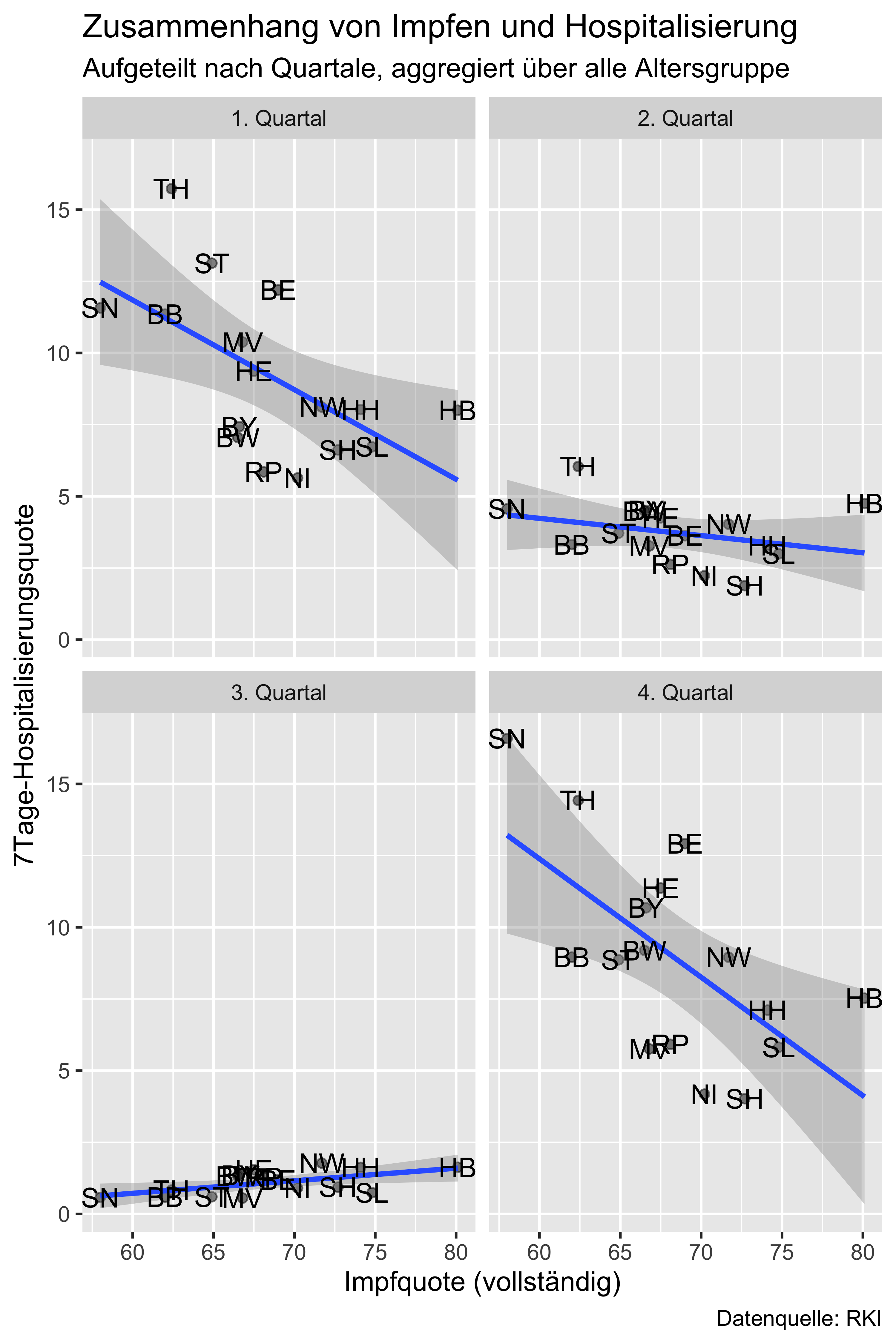
Wir sehen, dass es im 3. Quartal in der Inzidenz kaum Streuung gibt, was die sehr geringe Korrelation erklärt.
8 Fazit zum Zusammenhang von Hospitalisierung und Impfquote
8.1 Deskriptiv
Es fand sich ein negativer Zusammenhang von Hospitalisierung und Impfquote. Nur im Sommer, als die Hospitalisierung praktisch Null war und daher keine Streuung aufwies, fand sich (eine mathematisch notwendige Konsequenz) fast keine Korrelation.
8.2 Aber worum geht es uns eigentlich?
Warum haben wir uns überhaupt für die Frage nach dem Zusammenhang von Impfquote und Hospitalisierung interessiert? Interessiert uns allein der deskriptive Sachverhalt des Kovariierens der beiden Größen? Ich glaube nicht. Wenn wir hören, dass “Störche und Babies korreliert sind”, und vielleicht sogar Schmunzeln beim Gedanken, “wenn es viele Störche gibt, dann gibt es auch viele Babies (und umgekehrt)”, haben wir eine kausale Verbindung, einen ursächlichen Einfluss von Störchen auf Babies im Kopf. Ich meine, nur deswegen finden wir den Zusammenhang interessant. Unser Kopf (unsere Wahrnehmung) hat einen Filter für kausale Einflüsse. Evolutionär kann man das sicher gut erklären: Wenn man weiß, was die Ursache für ein Problem ist, hat bessere Karten, das Problem zu lösen, als derjenige, der keinen Schimmer hat, warum die Dinge gerade schieflaufen. Unser Hirn muss, könnte man aus evolutionäre Sicht behaupten, auf Kausalzusammenhänge getrimmt sein.
Deswegen, meine ich, interessieren wir uns für den Zusammenhang von Impfquote und Inzidenz (der Hospitalisierung). Wir sind, naturgemäß und einsichtigerweise, sehr an dieser Frage interessiert, es ist eine sehr wichtige Frage.
Allerdings: aus Korrelation kann man nicht einfach so Kausalzusammenhänge ableiten.
Anders gesagt, wenn wir - vielleicht nur implizit - glauben, die Impfquote I ist die (eine) Ursache von Hospitalisierung H, haben wir z.B. dieses Kausalmodell im Kopf:
8.2.1 Kausalmodell 1
Kausalmodelle kann man mit Directed Acyclic Graphs (DAGs) darstellen.
Also, ein Modell, das mit unserem impliziten Kausalmodell d’accord geht, sagt, sinngemäß:
“Die Hospitalisierungsquote H wird von der Impfquote H beeinflusst. Natürlich spielen weitere, unbekannte Faktoren U eine Rolle; die haben aber nichts mit H zu tun.”
Als DAG:
dag1 <-
dagitty(
'dag {
I [pos = "0,1"]
H [pos = "1,0"]
U [pos = "0, -1"]
I -> H
U -> H
}
'
)
plot(dag1)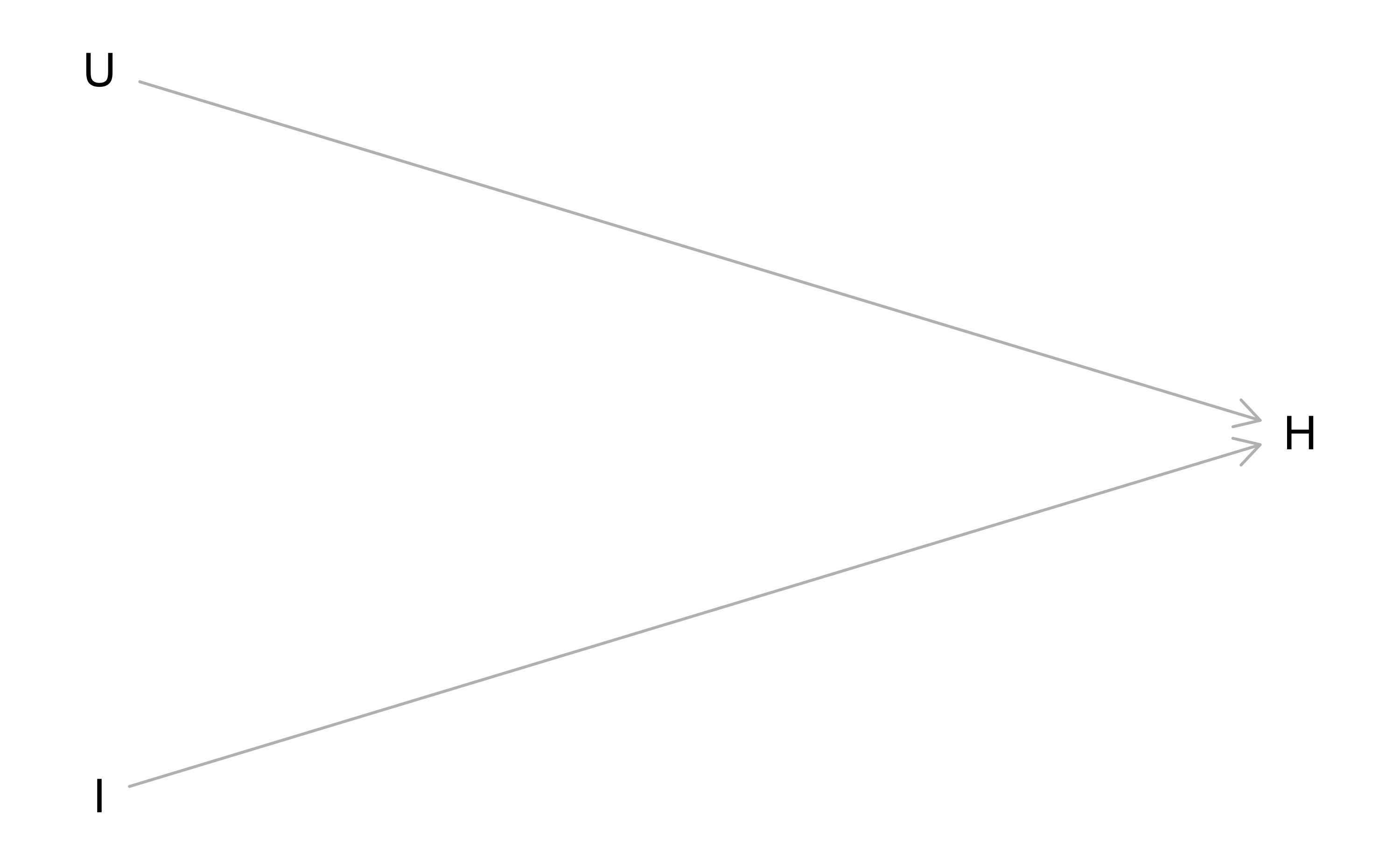
Nur wenn U nichts mit I zu tun hat (zumindest in einem bestimmten Sinn nichts zu tun hat), können wir mit der Korrelation von I und H den kausalen Effekt wahrnehmen, dem wir vermutlich auf der Fährte sind, zumindest ist das ein lohnendes Ziel.
8.2.2 Kausalmodell 2
Allerdings könnte die Wahrheit auch so aussehen:
dag2 <-
dagitty(
'dag {
I [pos = "0,1"]
H [pos = "1,0"]
U1 [pos = "0, -1"]
U2 [pos = "-1,0"]
I -> H
U1 -> H
U2 -> U1
U2 -> I
}
'
)
plot(dag2)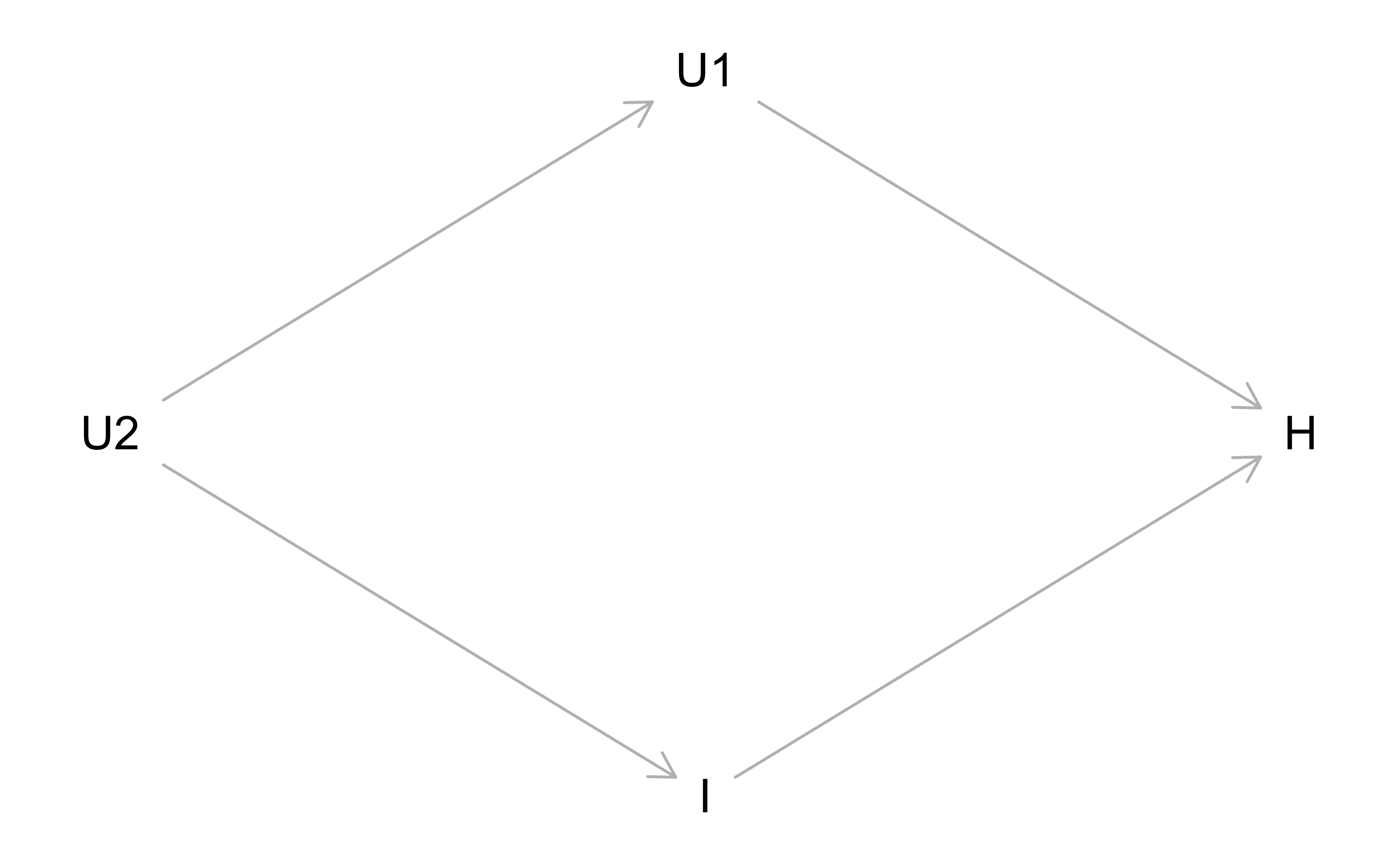
Jetzt ist die Korrelation (allgemeiner: der statistische Zusammenhang) von I mit H nicht mehr so unbedarft. U2 hat seine Finger im Spiel. U1 ist nämlich über U2 (eine weitere unbekannte oder ungemessene Größe) mit I (und weiter nach H) verbunden. Man spricht von einer Konfundierung: In der Assoziation von I mit H mischt sich ein weiterer kausaler Pfad: Der von U1->U2->I->H. Damit ist die Assoziation von I mit H die Summe (oder besser: die Mischung) von zwei Pfaden und man kann nicht ohne Weiteres sagen, welcher Pfad wieviel der Assoziation versursacht. Schlechte Nachrichten. Wenn wir aber U1 und U2 messen können, können wir wiederum Hoffnung schöpfen, die kausalen Pfade klar zu ziehen.
8.2.3 Interpretation hängt vom Kausalmodell ab
Ob wir also diese (oder eine andere) Korrelation interpretieren können (und interpretieren, so glaube ich, ist oft oder in hohem Maße eine kausale Sache) hängt vom Kausalmodell ab, an das wir glauben.
Natürlich sind noch viele andere Kausalmodelle denkbar. Ja, die Sache ist kompliziert.
Das ist übrigens der Grund, warum die Menschen Experimente erfunden haben. Mit Experimenten kann man diese gordischen Kausalknoten durchschneiden, und dann vergleichsweise einfach die Kausalstrukturen klären. Leider sind Experimente nicht immer möglich.
Glücklicherweise im Fall der Frage “Was bringt Impfen gegen Corona?” schon. Da gibt es Experimente, die diese Frage untersuchen. Vermutlich sind diese Studien die besten Möglichkeiten, die kausale Frage nach der Wirksamkeit von Impfung zu klären.
Natürlich, wenn man an ein Kausalmodell glaubt - bzw. es gut begründen kann - das die Vergleichbarkeit der Gruppen nahelegt, dann ist wieder alles gut. Wir wären also zurück beim Kausalmodell 1, oben.
8.3 Wo sind hier die Modelle?
Wäre es jetzt nicht allerhöchste Zeit, mit dem Modellieren anzufangen? Eine paar ausgefeilte Regressionsmodelle zu prüfen? An sich ja. Leider gibt es zwei Probleme. Erstens muss man weitere Daten, also Kennwerte weiterer Messgrößen (Variablen) haben, die man dann in einer multiplen Analyse (eine Regression mit mehreren Prädiktoren) untersuchen kann. Und natürlich nicht irgendwelche Daten, sondern “die richtigen”. Das führt uns zum zweiten Problem. Die verbreitete Praxis, alle Daten, die man hat, in ein Regressionsmodell zu “kippen” und dann das Beste zu hoffen, ist der falsche Weg.
Das Hinzunehmen von Prädiktoren ohne ein stimmiges Kausalmodell kann genauso viel schaden wie nützen.
Anders gesagt: Ohne ein (stimmiges) Kausalmodell kann man sich das Modellieren schenken, wenn es darum geht, “echte Effekte”, Kausaleffekte also, zu schätzen.
Geht es einem hingegen “nur” darum, vorhersagen zu machen, etwa “Wie viele Coronafälle sind für nächste Woche zu erwarten?”, dann ist kein Kausalmodell nötig (obwohl auch nützlich). Vorhersagen kann man anhand rein statistischer Zusammenhänge tätigen. In der Regel geht es einem aber (in solchen Situationen wie der hier untersuchten Forschungsfrage) um kausale Fragen, die ohne ein Kausalmodell kaum zu beantworten sind.
Natürlich könnte man argumentieren, ein Kausalmodell sei einem wurscht, man will sich nur an den statistischen Zusammenhängen erfreuen. So eine Behauptung gleicht der Aussage, man interessiere sich “einfach so” für den Zusammenhang von Störchen und Babies.

Quelle: Herbert Kuhl, Wikimedia
Etwas Googeln liefert ein paar weitere schöne Beispiele für Korrelationen ohne Anspruch an Kausalität:
- Höhe des Deutschen Meisters im Stabhochsprung bei den Deutschen Hallenmeisterschaften und Anzahl der für Versuche und andere wissenschaftliche Zwecke verwendeten Kaninchen
- Geldvermögen der privaten Haushalte (orange) und Zahl der Patienten, die aus Krankenhäusern entlassen wurden und bei denen “Bestimmte infektiöse und parasitäre Krankheiten” diagnostiziert wurden
- Beschäftigte auf Campingplätzen und Erntemenge von Gurken auf dem Freiland
In allen diesen Beispielen fand sich eine (fast) perfekte Korrelation (0.9-1). Es fällt mir schwer, mir vorzustellen, dass man sich “rein deskriptiv” für diese Zusammenhänge interessiert.
Kurz gesagt: Modellieren macht nur Sinn, wenn man ein Kausalmodell hat; zumindest wenn man eine kausale Frage beantworten möchte.
Ich will nicht abstreiten, dass es hier nicht möglich wäre, ein stimmiges Kausalmodell zu erstellen. Allerdings ist sehr viel mehr Wissen nötig als eine einfache Korrelation.
Für die Zwecke dieser Fallstudie lassen wir es an dieser Stelle bewenden.
8.4 Interpretation hängt von der gesamten Befundlage ab
Eine schwierige Frage zu beantworten sollte nicht auf Basis einer einzelnen Studie, gerade wenn diese verschiedene Kausalinterpretationen erlaubt, passieren. Die “Gesamtantwort” muss im Lichte der Zusammenschau aller verfügbaren Ergebnissen geschehen. Das ist das Gleiche wie zu sagen, dass man ein Puzzle nicht anhand eines einzelnen Puzzlestücks einschätzen kann (in aller Regel).
Was die Wirksamkeit der Corona-Impfung betrifft, sprechen die verfügbaren Daten, vor allem die aus hoch qualitativen Studien, zugunsten der Wirksamkeit der Impfung.
Beispiele für hoch qualitative Studien zur Wirksamkeit der Corona-Impfung sind z.B. hier zu finden.
Leider ist Corona so eine Art Puzzle, das (durch Mutationen des Genoms) seine Form andauernd und vielleicht sogar massiv ändern kann. Und natürlich sind noch viele Fragen zur Biologie des Virus offen. So muss ein Fazit in diesem wie in vielen Fällen vorläufig bleiben.
Immerhin haben wir die Impfung, die, in Zusammenschau der verfügbaren Daten, offenbar - Stand heute - hoch wirksam ist. In so kurzer Zeit eine so wirksame Therapie entwickelt zu haben, ist vermutlich ein großer, vielleicht historischer Erfolg, der Wissenschaft.
8.5 Notiz zum Umgang mit Fehlinformationen
Leider kursieren eine Menge von Fehlinformationen zum Thema Corona-Impfung (im Internet). Eine ausführliche Beschäftigung damit würde den Rahmen dieses Posts sprengen. Nur zwei Notizen zu den Methoden, die gerne verwendet werden. Zum einen wird ein Befund herausgegriffen und verabsolutiert. Es wird nicht versucht, eine Zusammenschau von Informationen anzustrengend. Zum anderen wird gerne ein “Fakt” berichtet - etwa zur Frage, wie wirksam eine Corona-Impfung ist, der zwar nicht falsch ist, aber Wesentliches außen vor lässt. So wird vielleicht von einer möglichen Ursache gesprochen, aber eine zweite außen vorgelassen. Oder es wird von einem Fall mit schweren Nebenwirkungen einer Impfung berichtet, aber nicht davon, dass eine viel größere Zahl von Menschenleben durch die Impfung gerettet wurde.
Zum Glück gibt es auch viele gute Berichtserstattung, z.B. - eine Replik auf einen Fall ähnlich gelagert zu dem gerade Beschriebenen - hier.
9 sessionInfo
sessioninfo::session_info()## ─ Session info ───────────────────────────────────────────────────────────────
## setting value
## version R version 4.1.0 (2021-05-18)
## os macOS Big Sur 10.16
## system x86_64, darwin17.0
## ui X11
## language (EN)
## collate en_US.UTF-8
## ctype en_US.UTF-8
## tz Europe/Berlin
## date 2021-12-09
##
## ─ Packages ───────────────────────────────────────────────────────────────────
## package * version date lib source
## abind 1.4-5 2016-07-21 [1] CRAN (R 4.1.0)
## assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.1.0)
## backports 1.2.1 2020-12-09 [1] CRAN (R 4.1.0)
## blogdown 1.4 2021-07-23 [2] CRAN (R 4.1.0)
## bookdown 0.24.2 2021-10-15 [1] Github (rstudio/bookdown@ba51c26)
## boot 1.3-28 2021-05-03 [2] CRAN (R 4.1.0)
## broom 0.7.9 2021-07-27 [1] CRAN (R 4.1.0)
## bslib 0.3.1 2021-10-06 [1] CRAN (R 4.1.0)
## car 3.0-11 2021-06-27 [2] CRAN (R 4.1.0)
## carData 3.0-4 2020-05-22 [2] CRAN (R 4.1.0)
## cellranger 1.1.0 2016-07-27 [1] CRAN (R 4.1.0)
## cli 3.1.0 2021-10-27 [1] CRAN (R 4.1.0)
## colorspace 2.0-2 2021-06-24 [1] CRAN (R 4.1.0)
## corrr * 0.4.3 2020-11-24 [2] CRAN (R 4.1.0)
## crayon 1.4.2 2021-10-29 [1] CRAN (R 4.1.0)
## crul 1.1.0 2021-02-15 [1] CRAN (R 4.1.0)
## curl 4.3.2 2021-06-23 [1] CRAN (R 4.1.0)
## dagitty * 0.3-1 2021-01-21 [1] CRAN (R 4.1.0)
## data.table 1.14.2 2021-09-27 [1] CRAN (R 4.1.0)
## DBI 1.1.1 2021-01-15 [1] CRAN (R 4.1.0)
## dbplyr 2.1.1 2021-04-06 [1] CRAN (R 4.1.0)
## digest 0.6.28 2021-09-23 [1] CRAN (R 4.1.0)
## directlabels * 2021.1.13 2021-01-16 [1] CRAN (R 4.1.0)
## dplyr * 1.0.7 2021-06-18 [1] CRAN (R 4.1.0)
## DT 0.19.1 2021-10-15 [1] Github (rstudio/DT@e223814)
## ellipsis 0.3.2 2021-04-29 [1] CRAN (R 4.1.0)
## evaluate 0.14 2019-05-28 [1] CRAN (R 4.1.0)
## fansi 0.5.0 2021-05-25 [1] CRAN (R 4.1.0)
## fastmap 1.1.0 2021-01-25 [2] CRAN (R 4.1.0)
## forcats * 0.5.1 2021-01-27 [1] CRAN (R 4.1.0)
## foreign 0.8-81 2020-12-22 [2] CRAN (R 4.1.0)
## fs 1.5.0 2020-07-31 [1] CRAN (R 4.1.0)
## generics 0.1.1 2021-10-25 [1] CRAN (R 4.1.0)
## ggplot2 * 3.3.5 2021-06-25 [1] CRAN (R 4.1.0)
## ggrepel * 0.9.1 2021-01-15 [2] CRAN (R 4.1.0)
## glue 1.5.1 2021-11-30 [1] CRAN (R 4.1.0)
## gt * 0.3.1 2021-08-07 [1] CRAN (R 4.1.0)
## gtable 0.3.0 2019-03-25 [1] CRAN (R 4.1.0)
## haven 2.4.1 2021-04-23 [1] CRAN (R 4.1.0)
## hms 1.1.1 2021-09-26 [1] CRAN (R 4.1.0)
## htmltools 0.5.2 2021-08-25 [1] CRAN (R 4.1.0)
## htmlwidgets 1.5.4 2021-09-08 [1] CRAN (R 4.1.0)
## httpcode 0.3.0 2020-04-10 [1] CRAN (R 4.1.0)
## httpuv 1.6.3 2021-09-09 [1] CRAN (R 4.1.0)
## httr 1.4.2 2020-07-20 [1] CRAN (R 4.1.0)
## jquerylib 0.1.4 2021-04-26 [1] CRAN (R 4.1.0)
## jsonlite 1.7.2 2020-12-09 [1] CRAN (R 4.1.0)
## knitr 1.36 2021-09-29 [1] CRAN (R 4.1.0)
## later 1.3.0 2021-08-18 [1] CRAN (R 4.1.0)
## lifecycle 1.0.1 2021-09-24 [1] CRAN (R 4.1.0)
## lubridate * 1.7.10 2021-02-26 [1] CRAN (R 4.1.0)
## magrittr 2.0.1 2020-11-17 [1] CRAN (R 4.1.0)
## MASS 7.3-54 2021-05-03 [2] CRAN (R 4.1.0)
## mime 0.12 2021-09-28 [1] CRAN (R 4.1.0)
## miniUI 0.1.1.1 2018-05-18 [1] CRAN (R 4.1.0)
## modelr 0.1.8 2020-05-19 [1] CRAN (R 4.1.0)
## munsell 0.5.0 2018-06-12 [1] CRAN (R 4.1.0)
## openxlsx 4.2.3 2020-10-27 [1] CRAN (R 4.1.0)
## pillar 1.6.4 2021-10-18 [1] CRAN (R 4.1.0)
## pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.1.0)
## plyr 1.8.6 2020-03-03 [1] CRAN (R 4.1.0)
## promises 1.2.0.1 2021-02-11 [2] CRAN (R 4.1.0)
## purrr * 0.3.4 2020-04-17 [1] CRAN (R 4.1.0)
## quadprog 1.5-8 2019-11-20 [1] CRAN (R 4.1.0)
## R6 2.5.1 2021-08-19 [1] CRAN (R 4.1.0)
## Rcpp 1.0.7 2021-07-07 [1] CRAN (R 4.1.0)
## rcrossref * 1.1.0 2020-10-02 [1] CRAN (R 4.1.0)
## readr * 2.0.0 2021-07-20 [1] CRAN (R 4.1.0)
## readxl 1.3.1 2019-03-13 [1] CRAN (R 4.1.0)
## reprex 2.0.0 2021-04-02 [1] CRAN (R 4.1.0)
## rio 0.5.26 2021-03-01 [1] CRAN (R 4.1.0)
## rlang 0.4.12 2021-10-18 [1] CRAN (R 4.1.0)
## rmarkdown 2.11 2021-09-14 [1] CRAN (R 4.1.0)
## rstatix * 0.7.0 2021-02-13 [1] CRAN (R 4.1.0)
## rstudioapi 0.13 2020-11-12 [1] CRAN (R 4.1.0)
## rvest 1.0.0 2021-03-09 [1] CRAN (R 4.1.0)
## sass 0.4.0 2021-05-12 [1] CRAN (R 4.1.0)
## scales 1.1.1 2020-05-11 [1] CRAN (R 4.1.0)
## sessioninfo 1.1.1 2018-11-05 [2] CRAN (R 4.1.0)
## shiny 1.7.1 2021-10-02 [1] CRAN (R 4.1.0)
## stringi 1.7.5 2021-10-04 [1] CRAN (R 4.1.0)
## stringr * 1.4.0 2019-02-10 [1] CRAN (R 4.1.0)
## tibble * 3.1.6 2021-11-07 [1] CRAN (R 4.1.0)
## tictoc * 1.0.1 2021-04-19 [2] CRAN (R 4.1.0)
## tidyr * 1.1.4 2021-09-27 [1] CRAN (R 4.1.0)
## tidyselect 1.1.1 2021-04-30 [1] CRAN (R 4.1.0)
## tidyverse * 1.3.1 2021-04-15 [1] CRAN (R 4.1.0)
## tzdb 0.1.2 2021-07-20 [2] CRAN (R 4.1.0)
## utf8 1.2.2 2021-07-24 [1] CRAN (R 4.1.0)
## V8 3.4.2 2021-05-01 [1] CRAN (R 4.1.0)
## vctrs 0.3.8 2021-04-29 [1] CRAN (R 4.1.0)
## withr 2.4.2 2021-04-18 [1] CRAN (R 4.1.0)
## xfun 0.28 2021-11-04 [1] CRAN (R 4.1.0)
## xml2 1.3.2 2020-04-23 [1] CRAN (R 4.1.0)
## xtable 1.8-4 2019-04-21 [1] CRAN (R 4.1.0)
## yaml 2.2.1 2020-02-01 [1] CRAN (R 4.1.0)
## zip 2.2.0 2021-05-31 [2] CRAN (R 4.1.0)
##
## [1] /Users/sebastiansaueruser/Library/R/x86_64/4.1/library
## [2] /Library/Frameworks/R.framework/Versions/4.1/Resources/library