1 Setup

library(tidyverse)
library(mosaic)
library(testthat)
library(magrittr)
library(sessioninfo)
library(rstanarm)

2 Fallbeispiel

Im Statistikskript der FOM-Hochschule (entwickelt vom ifes) wird folgendes Beispiel zur Einführung von simulationsbasierter Inferenz verwendet:

Im Rahmen einer Sonderveranstaltung der FOM Dortmund (6.10.2016) 102 und Münster (9.11.2017) tippten von n = 34 Teilnehmer*innen x = 12 im Rahmen eines Dreieckstest auf die richtige Probe, d. h. das andere Bier.

Wandeln wir die Daten leicht ab (dann geht es schöner auf).

Also sagen wir:

n <- 36
x <- 14
prob_null <- 1/3

Aus Gründen der Konvergenz vergrößern wir die Stichprobe noch einmal:

n2 <- n * 10
x2 <- x * 10

3 Datensatz

Erstellen wir eine Funktion, die einen Datensatz, in Abhängigkeit gewählter Parameter \(n\) und \(x\) erstellt.

3.1 Funktion, um Daten zu simulieren

bier_data <- function(n, x) {
  # n: sample size
  # x: successes
  # This function generates data for Bernoulli chain data
    out <-
    tibble(id = 1:n,
           success = c(rep.int(1, x), rep.int(0, n-x)))

  return(out)
}

Probieren wir’s aus.

3.1.1 Kleine Stichprobe

d <- bier_data(n = n, x = x)

glimpse(d)
#> Rows: 36
#> Columns: 2
#> $ id      <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18,…
#> $ success <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0,…

3.1.2 Große Stichprobe

d2 <- bier_data(n = n2, x = x2)

3.2 Unit Testing

Im Sinne des Test-Driven-Designs: Schreiben wir zuerst einen Unit Test (oder mehrere) für die geplante (noch nicht geschriebene!) Funktion zur Erstellung der (simulierten) Daten.

test_that("Datensatz in Abhängigkeit von n und x erstellt",
          {
            expect_equivalent(nrow(bier_data(34, 12)), 34)
            expect_equivalent(sum(bier_data(34,12)$success), 12)
          })
#> Test passed 🥇

4 Signifikanz-Tests

\[H_0: \pi = 1/3\] \[H_A: \pi \ne 1/3\]

Wir testen also ungerichtet.

\(\pi=1/3\) rührt daher, dass es drei Optionen gibt und nur eine davon ist ein Treffer.

4.1 Simulationsbasierte Inferenz (SBI)

4.1.1 Kleine Stichprobe

set.seed(1896) 
Nullvtlg <- do(10000) * rflip(n = n, prob = prob_null)

glimpse(Nullvtlg)
#> Rows: 10,000
#> Columns: 4
#> $ n     <dbl> 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, …
#> $ heads <dbl> 10, 11, 9, 14, 10, 8, 13, 15, 8, 19, 11, 13, 10, 15, 15, 15, 14,…
#> $ tails <dbl> 26, 25, 27, 22, 26, 28, 23, 21, 28, 17, 25, 23, 26, 21, 21, 21, …
#> $ prop  <dbl> 0.2777778, 0.3055556, 0.2500000, 0.3888889, 0.2777778, 0.2222222…

Berechnen wir \(\bar{\pi}\):

propdach <- sum(d$success) / nrow(d)
propdach
#> [1] 0.3888889

Mit Methoden des tidyverse ist es umständlicher, propdach zu berechnen; das tidyverse ist für die Arbeit mit Tabellen ausgelegt, nicht für einzelne Werte (oder Vektoren).

Die Abweichung von prob_null in der Stichprobe beträgt:

abw_stipro <- abs(propdach - prob_null)
abw_stipro
#> [1] 0.05555556

Diese Abweichung fügen wir bei jeder simulierten Stichprobe hinzu:

Nullvtlg <-
  Nullvtlg %>% mutate(abw = abs(prop - prob_null))

pvalue_simu1 <- prop( ~ (abw >= abw_stipro),
                 data = Nullvtlg)
pvalue_simu1
#> prop_TRUE 
#>    0.4872

4.1.2 Große Stichprobe

Für die große Stichprobe analog:

set.seed(1896) 
Nullvtlg2 <- do(10000) * rflip(n = n2, prob = prob_null)

Nullvtlg2 <-
  Nullvtlg2 %>% mutate(abw = abs(prop - prob_null))

pvalue_simu2 <- prop( ~ (abw >= abw_stipro),
                 data = Nullvtlg2)
pvalue_simu2
#> prop_TRUE 
#>    0.0261

4.2 \(\chi^2\)-Test

Man beachte, dass der \(\chi^2\)-Test nur zweiseitig testet.

4.2.1 Kleine Stichprobe

success_freq <- table(d$success)
success_freq
#> 
#>  0  1 
#> 22 14

success_prob <- c(1 - prob_null, prob_null)

pvalue_chi1 <- chisq.test(x = success_freq,
           p = success_prob
           )$p.value 

pvalue_chi1
#> [1] 0.4795001

4.2.2 Große Stichprobe

pvalue_chi2 <- 
  chisq.test(x = table(d2$success),
             p = success_prob)$p.value

pvalue_chi2
#> [1] 0.02534732

4.3 Binomialtest

4.3.1 kleine Stichprobe

pvalue_binom1 <- binom.test(x = x,
                            n = n,
                            p = prob_null)$p.value
pvalue_binom1
#> [1] 0.4829805

Von Hand:

Der Erwartungswert \(\mathbb{E}\) einer binomialverteilten Zufallsvariablen ist so definiert:

\(\mathbb{E} = np\), mit \(n\) der Anzahl der Versuche und \(p\) der Trefferwahrscheinlichkeit.

\(E(X) = n * 1/3\)

E_X <- n * 1/3
E_X
#> [1] 12

Der Varianz \(\mathbb{V}\) einer binomialverteilten Zufallsvariablen ist so definiert:

\(\mathbb{V} = npq\), mit \(q=p-1\).

Var_X = n * 1/3 * 2/3
Var_X
#> [1] 8

Bei genügend großen Stichproben ist \(X\) normalverteilt, daher lässt sich ein z-Wert berechnen:

z <- (x - E_X) / sqrt(Var_X)
z
#> [1] 0.6666667

Also beträgt der p-Wert:

1 - pnorm(q = z)
#> [1] 0.2524925

4.3.2 Große Stichprobe

pvalue_binom2 <- binom.test(x = x2,
                            n = n2,
                            p = prob_null)$p.value
pvalue_binom2
#> [1] 0.0290804

4.4 Logistische Regression

glm1 <- glm(success ~ 1, 
            data = d,
            family = "binomial")
glm1 %>% summary()
#> 
#> Call:
#> glm(formula = success ~ 1, family = "binomial", data = d)
#> 
#> Deviance Residuals: 
#>     Min       1Q   Median       3Q      Max  
#> -0.9925  -0.9925  -0.9925   1.3744   1.3744  
#> 
#> Coefficients:
#>             Estimate Std. Error z value Pr(>|z|)
#> (Intercept)  -0.4520     0.3419  -1.322    0.186
#> 
#> (Dispersion parameter for binomial family taken to be 1)
#> 
#>     Null deviance: 48.114  on 35  degrees of freedom
#> Residual deviance: 48.114  on 35  degrees of freedom
#> AIC: 50.114
#> 
#> Number of Fisher Scoring iterations: 4

Zu beachten ist, dass Logitwerte zurückgegeben werden; diese müssen ggf. noch in Wahrscheinlichkeiten rückgerechnet werden.

exp(coef(glm1))
#> (Intercept) 
#>   0.6363636

logit2prob <- function(logit){
  odds <- exp(logit)
  prob <- odds / (1 + odds)
  return(prob)
}

logit2prob(coef(glm1))
#> (Intercept) 
#>   0.3888889

Etwas komfortabler vielleicht geht es mit predict:

predict(glm1, type = "response", 
        newdata = NULL)
#>         1         2         3         4         5         6         7         8 
#> 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 
#>         9        10        11        12        13        14        15        16 
#> 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 
#>        17        18        19        20        21        22        23        24 
#> 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 
#>        25        26        27        28        29        30        31        32 
#> 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 
#>        33        34        35        36 
#> 0.3888889 0.3888889 0.3888889 0.3888889

Allerdings bezieht sich der p-Wert hier auf eine Referenz-Wahrscheinlchkeit von \(p_0 = 1/2\), so dass der p-Wert nicht vergleichbar ist mit den obigen Analysen.

5 Bayes-Test mit gleichverteilter Priorverteilung und MCMC-Sampler

glm2 <- stan_glm(success ~ 1, 
            data = d,
            prior = NULL,
            refresh = 0,
            family = "binomial")
glm2 %>% print()
#> stan_glm
#>  family:       binomial [logit]
#>  formula:      success ~ 1
#>  observations: 36
#>  predictors:   1
#> ------
#>             Median MAD_SD
#> (Intercept) -0.4    0.4  
#> 
#> ------
#> * For help interpreting the printed output see ?print.stanreg
#> * For info on the priors used see ?prior_summary.stanreg

Auch hier bekommen wir einen Logit zurück, den wir ggf. in eine Wahrscheinlichkeit umrechnen wollen:

coef(glm2)
#> (Intercept) 
#>  -0.4339619

logit2prob(coef(glm2))
#> (Intercept) 
#>   0.3931807

5.1 Zwischen-Fazit

Da finden sich doch ein paar Abweichungen im p-Wert; die Tests testen nicht (ganz) das Gleiche. Möglich, dass die Voraussetzungen jeweils nicht (ausreichend) erfüllt sind. Bei simulationsbasierten Verfahren kommt natürlich noch die Stichproben-Varianz hinzu, die für Ungewissheit im Schätzer sorgt.

6 Konfidenz-Intervall

6.1 Simulationsbasierte Inferenz (SBI)

set.seed(1896)
Bootvtlg <- do(1e4) * prop( ~success, 
                            data = resample(d), 
                            success = 1)
glimpse(Bootvtlg)
#> Rows: 10,000
#> Columns: 1
#> $ prop_1 <dbl> 0.4166667, 0.3333333, 0.5277778, 0.3611111, 0.4444444, 0.388888…

Die SD der Bootverteilung beträgt:

sd_boot <- sd(Bootvtlg$prop_1)
sd_boot
#> [1] 0.08153576

ggplot(Bootvtlg) +
  aes(x = prop_1) +
  geom_bar()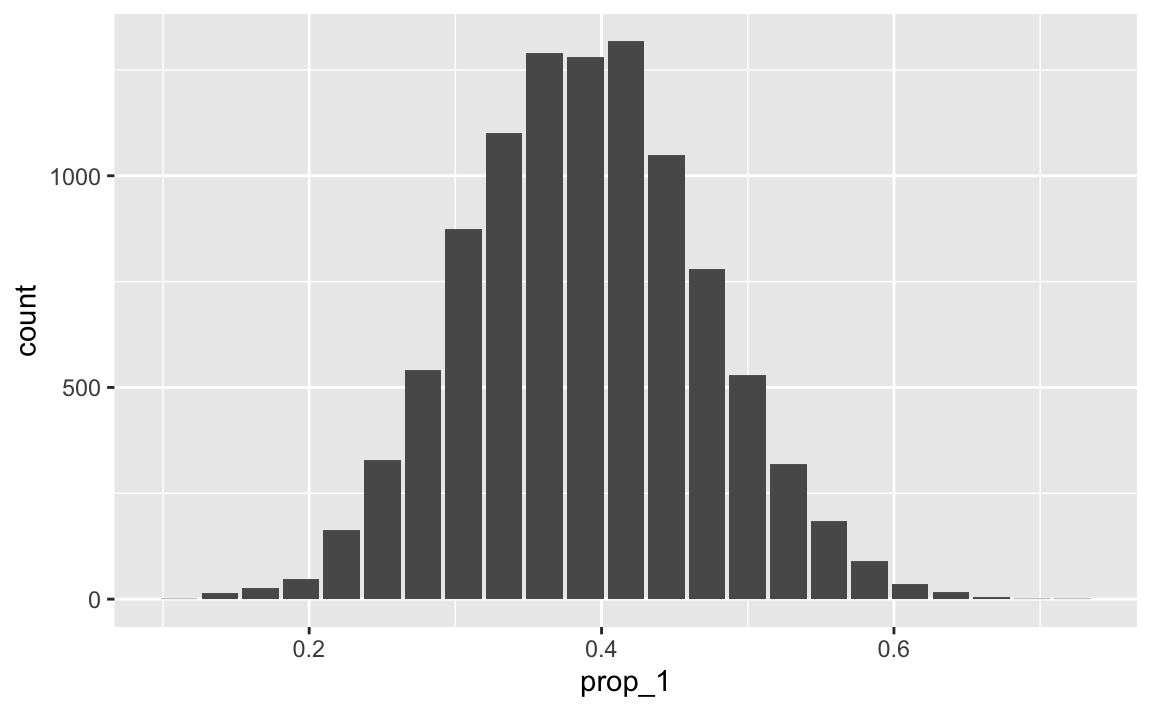

Wie man sieht, ist die Verteilung (annähernd) normalverteilt. D.h. man kann die Das Konfidenzintervall über die Näherung der Normalverteilungsquantile berechnen (s.u.).

KI-Grenzen:

ci95 <- quantile( ~ prop_1, data = Bootvtlg, probs = c(0.025, 0.975))

ci95
#>      2.5%     97.5% 
#> 0.2222222 0.5555556

Multipliziert man diese Anteilswerte mit \(n\), so bekommt man:

ci95[1]*n
#> 2.5% 
#>    8
ci95[2]*n
#> 97.5% 
#>    20

Anders gesagt liegen die Intervallgrenzen bei 8 und 20.

6.2 \(\chi^2\)-Test

Mit dem \(chi^2\)-Test kann man kein Konfidenzintervall für den Anteil bekommen, da die Prüfgröße nicht der Anteil ist.

6.2.1 Chi Square Bootstrap

Man könnte höchstens, wenn man unbedingt will, Die \(\chi^2\)-Prüfgröße bootstrappen…

Also los:

chi_boot <- do(10000) * {chisq.test(x = table(resample(d$success)),
                                  p = success_prob
) %>% extract2("statistic")}

glimpse(chi_boot)
#> Rows: 10,000
#> Columns: 1
#> $ X.squared <dbl> 1.250000e-01, 1.250000e-01, 1.125000e+00, 5.000000e-01, 1.25…

ggplot(chi_boot, aes(x = X.squared)) +
  geom_histogram(bins = 20)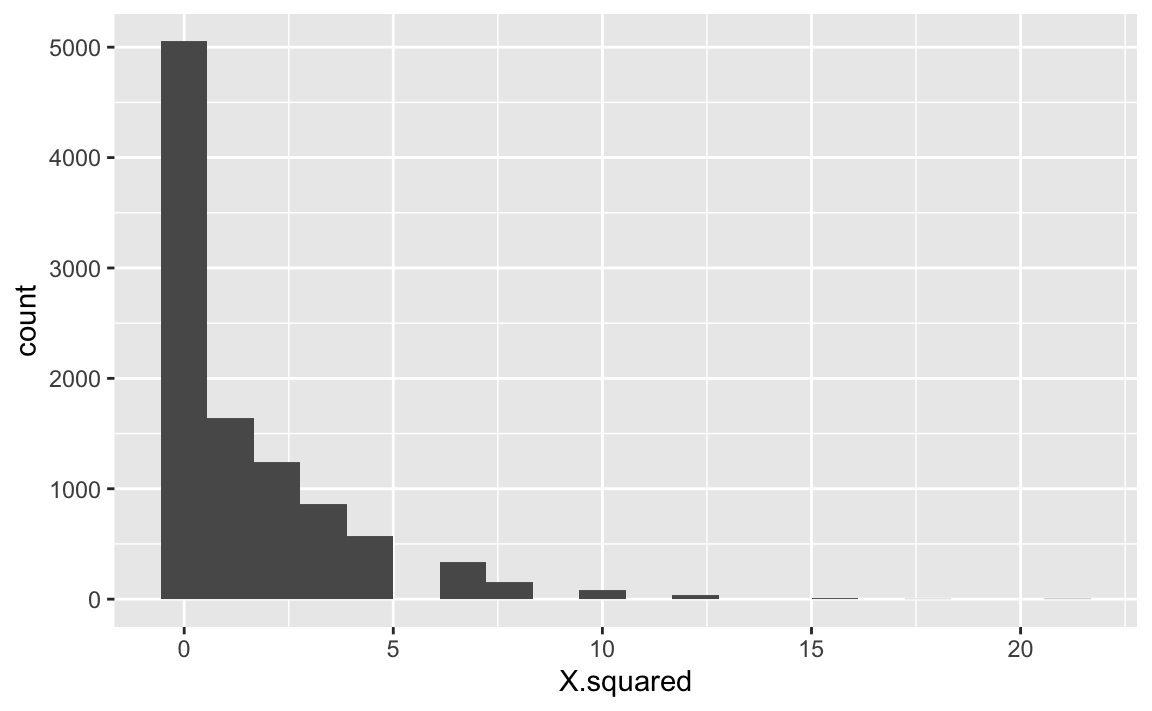

6.2.2 Chi p-value Bootstrap

In gleicher Manier kann man den p-Wert als Zufallsvariable auffassen und bootstrappen:

chi_p_boot <- do(10000) * {chisq.test(x = table(resample(d$success)),
                                  p = success_prob
) %>% extract2("p.value")}

glimpse(chi_p_boot)
#> Rows: 10,000
#> Columns: 1
#> $ result <dbl> 1.00000000, 0.15729921, 0.72367361, 0.47950012, 0.28884437, 0.4…

ggplot(chi_p_boot, aes(x = result)) +
  geom_histogram()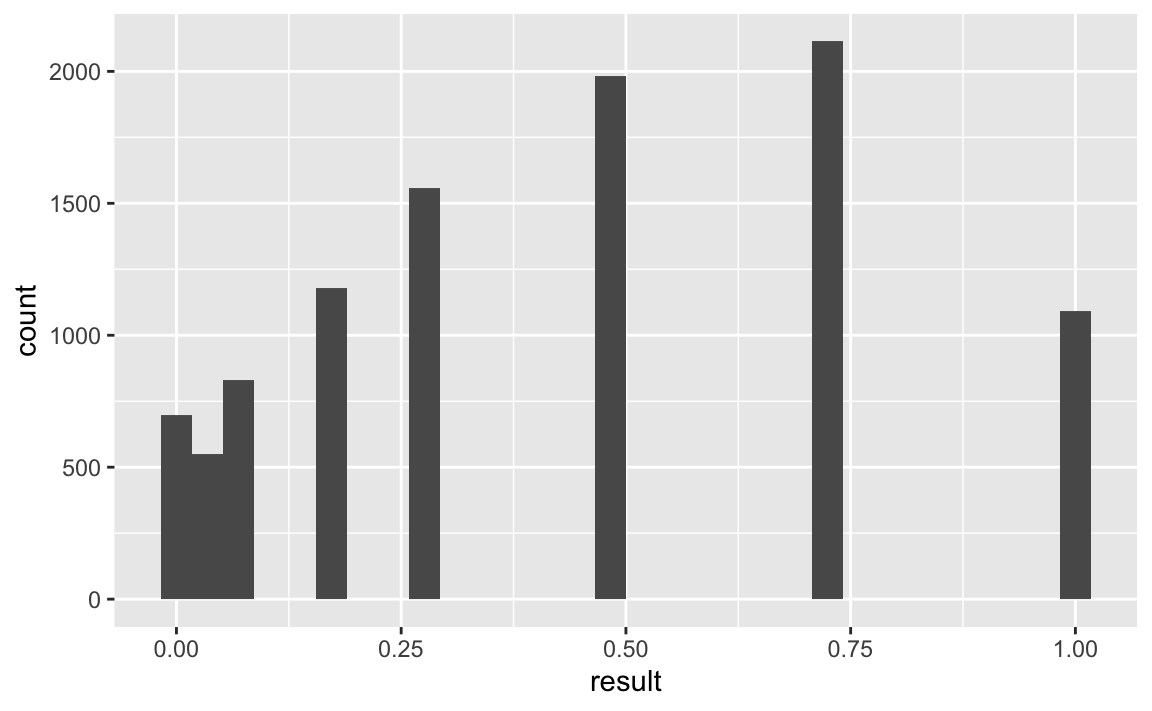

6.3 Binomial-Test, Näherung über Normalverteilung

Wie in der SBI gesehen, ist die Stichprobenverteilung bzw. die Bootstrapverteilung annähernd normalverteilt und zwar mit folgenden Parametern:

mue_boot <- x
sigma_boot <- sqrt(Var_X)

Dieser theoretische Wert entspricht gut dem durch die Simulation gefundenen Wert:

sd_boot*n
#> [1] 2.935288

6.4 Logistische Regression

Das kann man so machen (Quelle):

ci_glm1 <- predict(glm1, type = "response", se.fit = TRUE)
ci_glm1
#> $fit
#>         1         2         3         4         5         6         7         8 
#> 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 
#>         9        10        11        12        13        14        15        16 
#> 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 
#>        17        18        19        20        21        22        23        24 
#> 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 
#>        25        26        27        28        29        30        31        32 
#> 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 0.3888889 
#>        33        34        35        36 
#> 0.3888889 0.3888889 0.3888889 0.3888889 
#> 
#> $se.fit
#>          1          2          3          4          5          6          7 
#> 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 
#>          8          9         10         11         12         13         14 
#> 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 
#>         15         16         17         18         19         20         21 
#> 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 
#>         22         23         24         25         26         27         28 
#> 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 
#>         29         30         31         32         33         34         35 
#> 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 0.08124967 
#>         36 
#> 0.08124967 
#> 
#> $residual.scale
#> [1] 1

Da wir keinen Prädiktor haben, wird für alle Fälle der gleiche Wert vorhergesagt.

Nun “bauen” wir das KI basierend auf der Annahme einer Normalverteilung:

critval <- 1.96 ## approx 95% CI
upr <- ci_glm1$fit + (critval * ci_glm1$se.fit)
lwr <- ci_glm1$fit - (critval * ci_glm1$se.fit)

lwr[1]
#>         1 
#> 0.2296395
upr[1]
#>         1 
#> 0.5481382

Das sind die Anteilswerte; multiplizieren wir diese mit \(n\):

lwr[1]*n
#>        1 
#> 8.267023
upr[1]*n
#>        1 
#> 19.73298

Also liegen die Intervallgrenzen etwa bei 8 (unten) bzw. 19.7329767 (oben).

6.5 Zwischen-Fazit

Die Werte der Konfidenzintervall-Grenzen sind ziemlich ähnlich; das überrascht nicht, denn die Bootverteilung ist schön normalverteilt; die Binomialmethode basiert ebenfalls auf einer Approximation der Normalverteilung. Daher resultieren hier ähnliche Werte.

7 Fazit

Die Bootstrap-Methode funktioniert hier gut; natürlich hat sie auch hier Fallstricke.

Der p-Wert unterscheidet sich je Methode, weil die Signifikanztests unterschiedliche Prüfgrößen berechnen, sprich verschiedene Dinge berechnen.

8 Reproducibility

#> ─ Session info ───────────────────────────────────────────────────────────────────────────────────────────────────────
#>  setting  value                       
#>  version  R version 4.1.0 (2021-05-18)
#>  os       macOS Big Sur 10.16         
#>  system   x86_64, darwin17.0          
#>  ui       X11                         
#>  language (EN)                        
#>  collate  en_US.UTF-8                 
#>  ctype    en_US.UTF-8                 
#>  tz       Europe/Berlin               
#>  date     2021-07-29                  
#> 
#> ─ Packages ───────────────────────────────────────────────────────────────────────────────────────────────────────────
#>  package     * version  date       lib source                        
#>  assertthat    0.2.1    2019-03-21 [1] CRAN (R 4.1.0)                
#>  backports     1.2.1    2020-12-09 [1] CRAN (R 4.1.0)                
#>  blogdown      1.4      2021-07-23 [2] CRAN (R 4.1.0)                
#>  bookdown      0.22     2021-04-22 [2] CRAN (R 4.1.0)                
#>  broom         0.7.6    2021-04-05 [1] CRAN (R 4.1.0)                
#>  bslib         0.2.5.1  2021-05-18 [1] CRAN (R 4.1.0)                
#>  cellranger    1.1.0    2016-07-27 [1] CRAN (R 4.1.0)                
#>  cli           3.0.1    2021-07-17 [1] CRAN (R 4.1.0)                
#>  codetools     0.2-18   2020-11-04 [2] CRAN (R 4.1.0)                
#>  colorspace    2.0-2    2021-06-24 [1] CRAN (R 4.1.0)                
#>  crayon        1.4.1    2021-02-08 [1] CRAN (R 4.1.0)                
#>  crosstalk     1.1.1    2021-01-12 [2] CRAN (R 4.1.0)                
#>  DBI           1.1.1    2021-01-15 [1] CRAN (R 4.1.0)                
#>  dbplyr        2.1.1    2021-04-06 [1] CRAN (R 4.1.0)                
#>  digest        0.6.27   2020-10-24 [1] CRAN (R 4.1.0)                
#>  dplyr       * 1.0.7    2021-06-18 [1] CRAN (R 4.1.0)                
#>  ellipsis      0.3.2    2021-04-29 [1] CRAN (R 4.1.0)                
#>  evaluate      0.14     2019-05-28 [1] CRAN (R 4.1.0)                
#>  fansi         0.5.0    2021-05-25 [1] CRAN (R 4.1.0)                
#>  farver        2.1.0    2021-02-28 [1] CRAN (R 4.1.0)                
#>  forcats     * 0.5.1    2021-01-27 [1] CRAN (R 4.1.0)                
#>  fs            1.5.0    2020-07-31 [1] CRAN (R 4.1.0)                
#>  generics      0.1.0    2020-10-31 [1] CRAN (R 4.1.0)                
#>  ggdendro      0.1.22   2020-09-13 [1] CRAN (R 4.1.0)                
#>  ggforce       0.3.3    2021-03-05 [1] CRAN (R 4.1.0)                
#>  ggformula   * 0.10.1   2021-01-13 [1] CRAN (R 4.1.0)                
#>  ggplot2     * 3.3.5    2021-06-25 [1] CRAN (R 4.1.0)                
#>  ggrepel       0.9.1    2021-01-15 [2] CRAN (R 4.1.0)                
#>  ggridges    * 0.5.3    2021-01-08 [1] CRAN (R 4.1.0)                
#>  ggstance    * 0.3.5    2020-12-17 [1] CRAN (R 4.1.0)                
#>  glue          1.4.2    2020-08-27 [1] CRAN (R 4.1.0)                
#>  gridExtra     2.3      2017-09-09 [2] CRAN (R 4.1.0)                
#>  gtable        0.3.0    2019-03-25 [1] CRAN (R 4.1.0)                
#>  haven         2.4.1    2021-04-23 [1] CRAN (R 4.1.0)                
#>  hms           1.1.0    2021-05-17 [1] CRAN (R 4.1.0)                
#>  htmltools     0.5.1.1  2021-01-22 [1] CRAN (R 4.1.0)                
#>  htmlwidgets   1.5.3    2020-12-10 [2] CRAN (R 4.1.0)                
#>  httr          1.4.2    2020-07-20 [1] CRAN (R 4.1.0)                
#>  jquerylib     0.1.4    2021-04-26 [1] CRAN (R 4.1.0)                
#>  jsonlite      1.7.2    2020-12-09 [1] CRAN (R 4.1.0)                
#>  knitr         1.33     2021-04-24 [1] CRAN (R 4.1.0)                
#>  labelled      2.8.0    2021-03-08 [2] CRAN (R 4.1.0)                
#>  lattice     * 0.20-44  2021-05-02 [2] CRAN (R 4.1.0)                
#>  leaflet       2.0.4.1  2021-01-07 [1] CRAN (R 4.1.0)                
#>  lifecycle     1.0.0    2021-02-15 [1] CRAN (R 4.1.0)                
#>  lubridate     1.7.10   2021-02-26 [1] CRAN (R 4.1.0)                
#>  magrittr    * 2.0.1    2020-11-17 [1] CRAN (R 4.1.0)                
#>  MASS          7.3-54   2021-05-03 [2] CRAN (R 4.1.0)                
#>  Matrix      * 1.3-4    2021-06-01 [2] CRAN (R 4.1.0)                
#>  modelr        0.1.8    2020-05-19 [1] CRAN (R 4.1.0)                
#>  mosaic      * 1.8.3    2021-01-18 [1] CRAN (R 4.1.0)                
#>  mosaicCore    0.9.0    2021-01-16 [1] CRAN (R 4.1.0)                
#>  mosaicData  * 0.20.2   2021-01-16 [1] CRAN (R 4.1.0)                
#>  munsell       0.5.0    2018-06-12 [1] CRAN (R 4.1.0)                
#>  pillar        1.6.1    2021-05-16 [1] CRAN (R 4.1.0)                
#>  pkgconfig     2.0.3    2019-09-22 [1] CRAN (R 4.1.0)                
#>  plyr          1.8.6    2020-03-03 [1] CRAN (R 4.1.0)                
#>  polyclip      1.10-0   2019-03-14 [1] CRAN (R 4.1.0)                
#>  purrr       * 0.3.4    2020-04-17 [1] CRAN (R 4.1.0)                
#>  R6            2.5.0    2020-10-28 [1] CRAN (R 4.1.0)                
#>  Rcpp          1.0.7    2021-07-07 [1] CRAN (R 4.1.0)                
#>  readr       * 1.4.0    2020-10-05 [1] CRAN (R 4.1.0)                
#>  readxl        1.3.1    2019-03-13 [1] CRAN (R 4.1.0)                
#>  reprex        2.0.0    2021-04-02 [1] CRAN (R 4.1.0)                
#>  rlang         0.4.11   2021-04-30 [1] CRAN (R 4.1.0)                
#>  rmarkdown     2.9      2021-06-15 [1] CRAN (R 4.1.0)                
#>  rstudioapi    0.13     2020-11-12 [1] CRAN (R 4.1.0)                
#>  rvest         1.0.0    2021-03-09 [1] CRAN (R 4.1.0)                
#>  sass          0.4.0    2021-05-12 [1] CRAN (R 4.1.0)                
#>  scales      * 1.1.1    2020-05-11 [1] CRAN (R 4.1.0)                
#>  sessioninfo * 1.1.1    2018-11-05 [2] CRAN (R 4.1.0)                
#>  stringi       1.7.3    2021-07-16 [1] CRAN (R 4.1.0)                
#>  stringr     * 1.4.0    2019-02-10 [1] CRAN (R 4.1.0)                
#>  testthat    * 3.0.4    2021-07-01 [2] CRAN (R 4.1.0)                
#>  tibble      * 3.1.2    2021-05-16 [1] CRAN (R 4.1.0)                
#>  tidyr       * 1.1.3    2021-03-03 [1] CRAN (R 4.1.0)                
#>  tidyselect    1.1.1    2021-04-30 [1] CRAN (R 4.1.0)                
#>  tidyverse   * 1.3.1    2021-04-15 [1] CRAN (R 4.1.0)                
#>  tweenr        1.0.2    2021-03-23 [1] CRAN (R 4.1.0)                
#>  utf8          1.2.1    2021-03-12 [1] CRAN (R 4.1.0)                
#>  vctrs         0.3.8    2021-04-29 [1] CRAN (R 4.1.0)                
#>  withr         2.4.2    2021-04-18 [1] CRAN (R 4.1.0)                
#>  xfun          0.24     2021-06-15 [1] CRAN (R 4.1.0)                
#>  xml2          1.3.2    2020-04-23 [1] CRAN (R 4.1.0)                
#>  yaml          2.2.1.99 2021-06-18 [1] Github (viking/r-yaml@4788abe)
#> 
#> [1] /Users/sebastiansaueruser/Library/R/x86_64/4.1/library
#> [2] /Library/Frameworks/R.framework/Versions/4.1/Resources/library

Vergleich verschiedener Signifikanztstests bei einem Datensatz