1 Vorbereitung

library(tidyverse)
library(arm)

2 Ein unschuldiger Datensatz

Gehen wir davon aus, uns ist ein Datensatz gegeben. Die Hintergründe der Entstehung verlieren sich im Dunkel. Ich habe hier einen Datensatz simuliert; diese Details können Sie getrost überspringen. Nehmen Sie den Datensatz einfach als gegeben hin.

euler_e <- 2.71

d2 <- 
  tibble(
    x = rep(0:100, 10),
    y_hat = euler_e^(0.1*x) %>% round(2),
    e = rnorm(n = (101)*10) %>% round(2),
    y = y_hat + e
  )

glimpse(d2)

## Rows: 1,010
## Columns: 4
## $ x     <int> 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18…
## $ y_hat <dbl> 1.00, 1.10, 1.22, 1.35, 1.49, 1.65, 1.82, 2.01, 2.22, 2.45, 2.71…
## $ e     <dbl> -1.79, -0.31, 2.09, 0.58, -0.07, 0.35, -0.21, 0.60, -1.13, 0.48,…
## $ y     <dbl> -0.79, 0.79, 3.31, 1.93, 1.42, 2.00, 1.61, 2.61, 1.09, 2.93, 3.3…

y_hat ist der “wahre” Wert von Y, aber für uns unzugänglich. y ist der mit etwas Rauschen überlagerte echte Wert und der Wert, den wir messen.

3 lm1: additiv

Versuchen wir ein normales (“additives”) Modell klassischer Bauart.

lm1 <- lm(y ~ x, data = d2)

display(lm1)

## lm(formula = y ~ x, data = d2)
##             coef.est coef.se 
## (Intercept) -3076.92   202.21
## x             106.12     3.49
## ---
## n = 1010, k = 2
## residual sd = 3237.04, R-Squared = 0.48

Visualisierung:

ggplot(d2) +
  aes(x = x, y = y) +
  geom_point() +
  geom_smooth(method = "lm")

## `geom_smooth()` using formula 'y ~ x'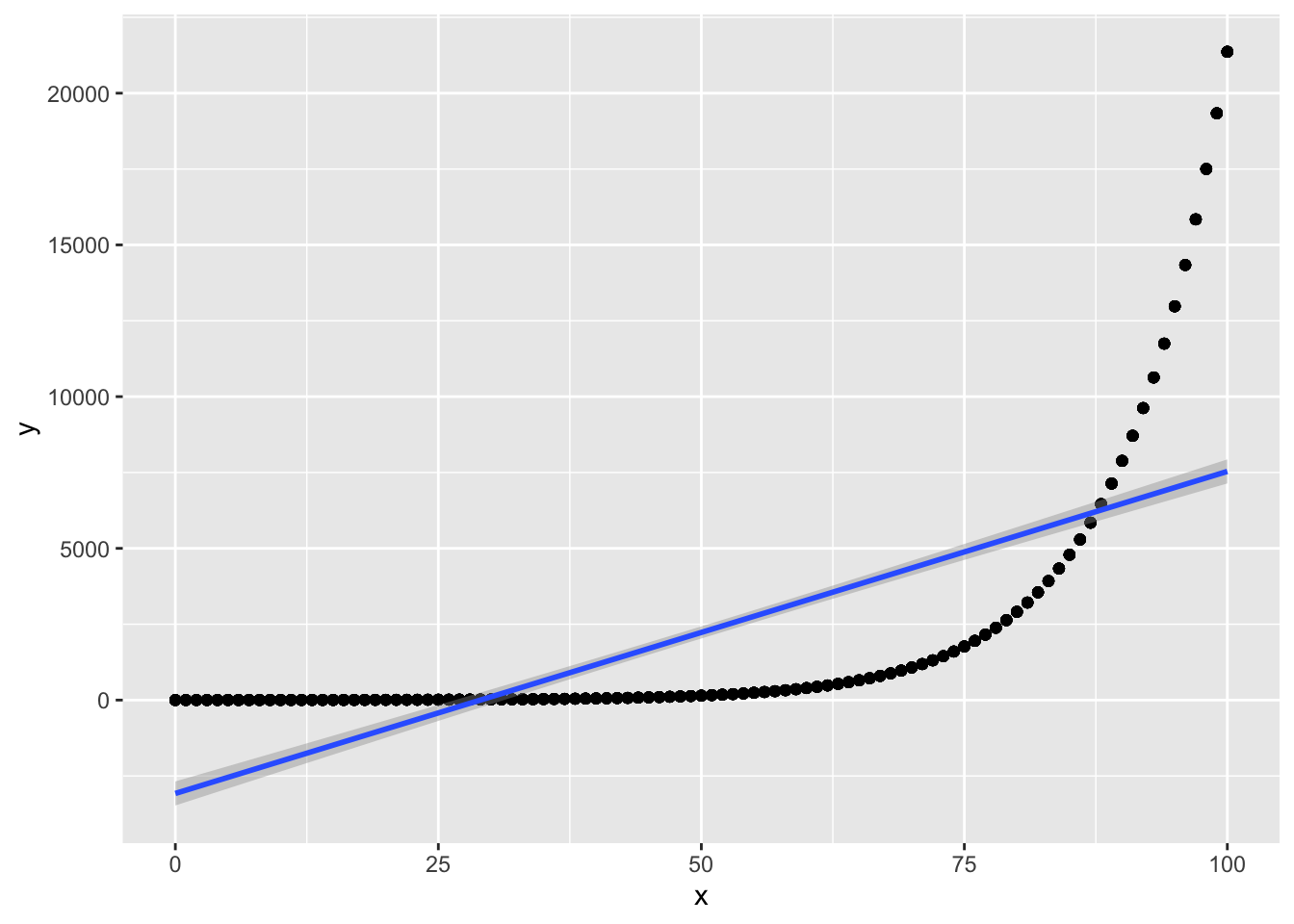

Passt irgendwie nicht so gut, die Regressionsgerade …

4 lm2: multiplikativ (exponenziell)

Jetzt probieren wir ein LogY-Modell; wir logarithmieren dazu die Y-Variable (die Basis des Logarithmus ist im Prinzip egal, ich empfehle aber e, weil oft am einfachsten zu interpretieren).

d3 <- 
  d2 %>% 
  filter(y > 0) %>% 
  mutate(y_log = log(y))

lm2 <- lm(y_log ~ x, data = d3)

display(lm2)

## lm(formula = y_log ~ x, data = d3)
##             coef.est coef.se
## (Intercept) -0.03     0.02  
## x            0.10     0.00  
## ---
## n = 1004, k = 2
## residual sd = 0.24, R-Squared = 0.99

ggplot(d3) +
  aes(x = x, y = y_log) +
  geom_point() +
  geom_smooth(method = "lm")

## `geom_smooth()` using formula 'y ~ x'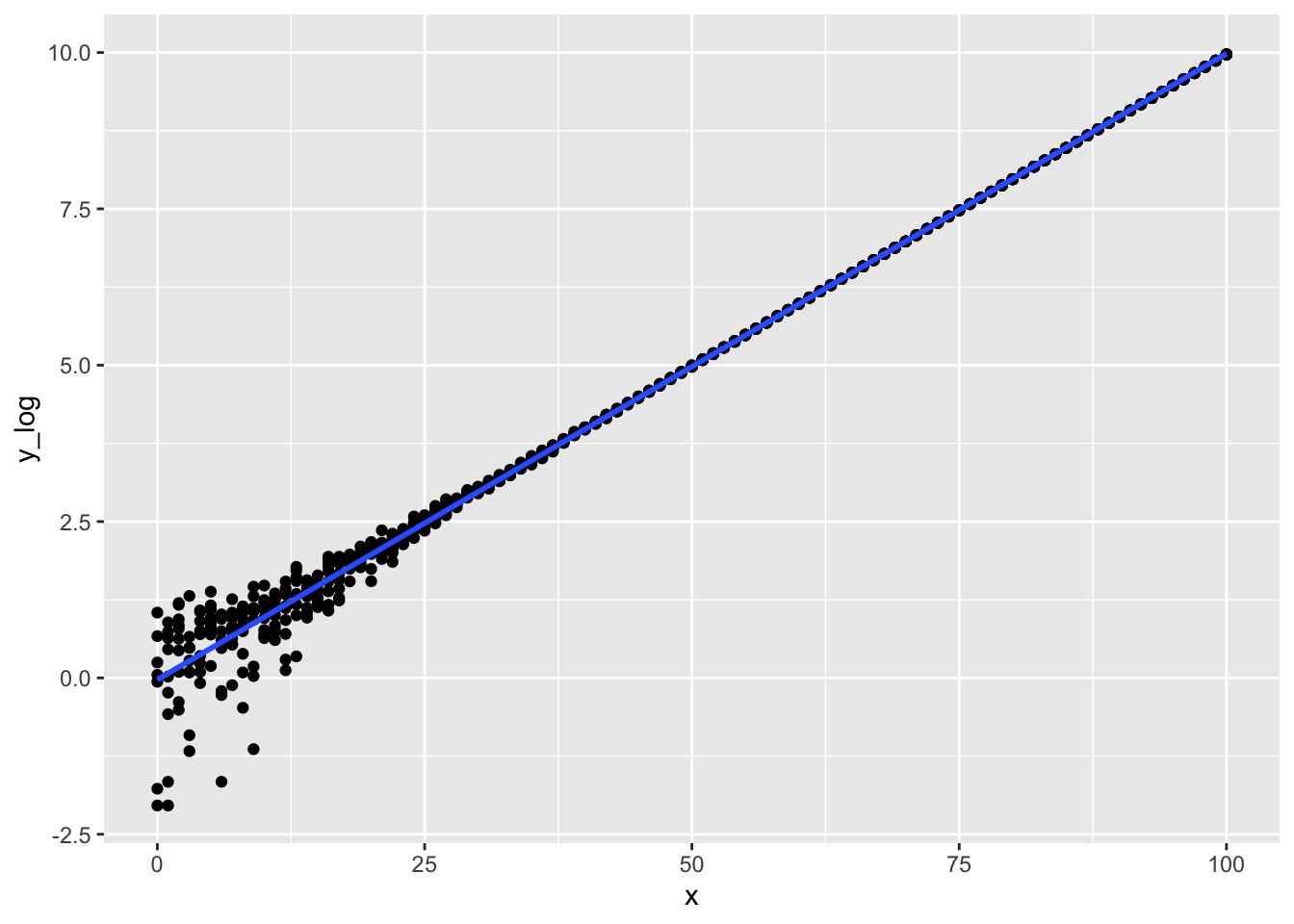

Passt. perfekt.

5 Fazit

👏YOU👏NEED👏THE👏LOG👏

Übrigens denkt unser Hirn in Logarithmen, s. hier (entspanntes, sofataugliches Video).

6 Take home message