3.1 z-Transformation des Prädiktors hp

mtcars <- 
  mtcars %>% 
  mutate(hp_z = scale(hp))

scale() besorgt die z-Transformation für uns, praktische Sache.

3.2 lm1

lm1 <- lm(mpg ~ hp + am + hp:am,
          data = mtcars)
display(lm1)

## lm(formula = mpg ~ hp + am + hp:am, data = mtcars)
##             coef.est coef.se
## (Intercept) 26.62     2.18  
## hp          -0.06     0.01  
## am           5.22     2.67  
## hp:am        0.00     0.02  
## ---
## n = 32, k = 4
## residual sd = 2.96, R-Squared = 0.78

Wie man in der Ausgabe sehen kann, gibt es keinen Interaktionseffekt: Der Koeffizient liegt im Modell bei 0.00 (se=0.02). Pustekuchen. Also suchen wir uns einen anderen Datensatz.

4.1 Daten

teacherratings <- read_csv("https://vincentarelbundock.github.io/Rdatasets/csv/AER/TeachingRatings.csv")

## Warning: Missing column names filled in: 'X1' [1]

## 
## ── Column specification ────────────────────────────────────────────────────────
## cols(
##   X1 = col_double(),
##   minority = col_character(),
##   age = col_double(),
##   gender = col_character(),
##   credits = col_character(),
##   beauty = col_double(),
##   eval = col_double(),
##   division = col_character(),
##   native = col_character(),
##   tenure = col_character(),
##   students = col_double(),
##   allstudents = col_double(),
##   prof = col_double()
## )

Eine Codebook findet sich hier.

4.2 Ohne z-Transformation

lm2 <- lm(eval ~ beauty + gender + beauty:gender,
          data = teacherratings)

display(lm2)

## lm(formula = eval ~ beauty + gender + beauty:gender, data = teacherratings)
##                   coef.est coef.se
## (Intercept)       3.89     0.04   
## beauty            0.09     0.05   
## gendermale        0.20     0.05   
## beauty:gendermale 0.11     0.06   
## ---
## n = 463, k = 4
## residual sd = 0.54, R-Squared = 0.07

4.3 Mit z-Transformation

teacherratings <-
  teacherratings %>% 
  mutate(beauty_z = (beauty - mean(beauty))/sd(beauty),
         age_z = (age - mean(age))/sd(age))

Dieses Mal haben wir die z-Transformation per Hand gerechnet.

lm3 <- lm(eval ~ age_z + gender + age_z:gender,
          data = teacherratings)

display(lm3)

## lm(formula = eval ~ age_z + gender + age_z:gender, data = teacherratings)
##                  coef.est coef.se
## (Intercept)       3.86     0.04  
## age_z            -0.13     0.04  
## gendermale        0.22     0.05  
## age_z:gendermale  0.11     0.06  
## ---
## n = 463, k = 4
## residual sd = 0.55, R-Squared = 0.04

4.4 Visualisierung

vis1 <- ggplot(teacherratings) +
  aes(x = age_z, y = eval, color = gender) +
  geom_point() +
  geom_smooth(method = "lm") +
  scale_color_brewer(palette="Set1")

vis1 

## `geom_smooth()` using formula 'y ~ x'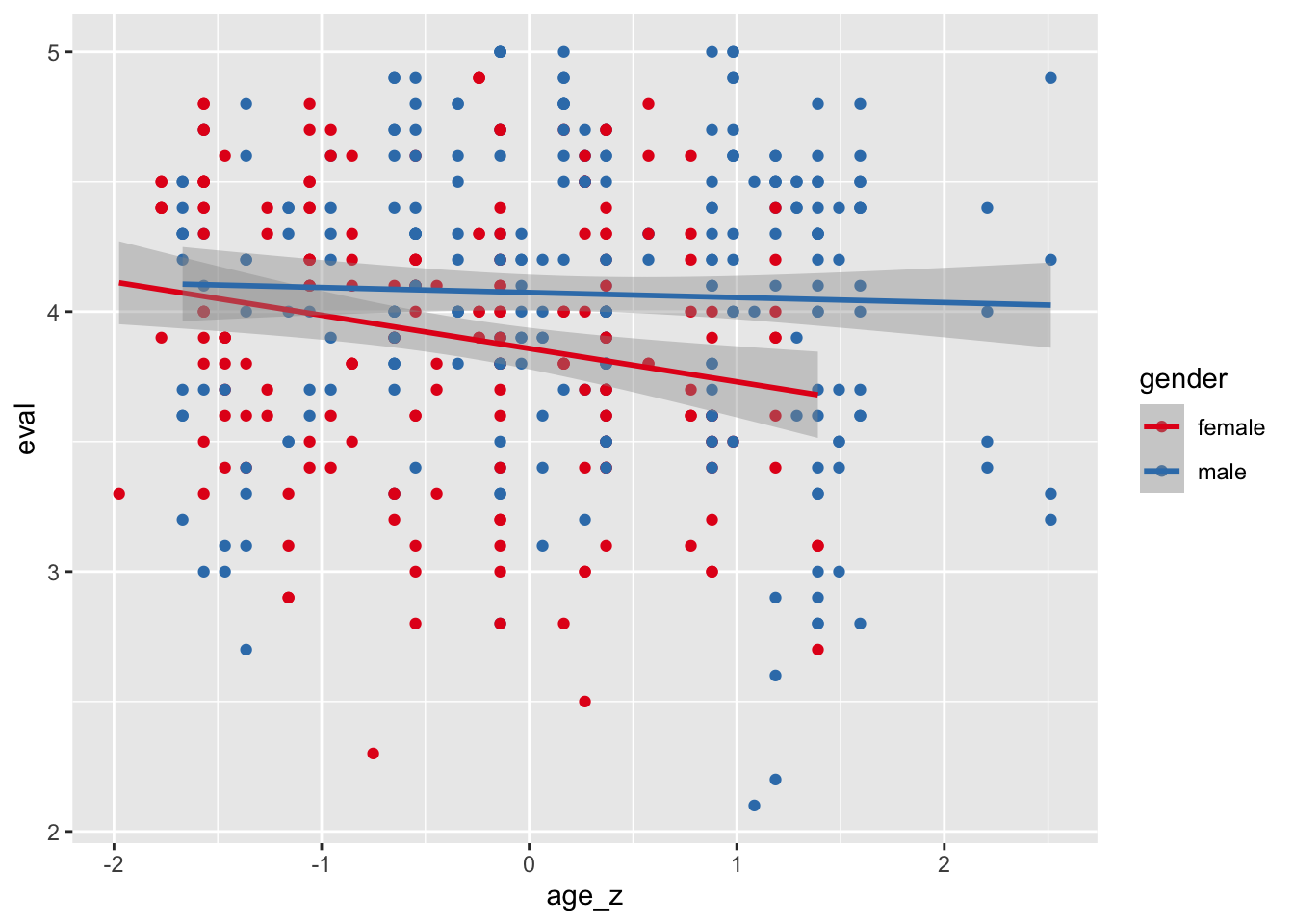

4.5 Interpretation zum Vorhandensein eines Interpretationseffekts

Da die Gerade nicht parallel sind, liegt ein Interaktionseffekt vor. Allerdings ist das Verhältnis von Signal zu Rauschen kleiner als 2, was als Beleg dafür gelten kann, dass auch ein Koeffizient von 0 (keine Interaktion) zu den Daten passen würde (mit den Daten kompatibel ist). Die gleiche Abwägung von Signal zu Rauschen ist bei den anderen Koeffizienten auch zu treffen.

4.6 Interpretation der Koeffizienten

• Intercept: Die mittlere Bewertung von weiblichen Dozenten mit mittlerem Alter liegt im Modell bei knapp 4.
• age_z: Pro Jahr an zusätzlichem Alter sinkt die Bewertung der Frauen um -0.13 Punkte (im Schnitt).
• gendermale: Die mittlere Bewertung von männlichen Dozenten mit mittlerem Alter liegt im Modell 0.22 Punkten über dem der Frauen, also bei 3.86+0.22, d.i. etwas über 4.
• age_z:gendermale: Für jedes Altersjahr steigt die mittlere Bewertung der männlichen Dozentis um 0.11 mehr als dies bei den Frauen der Fall ist, also um -0.13+0.11, d.i. etwa -0.02 Punkte.

4.7 Viel besser mit z-Transformation

Ohne z-Transformation wäre der “Bezugspunkt” immer 0 Jahre Alter, was für Dozentis nicht so das typische Berufsjahr ist… Mit z-Transformation ist der “Bezguspunkt” (der Nullwert) das mittlere Alter des Dozentis (in der Stichprobe). Viel schöner zu interpretieren!

4.8 Berechnen eines vorhergesagten Wertes mit der Hand

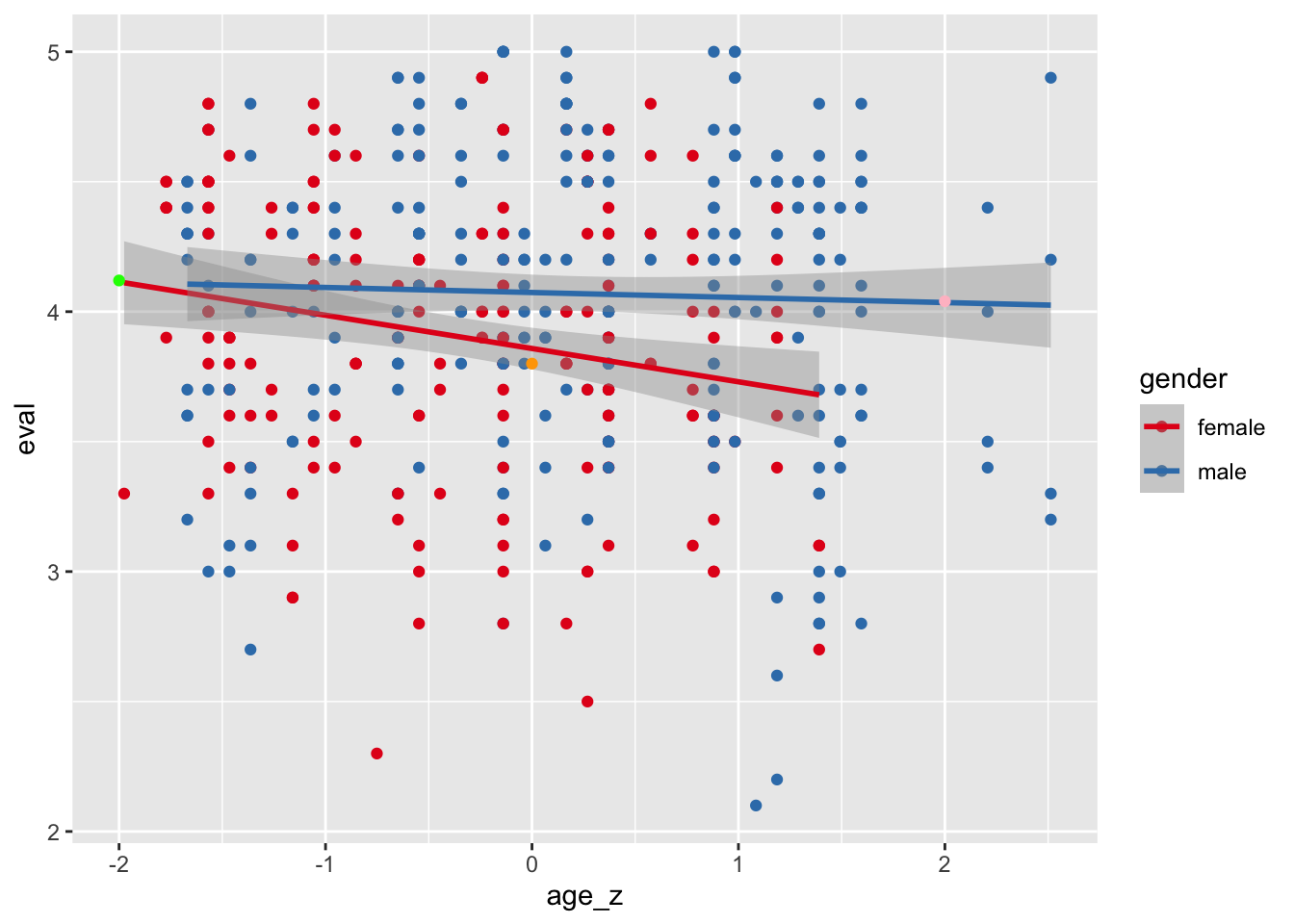
Was ist die zu erwartenden Bewertung von folgenden Dozentis:

• Dozi 1: Frau, mittlere Schönheit (Frau Orange)
• Dozi 2: Mann, Alter (z) = 2 (Herr Rosa)
• Dozi 3: Fau, Alter (z) = -2 (Frau Grün)

y1 <- 3.8 - 0.13*0 + 0*0.22 + 0.11*(0*0)
y2 <- 3.86 - 0.13*2 + 1*0.22 + 0.11*(1*2)
y3 <- 3.86 - 0.13*(-2) + 0*0.22 + 0.11*(0*-2)

vis1 +
  annotate(geom = "point", x = 0, y = y1, color = "orange") +
  annotate(geom = "point", x = 2, y = y2, color = "pink") +
  annotate(geom = "point", x = -2, y = y3, color = "green")

## `geom_smooth()` using formula 'y ~ x'