- 1 Setup
- 2 Forschungsfrage und Hintergrund
- 3 ACHTUNG
- 4 Daten laden
- 5 Aufgaben
- 6 Los geht’s
- 6.1 Geben Sie zentrale deskriptive Statistiken an für Affärenhäufigkeit und Ehezufriedenheit!
- 6.2 Visualisieren Sie zentrale Variablen!
- 6.3 Wer ist zufriedener mit der Partnerschaft: Personen mit Kindern oder ohne?
- 6.4 Wie viele fehlende Werte gibt es? Was machen wir am besten damit?
- 6.5 Wer ist glücklicher in der Partnerschaft: Männer oder Frauen?
- 6.6 Berechnen und visualisieren Sie zentrale Korrelationen!
- 6.7 Wie groß ist der (statistische) “Einfluss” (das Einflussgewicht) der Ehejahre bzw. Ehezufriedenheit auf die Anzahl der Affären?
- 6.8 Um wie viel erhöht sich die erklärte Varianz (R-Quadrat) von Affärenhäufigkeit wenn man den Prädiktor Ehezufriedenheit zum Prädiktor Ehejahre hinzufügt? (Wie) verändern sich die Einflussgewichte (b)?
- 6.9 Welche Prädiktoren würden Sie noch in die Regressionsanalyse aufnehmen?
- 6.10 Unterscheiden sich die Geschlechter (deutlich) in ihrer Zufriedenheit mit der Partnerschaft und in der Häufigkeit von Seitensprüngen? Wie groß ist der Unterschied?
- 6.11 Rechnen Sie die Regressionsanalyse getrennt für kinderlose Ehe und Ehen mit Kindern!
- 6.12 Rechnen Sie die Regression nur für “Halodries”; d.h. für Menschen mit Seitensprüngen. Dafür müssen Sie alle Menschen ohne Affären aus den Datensatz entfernen.
1 Setup
library(tidyverse)
library(skimr)
library(corrr)2 Forschungsfrage und Hintergrund
Wovon ist die Häufigkeit von Affären (Seitensprüngen) in Ehen abhängig (nur prädiktiv!)? Diese Frage soll anhand des Datensatzes Affair untersucht werden.
Dieser Post stellt beispielhaft eine grundlegende Methoden der praktischen Datenanalyse im Rahmen einer kleinen Fallstudie (YACSDA) vor.
3 ACHTUNG
In dieser Analyse wird (fälschlich!) davon ausgegangen, dass affairs die Anzahl der Affären angibt. Erst nach der Analyse habe ich erkannt, dass die Variable nur ordinal skaliert ist. Mehr Infos finden sich im Codebook.
4 Daten laden
Quelle der Daten: http://statsmodels.sourceforge.net/0.5.0/datasets/generated/fair.html
Der Datensatz findet sich (in ähnlicher Form) auch im R-Paket COUNT (https://cran.r-project.org/web/packages/COUNT/index.html).
Laden wir als erstes den Datensatz in R:
d <- read_csv("https://vincentarelbundock.github.io/Rdatasets/csv/AER/Affairs.csv")glimpse(d)
#> Rows: 601
#> Columns: 10
#> $ X1 <dbl> 4, 5, 11, 16, 23, 29, 44, 45, 47, 49, 50, 55, 64, 80, 86…
#> $ affairs <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
#> $ gender <chr> "male", "female", "female", "male", "male", "female", "f…
#> $ age <dbl> 37, 27, 32, 57, 22, 32, 22, 57, 32, 22, 37, 27, 47, 22, …
#> $ yearsmarried <dbl> 10.00, 4.00, 15.00, 15.00, 0.75, 1.50, 0.75, 15.00, 15.0…
#> $ children <chr> "no", "no", "yes", "yes", "no", "no", "no", "yes", "yes"…
#> $ religiousness <dbl> 3, 4, 1, 5, 2, 2, 2, 2, 4, 4, 2, 4, 5, 2, 4, 1, 2, 3, 2,…
#> $ education <dbl> 18, 14, 12, 18, 17, 17, 12, 14, 16, 14, 20, 18, 17, 17, …
#> $ occupation <dbl> 7, 6, 1, 6, 6, 5, 1, 4, 1, 4, 7, 6, 6, 5, 5, 5, 4, 5, 5,…
#> $ rating <dbl> 4, 4, 4, 5, 3, 5, 3, 4, 2, 5, 2, 4, 4, 4, 4, 5, 3, 4, 5,…5 Aufgaben
- Geben Sie zentrale deskriptive Statistiken an für Affärenhäufigkeit und Ehezufriedenheit!
- Visualisieren Sie zentrale Variablen!
- Wer ist zufriedener mit der Partnerschaft: Personen mit Kindern oder ohne?
- Wie viele fehlende Werte gibt es? Was machen wir am besten damit?
- Wer ist glücklicher in der Partnerschaft: Männer oder Frauen?
- Berechnen und visualisieren Sie zentrale Korrelationen!
- Wie groß ist der (statistische) Effekt (das Einflussgewicht) der Ehejahre bzw. Ehezufriedenheit auf die Anzahl der Affären?
- Um wie viel erhöht sich die erklärte Varianz (R-Quadrat) von Affärenhäufigkeit wenn man den Prädiktor Ehezufriedenheit zum Prädiktor Ehejahre hinzufügt? (Wie) verändern sich die Einflussgewichte (b)?
- Welche Prädiktoren würden Sie noch in die Regressionsanalyse aufnehmen?
- Unterscheiden sich die Geschlechter (deutlich) in ihrer Zufriedenheit mit der Partnerschaft und in der Häufigkeit von Seitensprüngen? Wie groß ist der Unterschied?
- Rechnen Sie die Regressionsanalyse getrennt für kinderlose Ehe und Ehen mit Kindern!
- Rechnen Sie die Regression nur für “Halodries”; d.h. für Menschen mit Seitensprüngen. Dafür müssen Sie alle Menschen ohne Affären aus den Datensatz entfernen.
6 Los geht’s
6.1 Geben Sie zentrale deskriptive Statistiken an für Affärenhäufigkeit und Ehezufriedenheit!
d %>%
summarise(rating_avg = mean(rating),
rating_sd = sd(rating))
#> # A tibble: 1 x 2
#> rating_avg rating_sd
#> <dbl> <dbl>
#> 1 3.93 1.10d %>%
skim()| Name | Piped data |
| Number of rows | 601 |
| Number of columns | 10 |
| _______________________ | |
| Column type frequency: | |
| character | 2 |
| numeric | 8 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| gender | 0 | 1 | 4 | 6 | 0 | 2 | 0 |
| children | 0 | 1 | 2 | 3 | 0 | 2 | 0 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| X1 | 0 | 1 | 1059.72 | 914.90 | 4.00 | 528 | 1009 | 1453 | 9029 | ▇▁▁▁▁ |
| affairs | 0 | 1 | 1.46 | 3.30 | 0.00 | 0 | 0 | 0 | 12 | ▇▁▁▁▁ |
| age | 0 | 1 | 32.49 | 9.29 | 17.50 | 27 | 32 | 37 | 57 | ▃▇▂▂▁ |
| yearsmarried | 0 | 1 | 8.18 | 5.57 | 0.12 | 4 | 7 | 15 | 15 | ▆▅▃▃▇ |
| religiousness | 0 | 1 | 3.12 | 1.17 | 1.00 | 2 | 3 | 4 | 5 | ▂▇▆▇▃ |
| education | 0 | 1 | 16.17 | 2.40 | 9.00 | 14 | 16 | 18 | 20 | ▁▂▆▇▇ |
| occupation | 0 | 1 | 4.19 | 1.82 | 1.00 | 3 | 5 | 6 | 7 | ▅▂▂▇▆ |
| rating | 0 | 1 | 3.93 | 1.10 | 1.00 | 3 | 4 | 5 | 5 | ▁▂▃▇▇ |
d %>%
count(affairs)
#> # A tibble: 6 x 2
#> affairs n
#> <dbl> <int>
#> 1 0 451
#> 2 1 34
#> 3 2 17
#> 4 3 19
#> 5 7 42
#> 6 12 386.2 Visualisieren Sie zentrale Variablen!
6.2.1 affairs
ggplot(d) +
aes(x = affairs) +
geom_bar()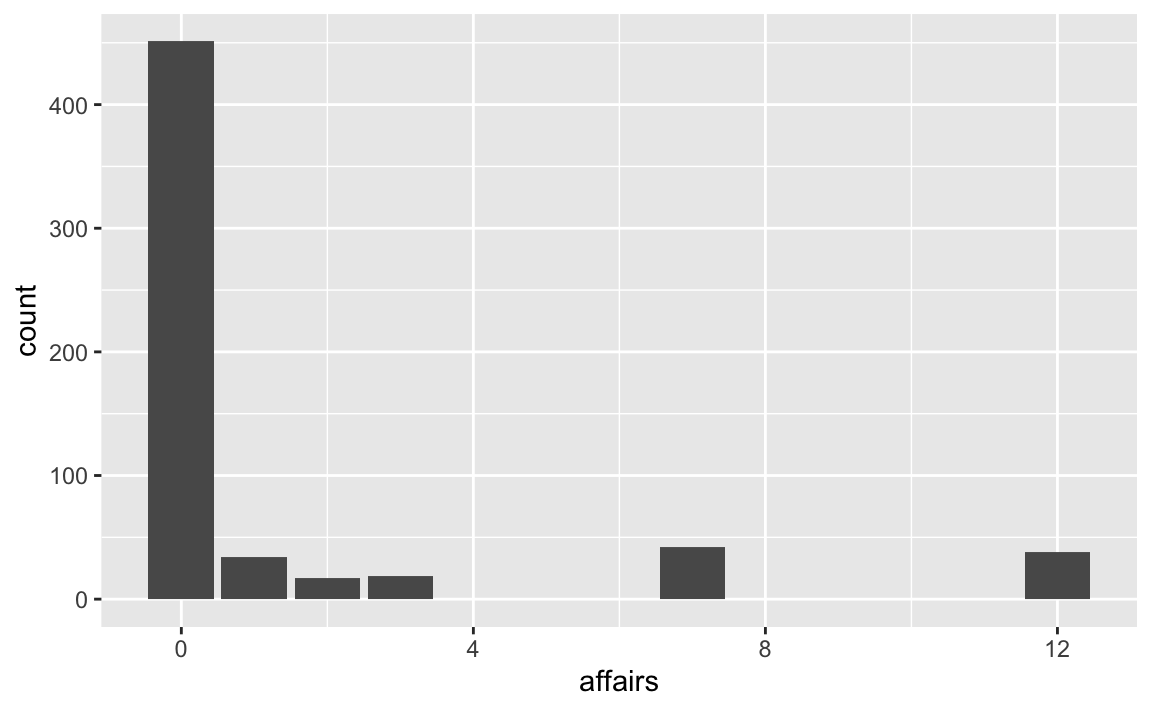
6.2.2 rating
ggplot(d) +
aes(x = rating) +
geom_histogram()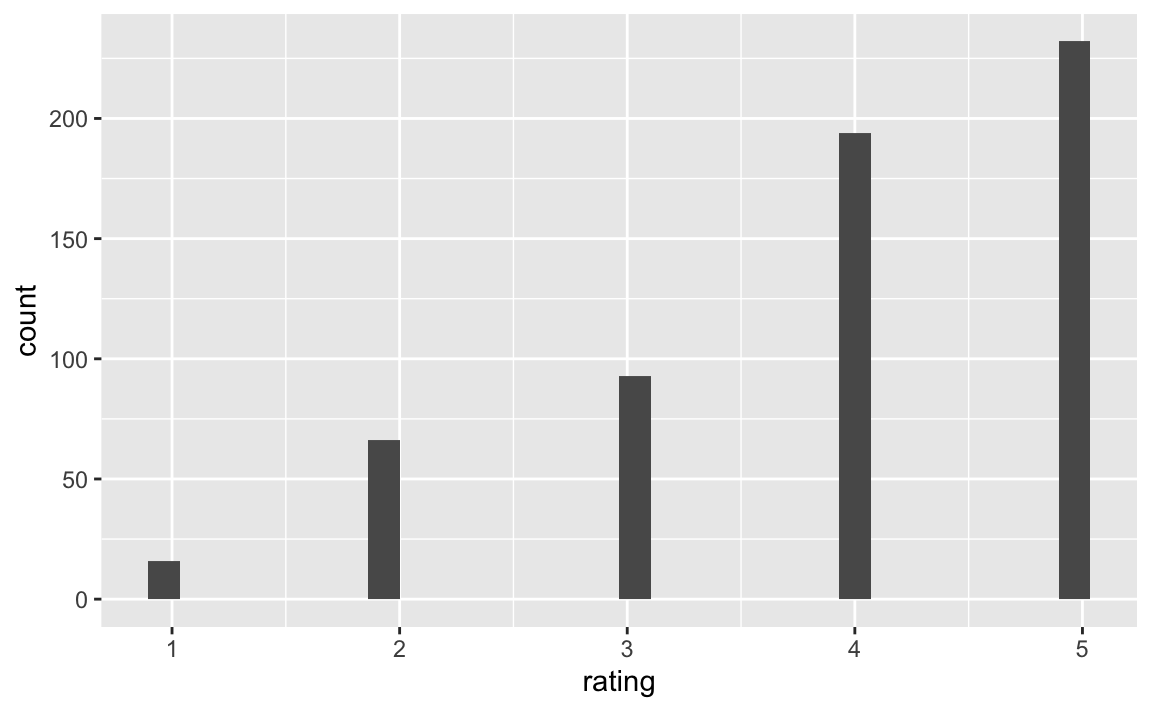
ggplot(d) +
aes(y = rating) +
geom_boxplot()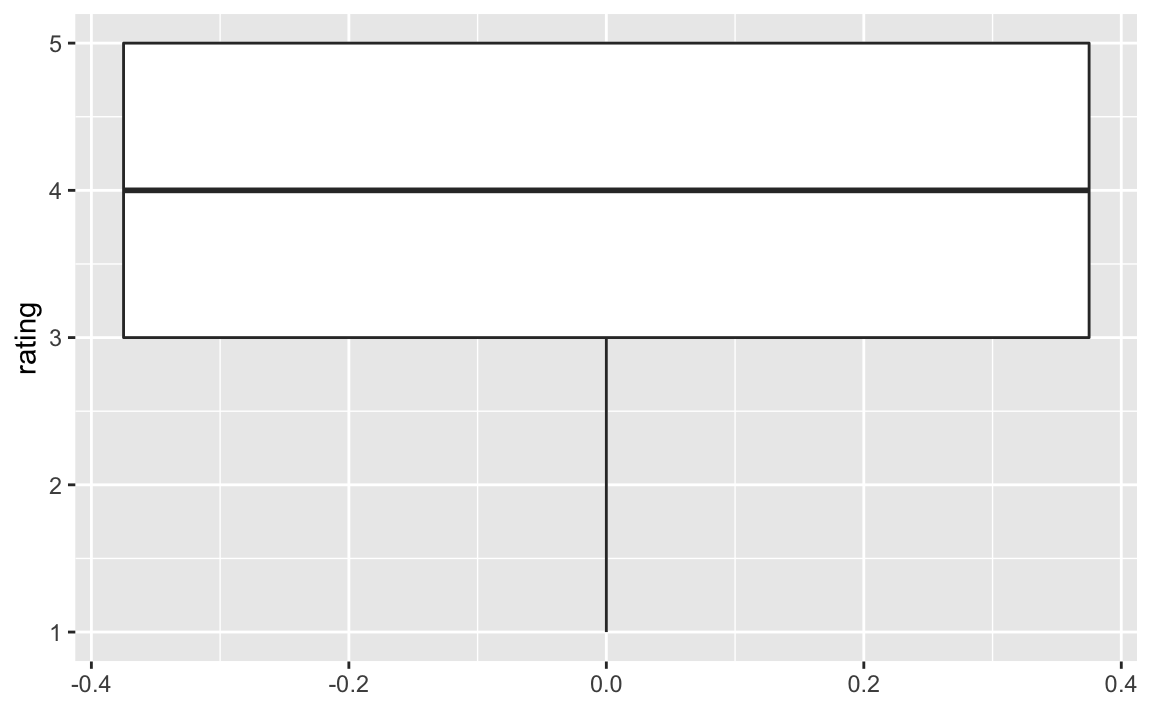
6.3 Wer ist zufriedener mit der Partnerschaft: Personen mit Kindern oder ohne?
d %>%
group_by(children) %>%
summarise(rating_avg = mean(rating))
#> # A tibble: 2 x 2
#> children rating_avg
#> <chr> <dbl>
#> 1 no 4.27
#> 2 yes 3.806.4 Wie viele fehlende Werte gibt es? Was machen wir am besten damit?
d %>%
filter(is.na(affairs))
#> # A tibble: 0 x 10
#> # … with 10 variables: X1 <dbl>, affairs <dbl>, gender <chr>, age <dbl>,
#> # yearsmarried <dbl>, children <chr>, religiousness <dbl>, education <dbl>,
#> # occupation <dbl>, rating <dbl>d %>%
drop_na()
#> # A tibble: 601 x 10
#> X1 affairs gender age yearsmarried children religiousness education
#> <dbl> <dbl> <chr> <dbl> <dbl> <chr> <dbl> <dbl>
#> 1 4 0 male 37 10 no 3 18
#> 2 5 0 female 27 4 no 4 14
#> 3 11 0 female 32 15 yes 1 12
#> 4 16 0 male 57 15 yes 5 18
#> 5 23 0 male 22 0.75 no 2 17
#> 6 29 0 female 32 1.5 no 2 17
#> 7 44 0 female 22 0.75 no 2 12
#> 8 45 0 male 57 15 yes 2 14
#> 9 47 0 female 32 15 yes 4 16
#> 10 49 0 male 22 1.5 no 4 14
#> # … with 591 more rows, and 2 more variables: occupation <dbl>, rating <dbl>d %>%
filter(if_any(everything(), ~ is.na(.)))
#> # A tibble: 0 x 10
#> # … with 10 variables: X1 <dbl>, affairs <dbl>, gender <chr>, age <dbl>,
#> # yearsmarried <dbl>, children <chr>, religiousness <dbl>, education <dbl>,
#> # occupation <dbl>, rating <dbl>6.5 Wer ist glücklicher in der Partnerschaft: Männer oder Frauen?
d %>%
group_by(gender) %>%
summarise(rating_avg = mean(rating))
#> # A tibble: 2 x 2
#> gender rating_avg
#> <chr> <dbl>
#> 1 female 3.94
#> 2 male 3.926.6 Berechnen und visualisieren Sie zentrale Korrelationen!
d %>%
summarise(cor1 = cor(rating, affairs))
#> # A tibble: 1 x 1
#> cor1
#> <dbl>
#> 1 -0.280d %>%
select(where(is.numeric)) %>%
correlate() %>%
focus(rating)
#> # A tibble: 7 x 2
#> term rating
#> <chr> <dbl>
#> 1 X1 -0.0144
#> 2 affairs -0.280
#> 3 age -0.199
#> 4 yearsmarried -0.243
#> 5 religiousness 0.0243
#> 6 education 0.109
#> 7 occupation 0.0174d %>%
select(where(is.numeric)) %>%
correlate() %>%
rplot()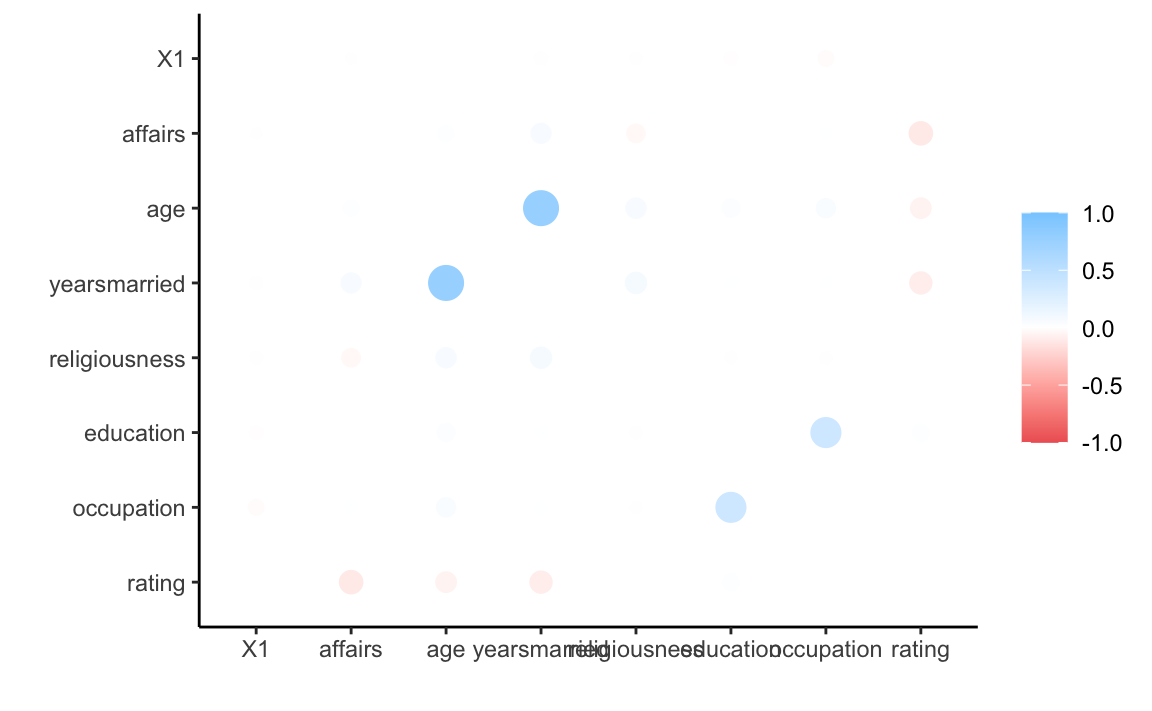
6.7 Wie groß ist der (statistische) “Einfluss” (das Einflussgewicht) der Ehejahre bzw. Ehezufriedenheit auf die Anzahl der Affären?
lm1 <- lm(affairs ~ yearsmarried + rating,
data = d)
summary(lm1)
#>
#> Call:
#> lm(formula = affairs ~ yearsmarried + rating, data = d)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.1474 -1.6495 -0.8365 -0.1616 11.8945
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.76913 0.56715 6.646 6.80e-11 ***
#> yearsmarried 0.07481 0.02377 3.147 0.00173 **
#> rating -0.74395 0.12005 -6.197 1.07e-09 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.147 on 598 degrees of freedom
#> Multiple R-squared: 0.09315, Adjusted R-squared: 0.09012
#> F-statistic: 30.71 on 2 and 598 DF, p-value: 2.01e-13d2 <-
d %>%
mutate(affairs_z = (affairs - mean(affairs)) / sd(affairs),
yearsmarried_z = scale(yearsmarried),
rating_z = scale(rating)) %>%
select(affairs, affairs_z, everything())lm2 <- lm(affairs ~ yearsmarried_z + rating_z,
data = d2)
summary(lm2)
#>
#> Call:
#> lm(formula = affairs ~ yearsmarried_z + rating_z, data = d2)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.1474 -1.6495 -0.8365 -0.1616 11.8945
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.4559 0.1284 11.343 < 2e-16 ***
#> yearsmarried_z 0.4168 0.1324 3.147 0.00173 **
#> rating_z -0.8207 0.1324 -6.197 1.07e-09 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.147 on 598 degrees of freedom
#> Multiple R-squared: 0.09315, Adjusted R-squared: 0.09012
#> F-statistic: 30.71 on 2 and 598 DF, p-value: 2.01e-136.8 Um wie viel erhöht sich die erklärte Varianz (R-Quadrat) von Affärenhäufigkeit wenn man den Prädiktor Ehezufriedenheit zum Prädiktor Ehejahre hinzufügt? (Wie) verändern sich die Einflussgewichte (b)?
lm1 <- lm(affairs ~ yearsmarried,
data = d)
summary(lm1)
#>
#> Call:
#> lm(formula = affairs ~ yearsmarried, data = d)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -2.2106 -1.6575 -0.9937 -0.5974 11.3658
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.55122 0.23511 2.345 0.0194 *
#> yearsmarried 0.11063 0.02377 4.655 4e-06 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.243 on 599 degrees of freedom
#> Multiple R-squared: 0.03491, Adjusted R-squared: 0.0333
#> F-statistic: 21.67 on 1 and 599 DF, p-value: 3.996e-066.9 Welche Prädiktoren würden Sie noch in die Regressionsanalyse aufnehmen?
Hm…
- Apriori-Wissen (Theorie der Ehezufriedenheit)
- Signal-Rausch-Verhältnisses (Estimate/SE)
- EDA
- …
6.10 Unterscheiden sich die Geschlechter (deutlich) in ihrer Zufriedenheit mit der Partnerschaft und in der Häufigkeit von Seitensprüngen? Wie groß ist der Unterschied?
nicht ausgeführt! p-Wert …
6.11 Rechnen Sie die Regressionsanalyse getrennt für kinderlose Ehe und Ehen mit Kindern!
lm3 <- lm(affairs ~ rating + children, data = d)
summary(lm3)
#>
#> Call:
#> lm(formula = affairs ~ rating + children, data = d)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.9246 -1.5072 -0.7014 -0.3280 11.6720
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4.3570 0.5657 7.702 5.57e-14 ***
#> rating -0.8058 0.1196 -6.739 3.76e-11 ***
#> childrenyes 0.3734 0.2921 1.278 0.202
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 3.168 on 598 degrees of freedom
#> Multiple R-squared: 0.08064, Adjusted R-squared: 0.07756
#> F-statistic: 26.23 on 2 and 598 DF, p-value: 1.209e-11d %>%
filter(children == "yes") %>%
lm(affairs ~ rating, data = .)
#>
#> Call:
#> lm(formula = affairs ~ rating, data = .)
#>
#> Coefficients:
#> (Intercept) rating
#> 5.0912 -0.90096.12 Rechnen Sie die Regression nur für “Halodries”; d.h. für Menschen mit Seitensprüngen. Dafür müssen Sie alle Menschen ohne Affären aus den Datensatz entfernen.
lm4 <- d %>%
filter(affairs > 0) %>%
lm(affairs ~ rating, data = .)
summary(lm4)
#>
#> Call:
#> lm(formula = affairs ~ rating, data = .)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -6.0605 -3.5157 -0.0605 3.6895 7.4843
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 8.7570 1.0225 8.564 1.3e-14 ***
#> rating -0.8483 0.2800 -3.030 0.00289 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 4.144 on 148 degrees of freedom
#> Multiple R-squared: 0.05841, Adjusted R-squared: 0.05205
#> F-statistic: 9.181 on 1 and 148 DF, p-value: 0.002887d3 <- d2 %>%
mutate(is_halodrie = affairs > 0)lm5 <- lm(rating ~ is_halodrie, data = d3)
summary(lm5)
#>
#> Call:
#> lm(formula = rating ~ is_halodrie, data = d3)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.09313 -0.44667 -0.09313 0.90687 1.55333
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4.09313 0.05029 81.394 < 2e-16 ***
#> is_halodrieTRUE -0.64646 0.10066 -6.422 2.74e-10 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.068 on 599 degrees of freedom
#> Multiple R-squared: 0.06442, Adjusted R-squared: 0.06286
#> F-statistic: 41.25 on 1 and 599 DF, p-value: 2.736e-10