1 Modellierung des Preises von Diamanten
In diesem Post untersuchen wir den Preis von Diamanten und gehen auf einige Aspekte der statistischen Modellierung ein.
Dieser Post orientiert sich an diesem Buchkapitel.
2 Pakete laden
library(tidyverse) # Datenjudo
library(corrr) # Korrelation
library(ggfortify) # Annahmen grafisch überprüfen
library(modelr) # Hilfen zum Modellieren
library(broom) # tidy Regressionsergebnisse3 Daten laden
data("diamonds")4 Datensatz verstehen
Ein zentraler Punkt in der statistischen Modellierung ist das Priori-Wissen: Dass man weiß, worüber man redet. Bei der Modellierung des Preises von Diamananten bietet sich an, etwas über dieses Sujet zu wissen – zumindenst die Variablen des Datensatzes zu verstehen.
Die Hilfeseite zum Datensatz ist dazu nützlich.
5 Modellierung
5.1 Modell 1
Auf Basis unseres Vorwissens (Priori-Wissens) gehen wir davon aus, dass das Gewicht eines Diamanten stark korreliert mit dem Preis:
diamonds %>%
select(price, carat) %>%
correlate() %>%
focus(price) # Fokus auf Preis
#> # A tibble: 1 x 2
#> term price
#> <chr> <dbl>
#> 1 carat 0.922Die hohe Korrelation belegt, dass wir auf einem guten Weg sind (zu sein scheinen).
Man könnte natürlich auch weiter schauen, und alle numerischen Variablen in die Korrelation mit dem Preis aufnehmen:
diamonds %>%
select(where(is.numeric)) %>%
correlate() %>%
focus(price) %>%
arrange(-abs(price))
#> # A tibble: 6 x 2
#> term price
#> <chr> <dbl>
#> 1 carat 0.922
#> 2 x 0.884
#> 3 y 0.865
#> 4 z 0.861
#> 5 table 0.127
#> 6 depth -0.01065.1.1 Modellgüte
lm1 <- lm(price ~ carat, data = diamonds)
summary(lm1)$r.squared
#> [1] 0.84933055.1.2 Überprüfung der Annahmen
autoplot(lm1)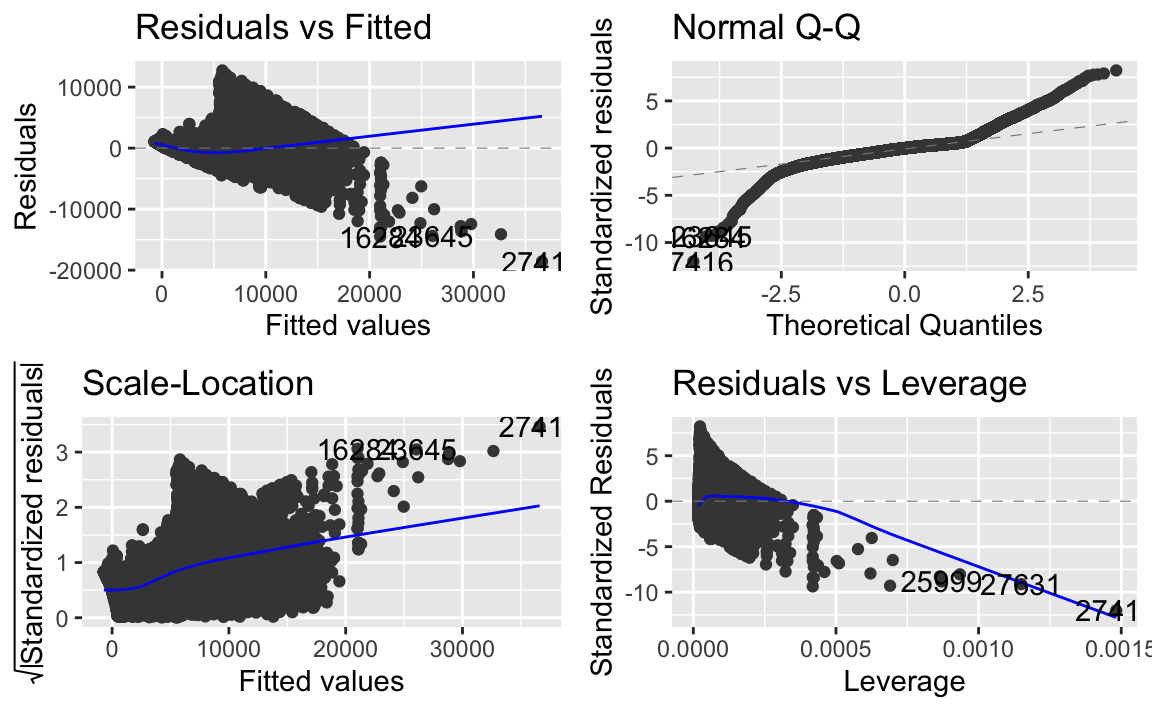
Oh je! Unser naiver Ansatz (naiv in der Rückschau) offenbart gravierende Mängel. Die vielleicht wichtigste Annahme im Regressionsmdell (aus mathematischer Sicht) ist, die Linearitätsannahme. Ist diese Annahme erfüllt, so sollten sich die Residen ohne Muster um die Nulllinie verteiilen. Wie wir im Diagramm 1 sehen, ist diese Annahme stark verletzt.
Probieren wir, es besser zu machen
5.2 Modell 2
5.2.1 Genauerer Blick auf den Zusammenhang
diamonds %>%
select(price, carat) %>%
ggplot(aes(x = carat, y = price)) +
geom_density2d()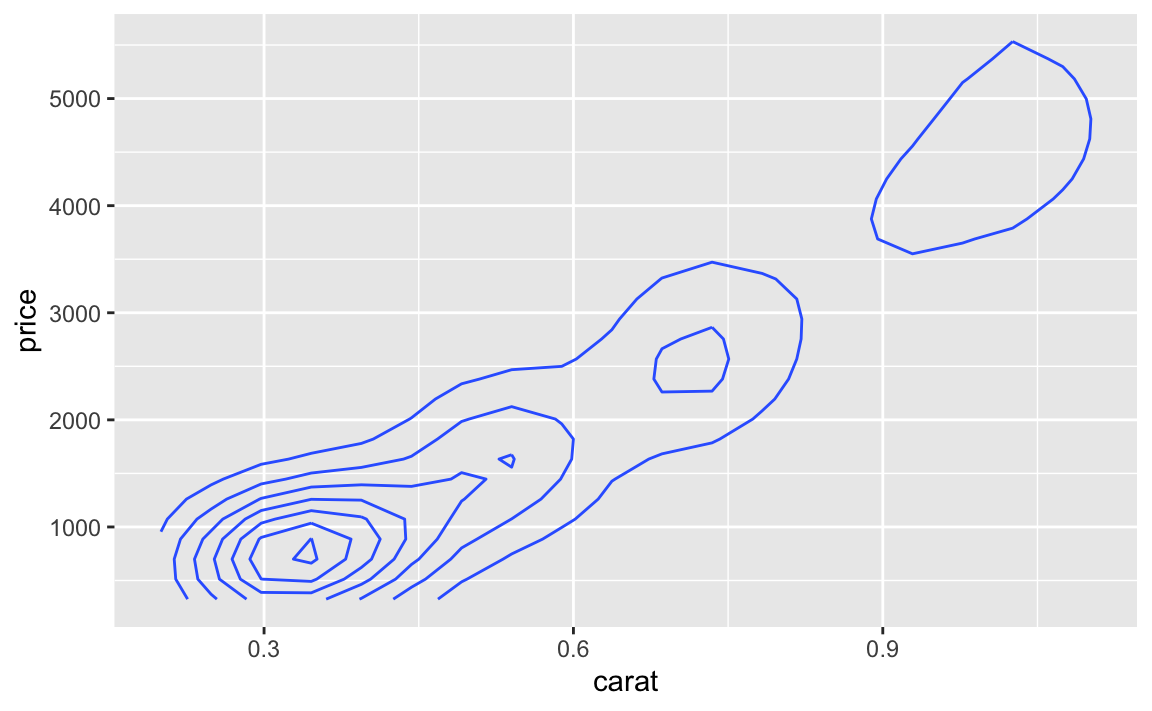
In den inneren Kreisen (Konturlinien) ist die Dichte an Diamanten am höchsten (dort sind die meisten Diamanten).
Oder, ähnlich:
diamonds %>%
select(price, carat) %>%
filter(percent_rank(price) < .9) %>% # nur die biligsten 90%
filter(percent_rank(carat) < .9) %>% # nur die kleinsten 90%
ggplot(aes(x = carat, y = price)) +
geom_density2d_filled()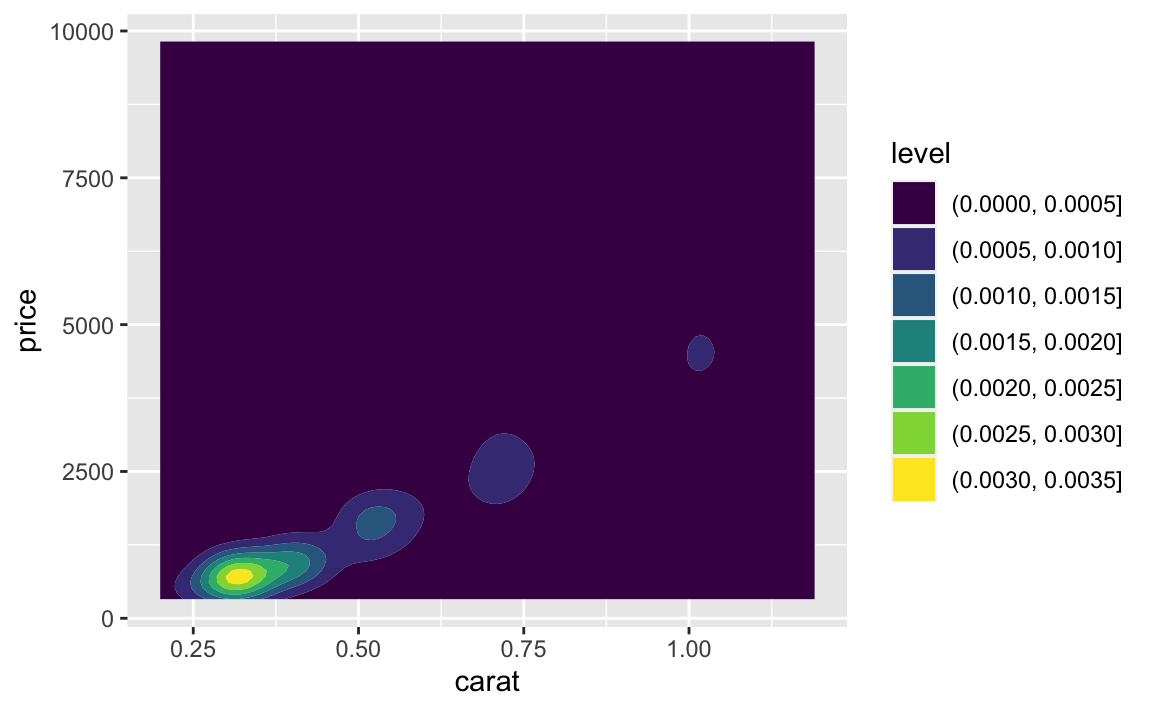
Vielleicht so:
diamonds %>%
select(price, carat) %>%
filter(percent_rank(price) < .95) %>% # nur die biligsten 95%
filter(percent_rank(carat) < .95) %>% # nur die kleinsten 95%
ggplot(aes(x = carat, y = price)) +
geom_hex(bins=50) +
geom_smooth()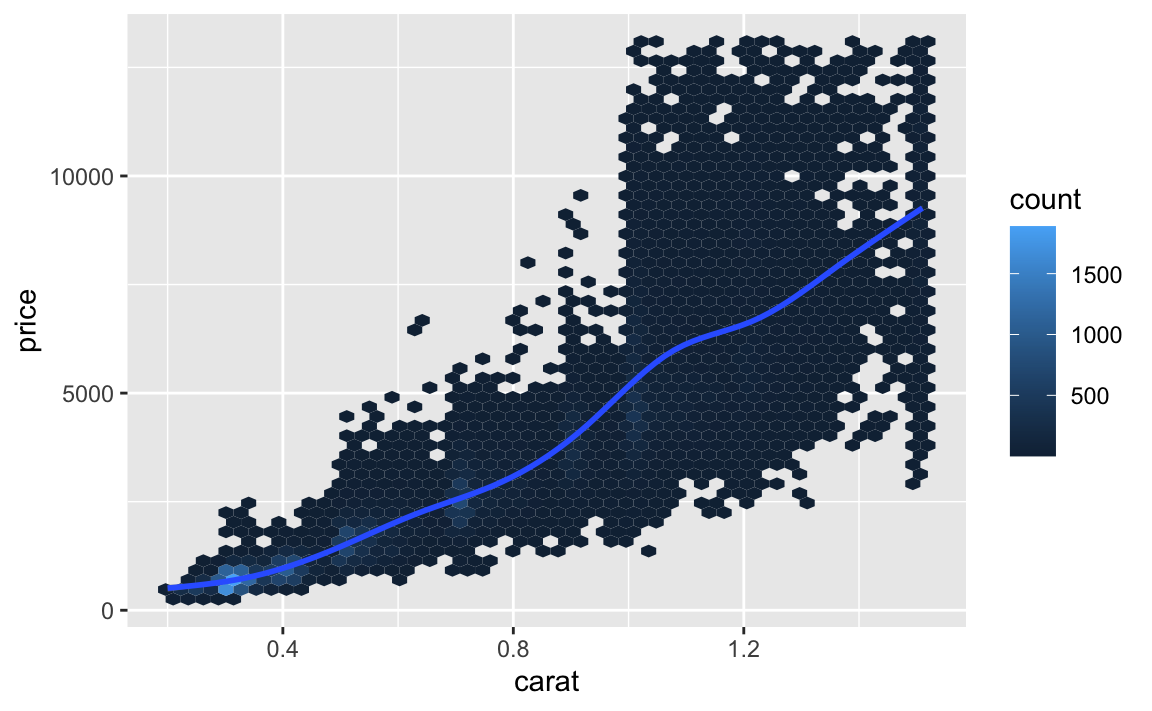
Es sieht so aus, als wäre der Zusammenhang nicht linear. Genau das hat uns auch das Diagramm oben gezeigt, bei dem Residuen gegen vorhergesagte Werte angezeichnet wurden.
5.2.2 Log-Modell
Ein Log-Modell geht von einem multiplikativen (exponentiellen) Zusammenhang aus: Wächst X um einen festen Betrag, so wächst Y um einen festen Faktor.
lm2 <- lm(log(price) ~ carat, data = diamonds)
summary(lm2)$r.squared
#> [1] 0.8467802autoplot(lm2, which = 1)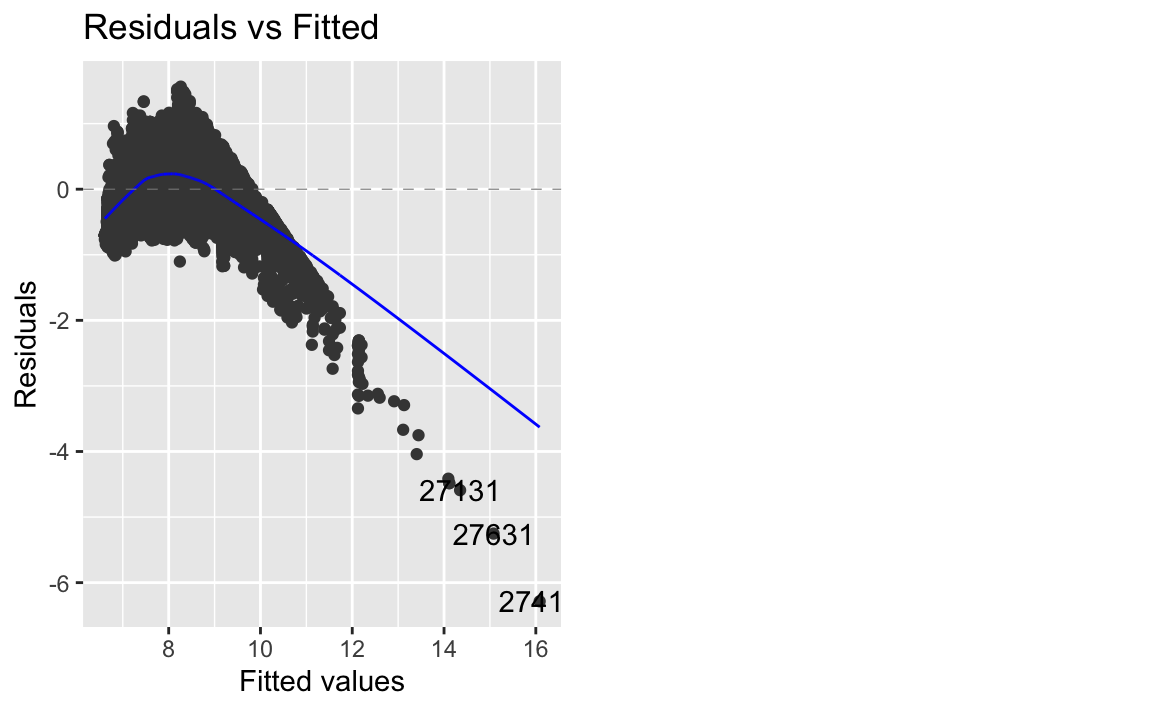
Das Modell scheint auch noch nicht so gut zu passen.
5.3 Modell 3
Vielleicht wird der Preis von einem Diamanten eher so berechnet: Steigt das Gewicht des Diamanten um 1%, so steigt der Preis um 1% (oder x$)?
diamonds <-
diamonds %>%
mutate(price_log = log2(price),
carat_log = log2(carat))ggplot(diamonds) +
aes(x = carat_log, y = price_log) +
geom_hex(bins=50)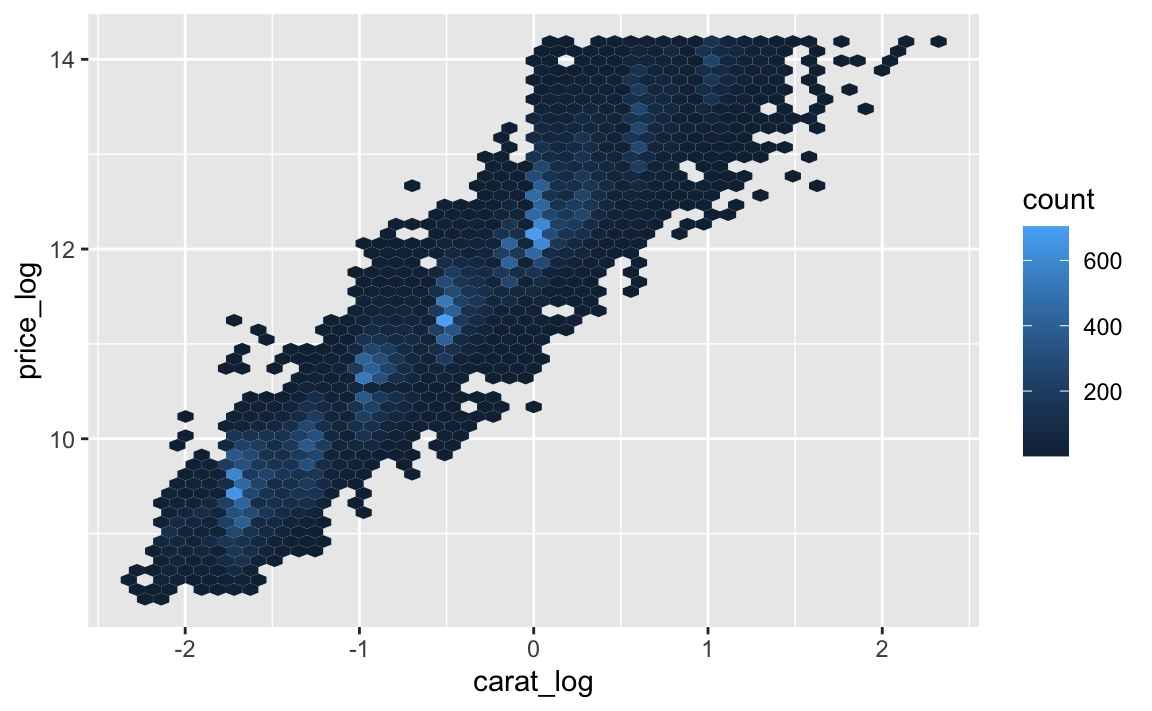
Das ist ein schöner, lineare Trend! Das Log-Log-Modell für Preis und Karat passt!
5.3.1 Modellgüte
Übrigens ist ein Streudiagramm bei vielen Punkten (>1000) wegen des Overplottings nur bedingt geeignet. Ein Geom Hex ist hier nützlicher.
lm3 <- lm(price_log ~ carat_log, data = diamonds)
summary(lm3)$r.squared
#> [1] 0.9329893Tragen wir die Vorhersagen dieses Modells in die Daten ein:
diamonds %>%
add_predictions(lm3, "pred_lm3") %>%
mutate(pred_lm3_delog = 2^pred_lm3) %>%
ggplot() +
geom_hex(aes(x = carat, y = price)) +
geom_line(aes(x = carat, y = pred_lm3_delog),
color = "red") +
lims(x = c(0,2.5), y = c(0, 20000))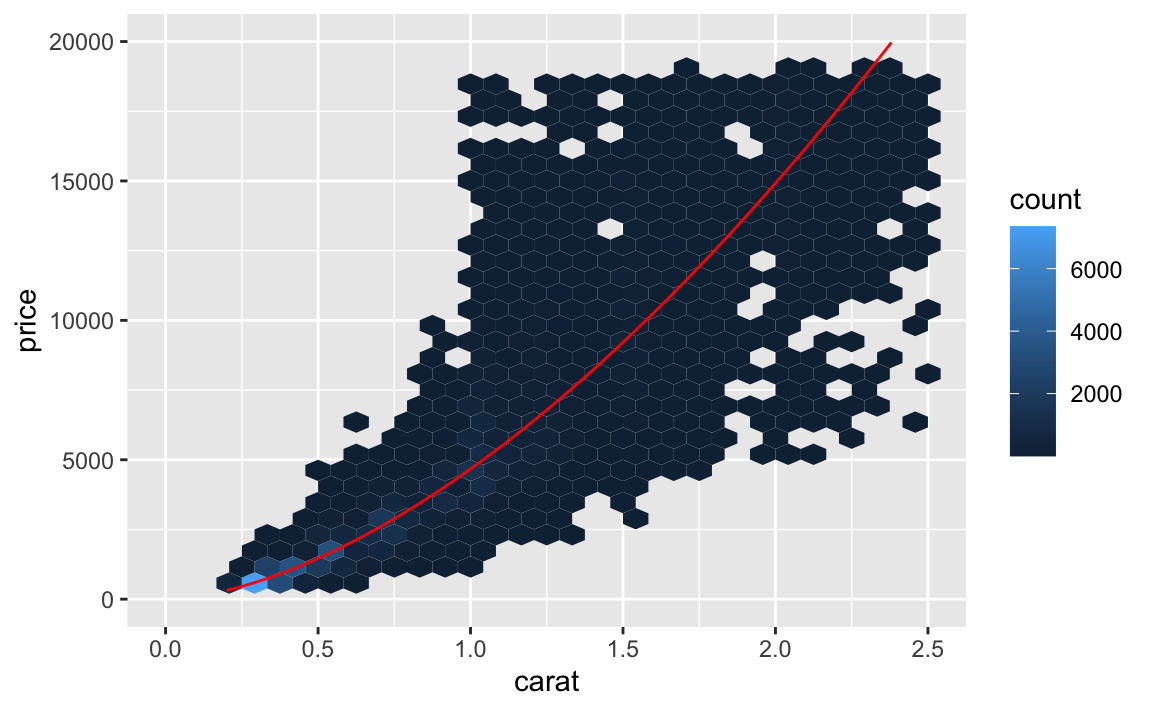
5.3.2 Voraussetzungen prüfen
autoplot(lm3, which = 1)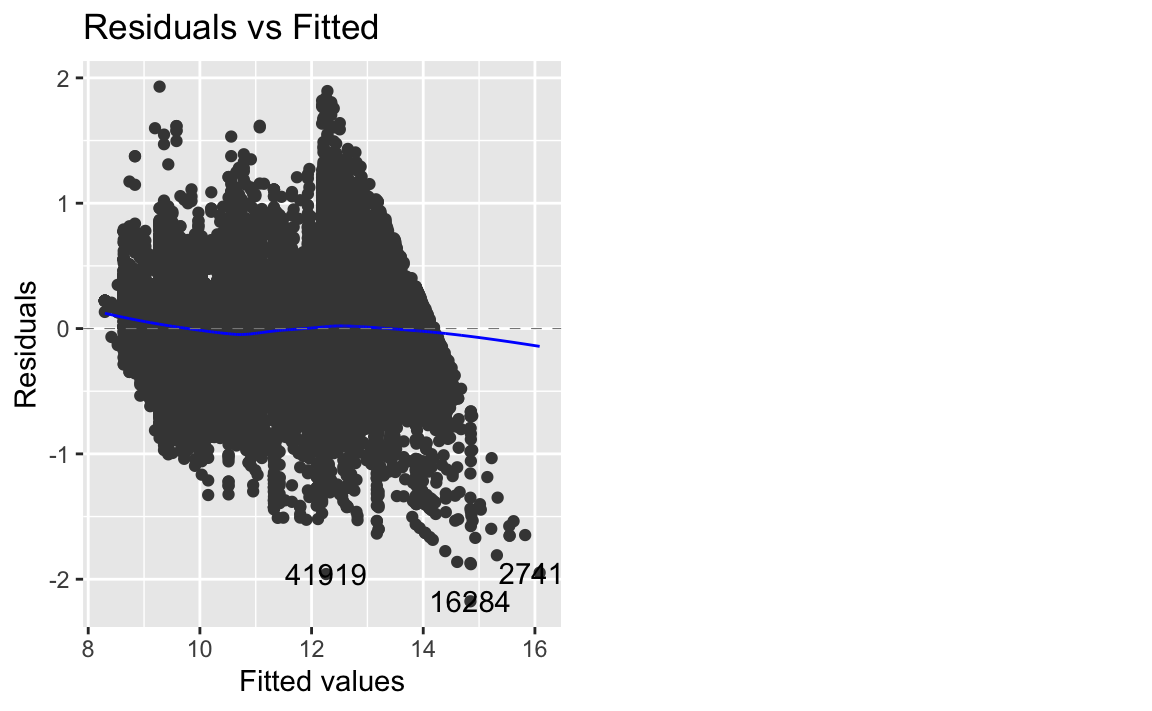
Die “abrasierte Kante” kommt vermutlich von unserem Filter. Leider lässt die große Anzahl der Punkte das Diagramm nur bedingt nützlich erscheinen; wir können wegen des Overplotting nicht wirklich gut einen Trend sehen. Aber was wir sehen, ist zumindest besser als in den vorherigen Modellen. Fortschritt!
5.4 Modell 3a und 4
5.4.1 Konfundierung von Schliff und Karat
Versuchen wir zu verstehen, welche Variablen noch eine Rolle spielen. Schliff erscheint einem Laien als plausibler Prädiktor. Schauen wir uns Schliff näher an.
diamonds %>%
select(cut, price) %>%
ggplot(aes(x = cut, y = price)) +
geom_boxplot()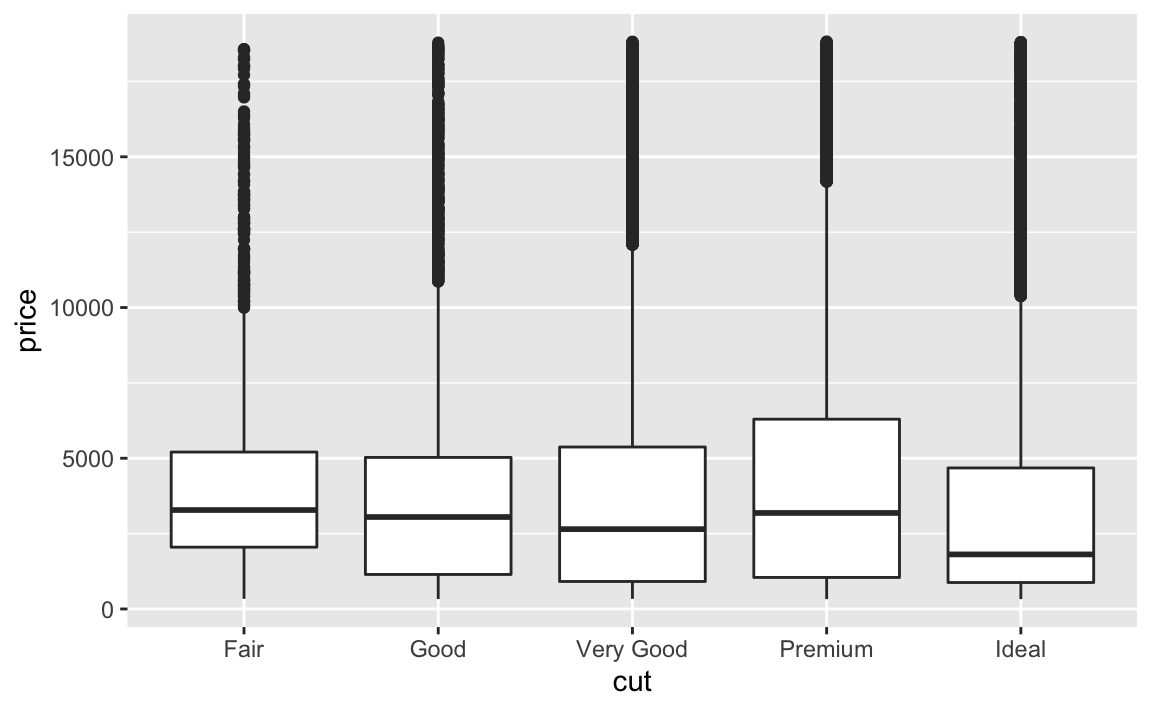
Verblüffend! Die guten Schliffarten erzielen nicht den besten Preis! Im Gegenteil: der schlechteste Schliff (Fair) erzielt den höchsten Preis. Wie kann das sein?
Ein (plausibler) Grund ist, dass Schliff und Karat konfundiert sind: Schwerere Diamanten (hohe Karatzahl) hätten demnach einen schlechteren Schliff. Da aber Karat und Preis positiv korreliert sind, sind Diamanten schlechteren Schliffs teuerer. Soweit die Theorie. Untersuchen wir diese These in den Daten. Dazu betrachten wir den Preis relativ zur Karatzahl. Wir untersuchen also die Frage: Im Verhältnis zu seiner Karatzahl, wie teuer ist der Diamant? Damit können wir prüfen, ob ein Diamant mit schlechtem Schliff im Verhältnis zu seinem Gewicht wirklich (überdurchschnittlich) teuer ist. Wenn unsere These stimmt, müsste dann ein Diamant schlechten Schliffs günstiger sein.
diamonds %>%
add_residuals(lm3, "resid_lm3") %>%
ggplot(aes(x = cut, y = resid_lm3)) +
geom_boxplot()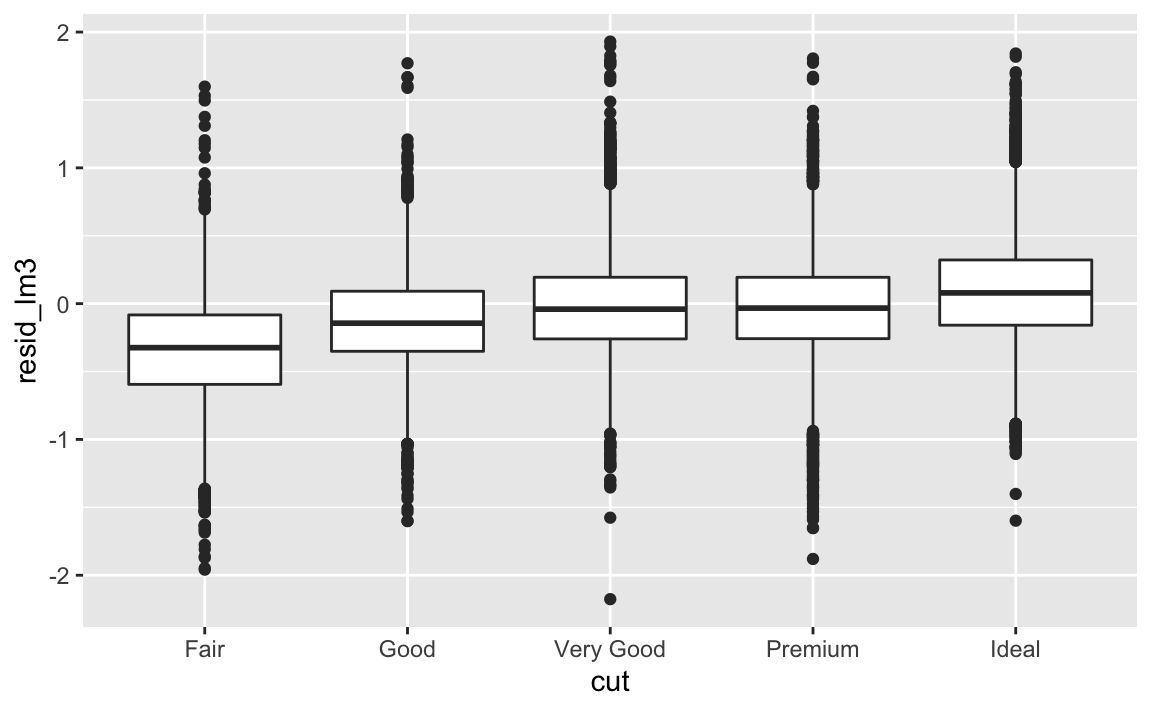
Bingo! Unsere Theorie scheint richtig zu sein. Zumindest passen die Daten zu unserer Vorhersage: Jetzt sind die Diamanten schlechten Schliffs billiger als es ihre Karatzahl vermuten ließe. Anders gesagt: Betrachtet man nur Diamanten mit einer bestimmten Karatzahl, so sind in dieser Gruppe die Diamanten schlechten Schliffs günstiger als Diamanten besseren Schliffs (und entsprechend für Diamanten anderen Schliffs).
5.4.2 lm3a
Ergänzen wir ein Modell, lm3a, welches cut zusätzlich zum Gewicht (Karat) eines Diamannten nutzt, um den Preis vorherzusagen.
lm3a <- lm(price_log ~ carat_log + cut, data = diamonds)
summary(lm3a)$r.squared
#> [1] 0.9371003Ah, ein sehr hoher \(R^2\)-Wert.
Was sind die Vorhersagen für die Werte von cut von unserem Modell, lm3a?
So können wir uns für die Werte von cut auf Basis von lm3 eine Vorhersage geben lassen. Dabei nehmen wir den typischen Wert von Karat (log), den Median, um genau zu sein:
lm3a_grid <-
diamonds %>%
data_grid(cut, .model = lm3a) %>%
add_predictions(lm3a)
lm3a_grid
#> # A tibble: 5 x 3
#> cut carat_log pred
#> <ord> <dbl> <dbl>
#> 1 Fair -0.515 11.0
#> 2 Good -0.515 11.2
#> 3 Very Good -0.515 11.3
#> 4 Premium -0.515 11.3
#> 5 Ideal -0.515 11.4Visualisieren wir den vorhergesagten Preis laut Karatzahl und Schliffart (von lm3a) als rote Punkte und setzen die Verteilung der Preise in Abhängigkeit der Schliffart dagegen (Boxplots):
diamonds %>%
ggplot() +
geom_boxplot(aes(x = cut,
y = price_log)) +
geom_point(data = lm3a_grid,
aes(x = cut,
y = pred),
color = "red",
size = 5)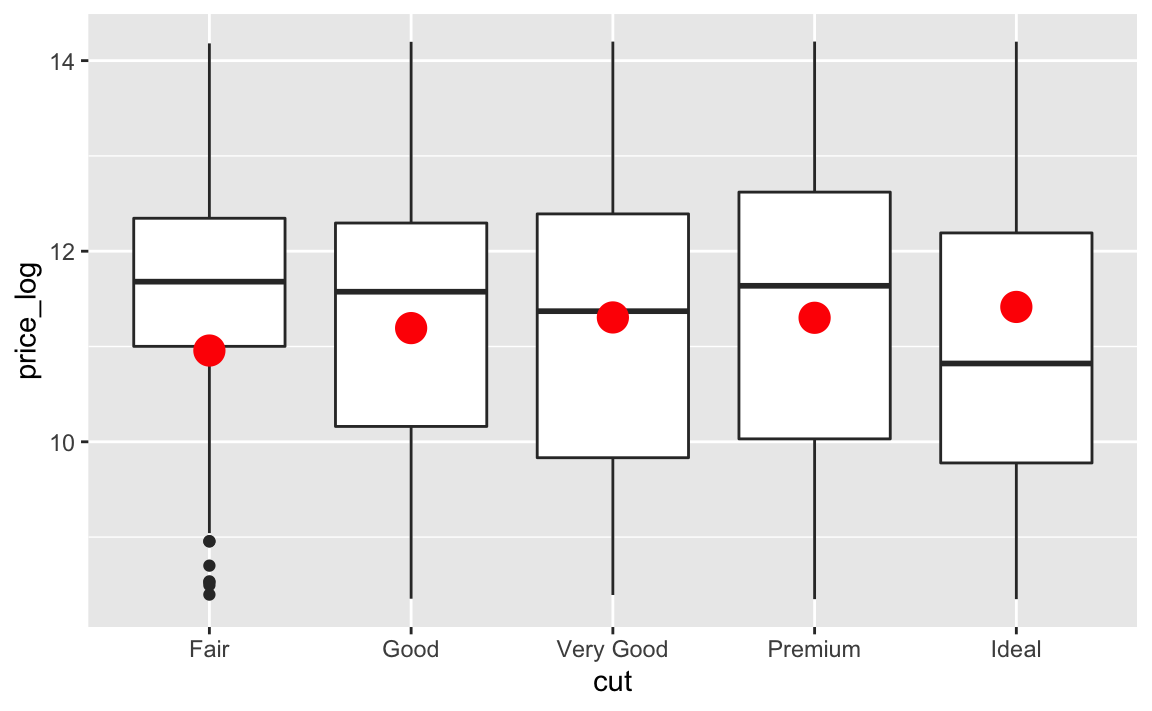
Wir sehen, dass der Preis laut Karatzahl bei schlechter Schliffart (Fair) höher sein müsste: Relativ zur Karatzahl sind diese Diamanten günstig.
5.4.3 lm4: Schliff als Prädiktor
Umgekehrt können wir auch anschauen, ob die Karatzahl mit dem Preis relativ zur Schliffart zusammenhängt. Definieren wir dazu ein Modell, das nur die Schliffart zur Vorhersage des Preises nutzt:
lm4 <- lm(price_log ~ cut, data = diamonds)
summary(lm4)$r.squared
#> [1] 0.01813734diamonds <-
diamonds %>%
add_residuals(lm4, "resid_lm4")diamonds %>%
ggplot() +
aes(x = carat_log, y = resid_lm4) +
geom_hex(bins = 50)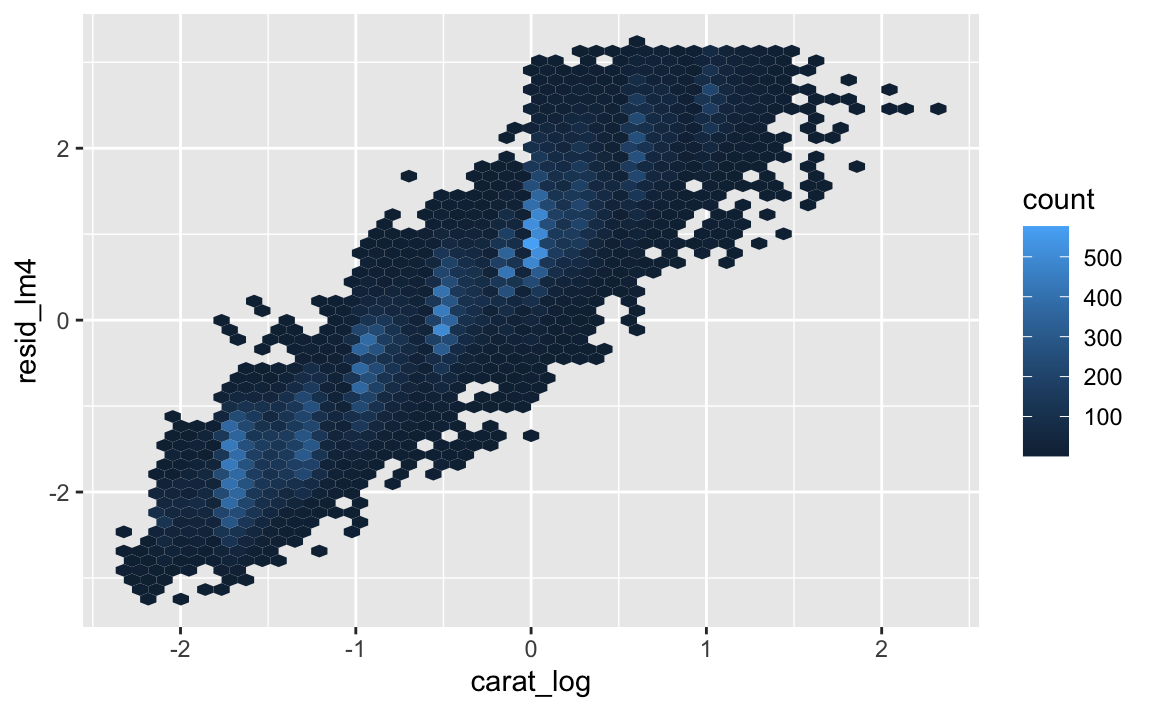
Es ist kein großer Unterschied zu erkennen. Der Zusammenhang von Preis und Karat (jeweils log2) ist praktisch gleich zum Zusammenang des Preises relativ zur Schliffart und Karat. Das zeigt, dass die Schliffart nicht wirklich einen “eigenen” Zusammenhang mit dem Preis hat, der über den Zusammenhang der Karatzahl hinausgeht.
Alternativ könnte man den Zusammenhang von Karat und Preis relativ zur Schliffart auch so betrachten:
diamonds %>%
ggplot(aes(x = carat_log, y = price_log)) +
facet_wrap(~ cut) +
geom_ref_line(v = 0) +
geom_ref_line(h = 10) +
geom_hex(bins = 50)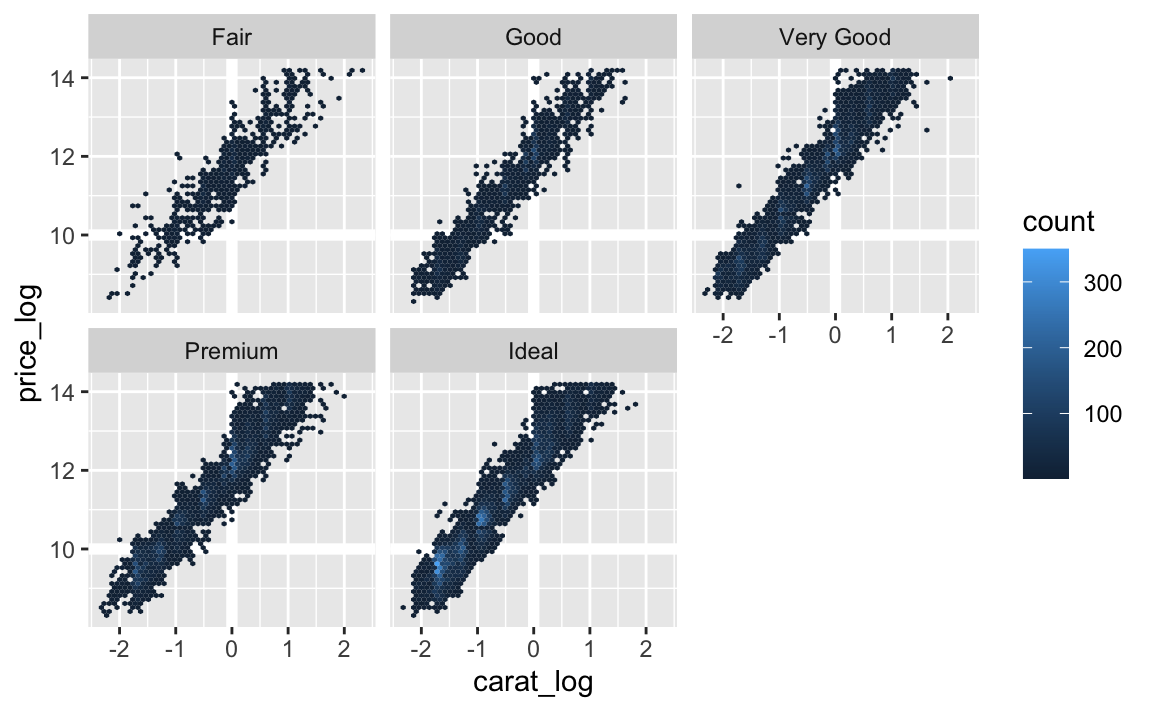
Die Diagramme sehen ähnlich aus: Unabhängig von der Schliffart (was in jeder einzelnen Facette der Fall ist) ist der Zusammenhang von Karat und Preis stark. Anstelle von “unabhängig von” sagt man auch “bereinigt von”, also “bereinigt von der Schliffart”, ist der Zusammenhang von Karat und Preis weiterhin stark.
Die Referenzlinien wurden hinzugefügt, um einen “Referanzrahmen” zu geben: \(x=0\) entspricht \(2^0=1\) Karat; \(y=2^10=1024\) Dollar Preis.
5.4.4 Modellkoeffizienten
Die relative Bedeutung des Prädiktoren lässt sich mit einem (ggf. standardisierten) Regressionskoeffizienten darstellen (hier nicht weiter ausgeführt).
tidy(lm3a)
#> # A tibble: 6 x 5
#> term estimate std.error statistic p.value
#> <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 (Intercept) 12.1 0.00250 4836. 0
#> 2 carat_log 1.70 0.00191 888. 0
#> 3 cut.L 0.324 0.00635 51.0 0
#> 4 cut.Q -0.0958 0.00562 -17.1 4.80e-65
#> 5 cut.C 0.0763 0.00491 15.6 2.09e-54
#> 6 cut^4 0.0269 0.00394 6.81 9.60e-125.4.5 \(R^2\) zur Beurteilung der Relevanz von Prädiktoren
Alternativ kann man den Zuwachs an \(R^2\) anschauen, wenn man Prädiktoren hinzufügt.
summary(lm3)$r.squared
#> [1] 0.9329893summary(lm3a)$r.squared
#> [1] 0.9371003Der zusätzliche Prädiktor in lm3a scheint wenig Zuwachs in der Modellgüte (gemessen in \(R^2\)) einzubringen. Die unique Releanz des zweiten Prädiktors (cut) ist somit nicht so hoch.
6 Fazit: “Händische” Modellierung
Wir haben uns einige Mühe gemacht, den Datensatz zu verstehen. Dazu haben wir Vorwissen eingebracht und analysiert, welche Muster übrig bleiben, wenn wir ein bestimmtes Muster “abschälen”. So versuchten wir, die mehreren “Schichten” an Mustern zu erkennen, die bei der Preisgestaltung von Diamanten eine Rolle spielen. Gerade schwächere Muster werden oft von einem stärkeren Muster übertönt. Um auch das schwächere Muster zu erkennen, muss man das stärkere Muster entfernen. Das geht mittels der Regressionsanalyse. Allerdings ist die Visualisierung eine zentrale Stütze, um zu verstehen, was im Datensatz “passiert”. Es zeigt sich, dass eine gesunde Portion Datenjudo immer nützlicht ist.
6.1 Maschinelle Prädiktorenwahl
Eine Alternative zur manuellen Wahl von Prädiktoren wie oben ausgeführt, ist die maschinelle Auswahl, etwa mittels schrittweiser Regression. Solche Methoden haben ihre Stärken, aber sie haben auch Nachteile. Erstens sind die resultierenden Modelle “schwarze Kisten”; man spricht von “black box models”. Es ist immer nützlich, und manchmal unentbehrlich, zu verstehen, warum ein Modell eine bestimmte Vorhersage trifft. So würde es z.B. vor Gericht wohl nicht reichen, Ihre Entscheidung zu begründen mit “der Computer hat gesagt, es könnte ein gutes Ergebnis bringen”. Diese Begründung reicht deshalb nicht, weil es keine Begründung ist. Zweitens sind Modelle, bei denen man die Wirkweise, zumindest in Ansätzen versteht, robuster als Black-Box-Modelle. Häufig ändern sich Daten, Verteilungen oder Zusammenhänge. Kennt man die Zusammenhänge, gar die kausalen Zusammenhänge, so wird das Modell bei Verschiebungen seiner Grundlagen robuster bleiben als ein Black-Box-Modell. Einige Aspekte wird ein maschinell gewähltes Modell nicht aufdecken bzw. verwenden (z.B. Dublikate bei den Diamanten, ob es da wohl welche gibt?).
6.2 Einreichen
In einem Prognose-Wettbewerb wählen Sie Ihr bestes Modell (beste Prognosegüte) aus, und reichen dessen Vorhersage ein, zusammen mit einer ID pro Beobachtung, so dass man weiß, auf welchen Diamanten sich ein vorhergesagter Preis bezieht.