1 Hintergrund und Ziel

In diesem Post sagen wir den Preis von Diamanten vorher. Nehmen wir an, Sie hätten bei einem großen Online-Kaufhaus angeheuert und ihre Chefin möchte gerne wissen, welchen Preis sie wohl für bestimmte Diamanten erzielen kann. price ist also die vorherzusagende Größe im Datensatz diamonds (aus ggplot2).

2 Pakete laden

library(tidyverse)  # data wrangling
library(tidymodels)  # Vorhersagemodellierung
library(modelr)  # Modellierungshilfen
library(lvplot)  # letter value plots

3 Daten laden

data(diamonds)  # aus dem Paket `ggplot2`

4 Aufteilen in Train- und Test-Datensatz

Wir trennen einen Teil (25%) des Datensatzes ab, um zu simulieren, dass wir diese Daten erst in der Zukunft zu sehen bekommen werden. Letztlich geht es ja bei der Vorhersagemodellierung darum, Werte in der Zukunft vorherzusagen.

Ein einfacher Weg dazu sieht so aus:

diamonds <-
  diamonds %>% 
  mutate(id = row_number())

train <-
  diamonds %>% 
  slice_sample(prop = .75)

test <-
  diamonds %>% 
  anti_join(train, by = "id")

Ingesamt entspricht die Zeilenzahl der zwei Teile (train und test) der Gesamtzeilenzahl:

nrow(test) + nrow(train) == nrow(diamonds)
#> [1] TRUE

Alternativ kann man auch z.B. folgende Komfort-Funktion verwenden:

flights_index <- initial_split(diamonds)

train <- training(flights_index)
test <- testing(flights_index)

5 EDA

Hier nicht ausgeführt…

In diesem Teil versuchen Sie, den Datensatz zu “verstehen”. Typische Fragen, die Sie in diesem Zusammenhang untersuchen sind:

• Wie ist die Verteilung der abhängigen Variable? Was sind ihre typischen und untypischen Werte, wie ihre Streuung?
• Welche Variablen stehen (in welcher funktionalen Form) mit der abhängigen Variablen (und wie stark) in Zusammenhang?
• Sind die Zusammenhänge abhängig von Drittvariablen (und wie sehr)?
• Wie viele fehlenden Variablen gibt es bei welchen Variablen und inwieweit begrenzen Sie (prognoszierende) Modelle?
• Finden sich “merkwürdige” Werte, die u.U. auf Fehler oder besondere Prozesse zurückzuführen sind?
• Welche kausalen Theorien könnten die beobachteten Zusammenhänge erklären?

6 Modellierung

Auf geht’s! Erstellen wir ein paar Modelle!

lm1 <- lm(price ~ carat + depth + table + cut + color,
          data = train)

summary(lm1)$r.squared
#> [1] 0.8717391

lm2 <- lm(price ~ carat^2 + carat + depth + table + cut + color + carat:cut,data = train)

summary(lm2)$r.squared
#> [1] 0.8737339

7 Vorhersage im Test-Datensatz

test2 <-
  test %>% 
  add_predictions(model = lm1, var = "pred_lm1") %>% 
  add_predictions(model = lm2, var = "pred_lm2")

test2 %>% 
  select(pred_lm1, pred_lm2, price) %>% 
  pivot_longer(cols = c(pred_lm1, pred_lm2), 
               names_to = "model",
               values_to = "pred") %>% 
  ggplot() +
  geom_density(aes(x = price), 
               fill = "grey50",
               alpha = .5) +
  geom_density(aes(x = pred, 
                   fill = model),alpha = .5
               )

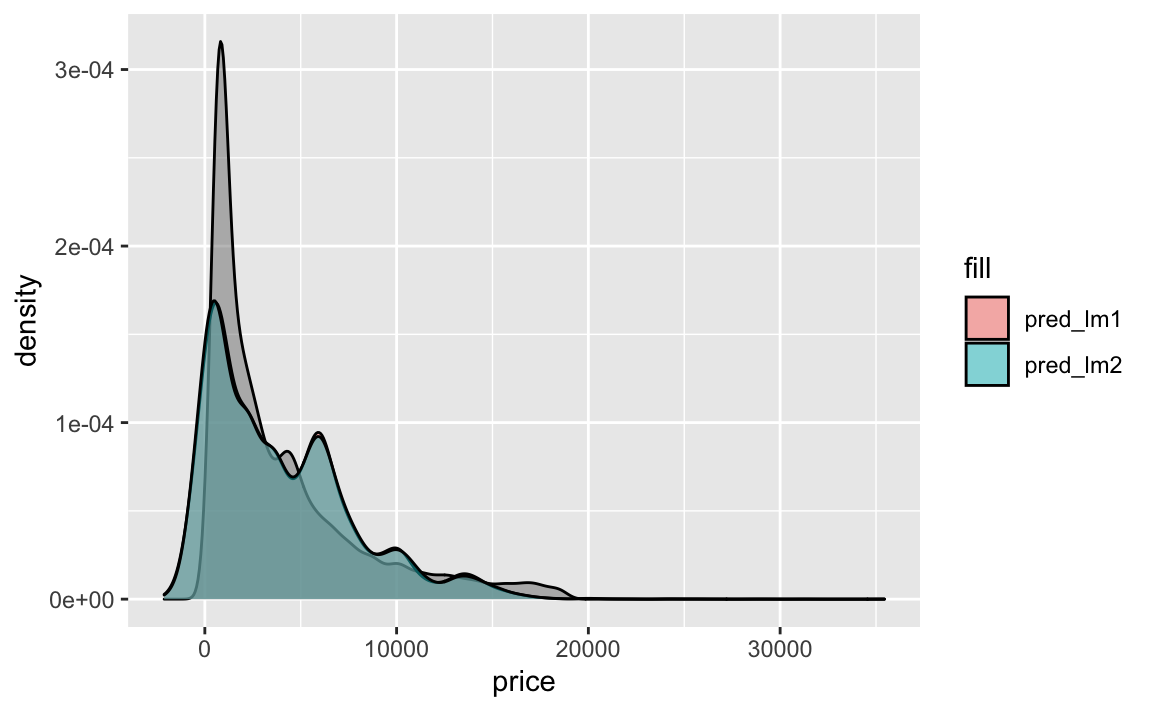
Das Diagramm zeigt, dass die beiden Modelle lm1 und lm2 fast identische Vorhersagen liefern. Allerdings haben beide Modelle negative Preise, was nicht wirklich Sinn macht. Letzteres zeigt folgendes Diagramm besser:

test2 %>% 
  select(pred_lm1, pred_lm2, price) %>% 
  pivot_longer(everything(), 
               names_to = "model",
               values_to = "pred") %>% 
  ggplot() +
  geom_ref_line(h = 0) +
  aes(x = model, y = pred, fill = model) +
  geom_boxplot() 
  

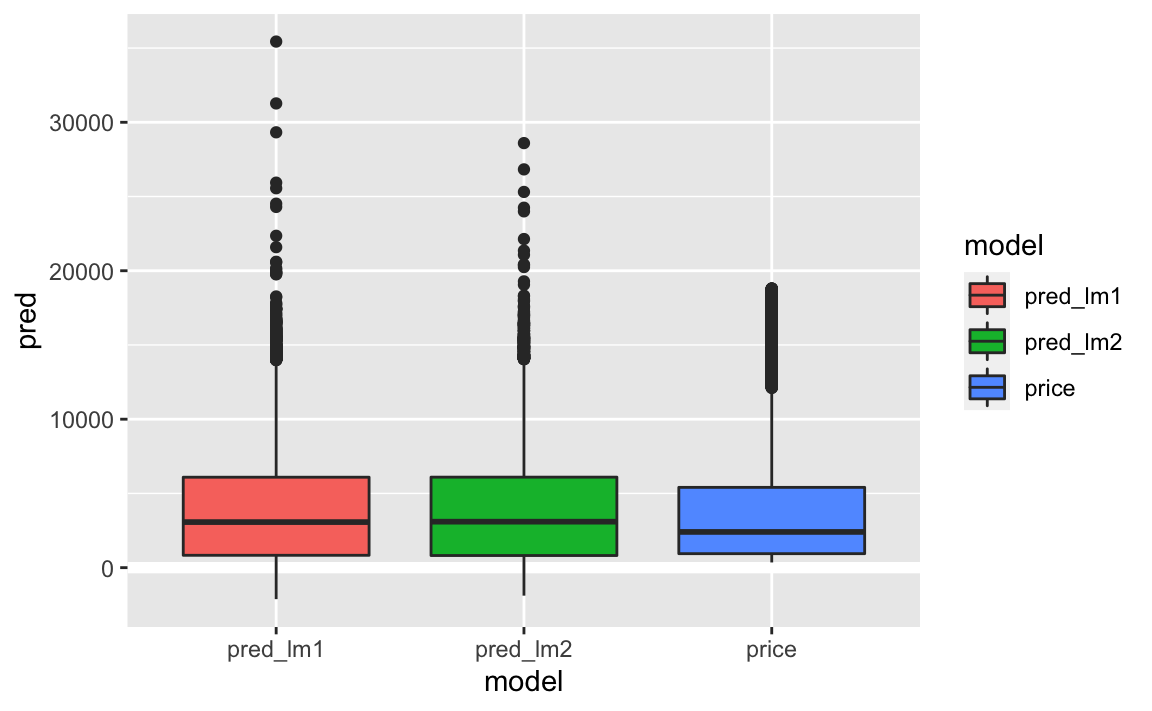
Im Letter value plot kommt die Schiefe und die Extremwerte differenzierter zum Vorschein.

test2 %>% 
  select(pred_lm1, pred_lm2, price) %>% 
  pivot_longer(everything(), 
               names_to = "model",
               values_to = "pred") %>% 
  ggplot() +
  geom_ref_line(h = 0) +
  aes(x = model, y = pred, fill = model) +
  geom_lv() 
  

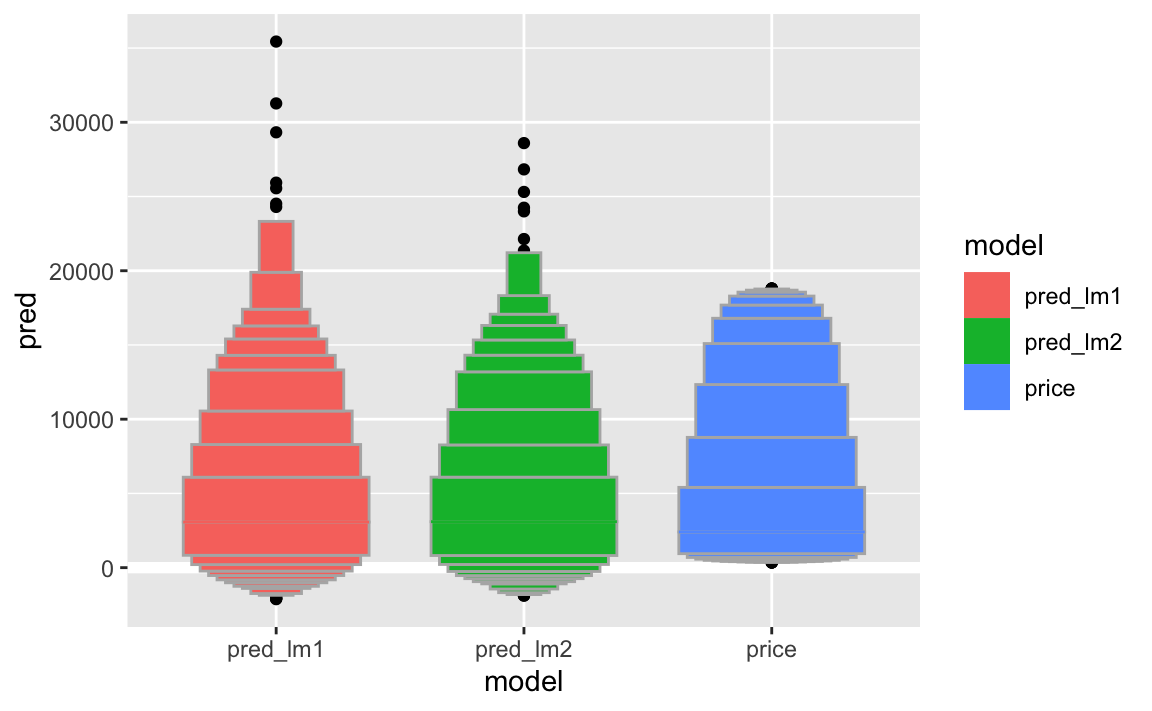
8 R-Quadrat im Test-Datensatz

test2 %>% 
  summarise(
    rsq_lm1 = rsq_vec(truth = price, estimate = pred_lm1),
    rsq_lm2 = rsq_vec(truth = price, estimate = pred_lm2)
    )
#> # A tibble: 1 x 2
#>   rsq_lm1 rsq_lm2
#>     <dbl>   <dbl>
#> 1   0.871   0.875

Die beiden Modelle sind fast identisch in ihrem R-Quadrat. Daher bietet es sich an, das einfachere Modell zu bevorzugen.

9 Weitere Überlegungen

Viele Anknüpfungspunkte bieten sich; viele Wege sind noch nicht erforscht. Eine Idee ist, dass die Schätzung von R-Quadrat im Test-Datensatz von der Zufälligkeit der Aufteilung des Gesamt-Datensatz abhängig ist. Hier könnte man verschiedene Aufteilungen vergleichen (Stichwort: Kreuzvalidierung).

Dann wurden nur wenige Modelle betrachtet und diese nicht stichhaltig begründet. Man könnte sich noch viele weitere Varianten des linearen Modells anschauen oder Annahmen des linearen Modells aufgeben, so etwa multiplikative Modelle (Stichwort: Log-Tranformation).

Ein weiterer Ansatz ist, auf automatisierte Modellwahl zu betreiben, etwa auf Basis der schrittweisen Regression.

10 Einreichen

Sie reichen dann einen Datensatz mit den Vorhersagen Ihres Modells für den Test-Datensatz ein. Im Gegensatz zum Beispiel hier wissen Sie nicht wie präzise Ihre Vorhersagen sind. Aber so ist es im Leben: Ob eine Idee gut war, weiß man immer erst hinterher 🤪🕺😬.

Einreichen <-
  test2 %>% 
  select(id, pred_lm1)

head(Einreichen)
#> # A tibble: 6 x 2
#>      id pred_lm1
#>   <int>    <dbl>
#> 1    19   -2062.
#> 2    22    -462.
#> 3    26    -411.
#> 4    27   -1475.
#> 5    31    -318.
#> 6    38    -764.