- 1 Hintergrund und Forschungsfrage
- 2 Pakete laden
- 3 Daten laden
- 4 flights2: Nicht benötigte Variablen entfernen und ID hinzufügen
- 5 Aufteilung in Train- und Testsample
- 6 flights_train2, flights_test2
- 7 lm0: Nullmodell
- 8 lm1: origin
- 9 lm2: All in
- 10 flights_train3: Textvariablen in Faktorvariablen umwandeln
- 11 flights_train4: Faktorstufen zusammenfassen
- 12 lm3: Alle zusammengefassten Faktorvariablen
- 13 lm4: Alle metrischen Variablen
- 14 lm5: Alle metrischen und alle (zusammengefassten) nominalen Variablen
- 15 Wetter-Daten ergänzen
- 16 flights_train6
- 17 lm6: Plus Wetterdaten
- 18 lm7: Rohe Gewalt
- 19 lm8: Bestes Modell aus der Best-Subset-Analyse
- 20 Prüfen der Modellqualität
- 21 Einreichen
- 22 Was noch?
- 23 Tidymodels
- 24 Reproducibility
1 Hintergrund und Forschungsfrage
Wir untersuchen die Forschungsfrage Was sind Prädiktoren von Flugverspätungen. Dazu nutzen wir lineare Modelle als Modellierungsmethoden.
Dieser Post knüpft an den Post zur explorativen Datenanalyse der Flugverspätungen an (es gibt auch hier, Teil 1 und hier, Teil 2 ein Video zu diesem EDA-Post).
2 Pakete laden
library("tidymodels") # Datenmodellierung
library("tidyverse") # data wrangling
library("conflicted") # Name clashes finden
library("leaps") # Rohe Gewalt
library("skimr") # deskriptive Statistiken komfortabel
library("ggfortify") # Modellannahmen grafisch prüfen
library("tictoc") # Rechenzeit messen3 Daten laden
library("nycflights13")
data(flights)4 flights2: Nicht benötigte Variablen entfernen und ID hinzufügen
flights2 <-
flights %>%
select(-c(year, arr_delay)) %>%
drop_na(dep_delay) %>%
mutate(id = row_number()) %>%
select(id, everything()) # id nach vorne ziehen5 Aufteilung in Train- und Testsample
Der Hintergrund zur Idee der Aufteilung in Train- und Test-Stichprobe kann z.b. hier oder hier, Kapitel 15, nachgelesen werden.
flights_split <- initial_split(flights2,
strata = dep_delay,
na.rm = TRUE)6 flights_train2, flights_test2
set.seed(42) # Reproduzierbarkeit
flights_train2 <- training(flights_split)
flights_test2 <- testing(flights_split)Die “wirkliche Welt” (was immer das ist) besorgt die Aufteilung von Train- und Test-Sampel für Sie automatisch. Sagen wir, Sie arbeiten für die Flughafen-Aufsicht von New York. Dann haben Sie einen Erfahrungsschatz an Flügen aus der Vergangenheit in Ihrer Datenbank (Train-Sample). Einige Tages kommt Ihr Chef zu Ihnen und sagt: “Rechnen Sie mir mal die zu erwartende Verspätung der Flüge im nächsten Monat aus!”. Da heute nicht klar ist, wie die Verspätung der Flüge in der Zukunft (nächsten Monat) sein wird, stellen die Flüge des nächsten Monats das Test-Sample dar.
Übrigens: In der Prüfung besorgt das Aufteilen von Train- und Test-Sample netterweise Ihr Dozent…
7 lm0: Nullmodell
Eigentlich nicht nötig, das Nullmodell, primär aus didaktischen Gründen berechnet, um zu zeigen, dass in diesem Fall \(R^2\) wirklich gleich Null ist.
lm0 <- lm(dep_delay ~ 1, data = flights_train2)
glance(lm0)| r.squared | adj.r.squared | sigma | statistic | p.value | df | logLik | AIC | BIC | deviance | df.residual | nobs |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 40.14855 | NA | NA | NA | -1259418 | 2518840 | 2518861 | 397152640 | 246387 | 246388 |
Mit glance bekommt man das \(R^2\) (neben einem Haufen anderen Zeugs, was wir jetzt nicht brauchen). Man könnte z.B. auch summary(lm1) out arm::display(lm1). Es gibt verschiedene Möglichkeiten.
8 lm1: origin
lm1 <- lm(dep_delay ~ origin, data = flights_train2)tidy(lm1) # tidy zeit die (geschätzten) Regressionsgewichte (Betas)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 15.132723 | 0.1350185 | 112.07890 | 0 |
| originJFK | -3.084897 | 0.1944907 | -15.86141 | 0 |
| originLGA | -4.846399 | 0.1983607 | -24.43226 | 0 |
Man vergleiche:
flights_train2 %>%
drop_na(dep_delay) %>%
group_by(origin) %>%
summarise(delay_avg = mean(dep_delay)) %>%
mutate(delay_delta = delay_avg - delay_avg[1])| origin | delay_avg | delay_delta |
|---|---|---|
| EWR | 15.13272 | 0.000000 |
| JFK | 12.04783 | -3.084897 |
| LGA | 10.28632 | -4.846399 |
Der Mittelwertsvergleich und das Modell lm1 sind faktisch informationsgleich.
Aber leider ist es um die Modellgüte nicht so gut bestellt (eigentlich eher “grottenschlecht”):
glance(lm1)[1]| r.squared |
|---|
| 0.0025138 |
Die eckigen Klammern erlauben in R ein bestimmtes Element von mehreren auszuwählen. glance(lm1) liefert eine Tabelle mit mehreren Spalten (und einer Zeile) zurück; mit glance(lm1)[1] bekommt man das erste Element dieser Tabelle, das heißt die erste Spalte. Natürlich können Sie einfach glance(lm1) eingeben, wenn Sie das lieber mögen.
9 lm2: All in
# NICHT AUSFÜHREN
#lm2_all_in <- lm(dep_delay ~ ., data = flights_train2)Modell lm2_all_in ist hier keine gute Idee, da nominale Prädiktoren in Indikatorvariablen umgewandelt werden. Hat ein nominaler Prädiktor sehr viele Stufen (wie hier), so resultieren sehr viele Indikatorvariablen, was dem Regressionsmodell Probleme bereiten kann (bei mir hängt sich R auf). Besser ist es in dem Fall, die Anzahl der Stufen von nominalskalierten Variablen vorab zu begrenzen.
Bei kleineren Datensätzen (weniger Variablen, weniger Fälle) lohnt es sich aber oft, das “All-in-Modell” auszuprobieren, als Referenzmaßstab für andere Modelle.
10 flights_train3: Textvariablen in Faktorvariablen umwandeln
Begrenzen wir zunächst die Anzahl der Stufen der nominal skalierten Variablen:
flights_train3 <-
flights_train2 %>%
mutate(across(
.cols = where(is.character),
.fns = as.factor))Wem das across zu kompliziert ist, der kann auch alternativ (synonym) jede Variable einzeln in einen Faktor umwandeln und zwar so:
flights_train3a <-
flights_train2 %>%
mutate(tailnum = as.factor(tailnum),
origin = as.factor(origin),
dest = as.factor(dest),
carrier = as.factor(carrier)
)Das ist einfacher als mit across, aber dafür mehr Tipperei.
Wir müssen die Transformationen, die wir auf das Train-Sample anwenden, auch auf das Test-Sample anwenden:
10.1 flights_test3
flights_test3 <-
flights_test2 %>%
mutate(across(
.cols = where(is.character),
.fns = as.factor))flights_train3 %>%
select(where(is.factor)) %>%
names()
#> [1] "carrier" "tailnum" "origin" "dest"Z.B. dest hat viele Stufen:
flights_train3 %>%
count(dest, sort = TRUE)| dest | n |
|---|---|
| ORD | 12592 |
| ATL | 12573 |
| LAX | 12120 |
| BOS | 11311 |
| MCO | 10445 |
| CLT | 10275 |
| SFO | 9890 |
| FLL | 8866 |
| MIA | 8715 |
| DCA | 6872 |
| DTW | 6813 |
| DFW | 6325 |
| RDU | 5846 |
| TPA | 5544 |
| IAH | 5370 |
| DEN | 5300 |
| MSP | 5287 |
| PBI | 4849 |
| BNA | 4582 |
| LAS | 4504 |
| SJU | 4356 |
| IAD | 4029 |
| PHX | 3469 |
| BUF | 3422 |
| CLE | 3312 |
| STL | 3135 |
| MDW | 3057 |
| SEA | 2884 |
| CVG | 2792 |
| MSY | 2762 |
| RSW | 2648 |
| CMH | 2563 |
| PIT | 2103 |
| CHS | 2075 |
| SAN | 2069 |
| MKE | 2039 |
| JAX | 1952 |
| SLC | 1886 |
| BTV | 1873 |
| AUS | 1790 |
| RIC | 1760 |
| ROC | 1760 |
| PWM | 1733 |
| HOU | 1542 |
| IND | 1493 |
| MCI | 1420 |
| BWI | 1288 |
| MEM | 1275 |
| SYR | 1259 |
| PHL | 1180 |
| GSO | 1133 |
| ORF | 1091 |
| DAY | 1026 |
| PDX | 999 |
| SRQ | 887 |
| SDF | 843 |
| XNA | 765 |
| MHT | 689 |
| BQN | 653 |
| CAK | 639 |
| SNA | 621 |
| GSP | 618 |
| OMA | 587 |
| SAV | 565 |
| GRR | 549 |
| HNL | 549 |
| SAT | 504 |
| LGB | 499 |
| TYS | 436 |
| MSN | 400 |
| DSM | 398 |
| STT | 391 |
| BDL | 317 |
| ALB | 315 |
| BGR | 293 |
| PSE | 288 |
| BUR | 278 |
| OKC | 262 |
| PVD | 260 |
| SJC | 256 |
| TUL | 232 |
| SMF | 224 |
| OAK | 223 |
| BHM | 205 |
| ACK | 199 |
| ABQ | 196 |
| AVL | 175 |
| EGE | 165 |
| MVY | 152 |
| CRW | 105 |
| ILM | 78 |
| CAE | 74 |
| TVC | 72 |
| MYR | 42 |
| CHO | 31 |
| BZN | 23 |
| EYW | 14 |
| PSP | 14 |
| JAC | 12 |
| HDN | 11 |
| MTJ | 9 |
| SBN | 9 |
| ANC | 6 |
| LEX | 1 |
flights_train3 %>%
count(dest) %>%
ggplot() +
aes(y = fct_reorder(dest, n), x = n) +
geom_col()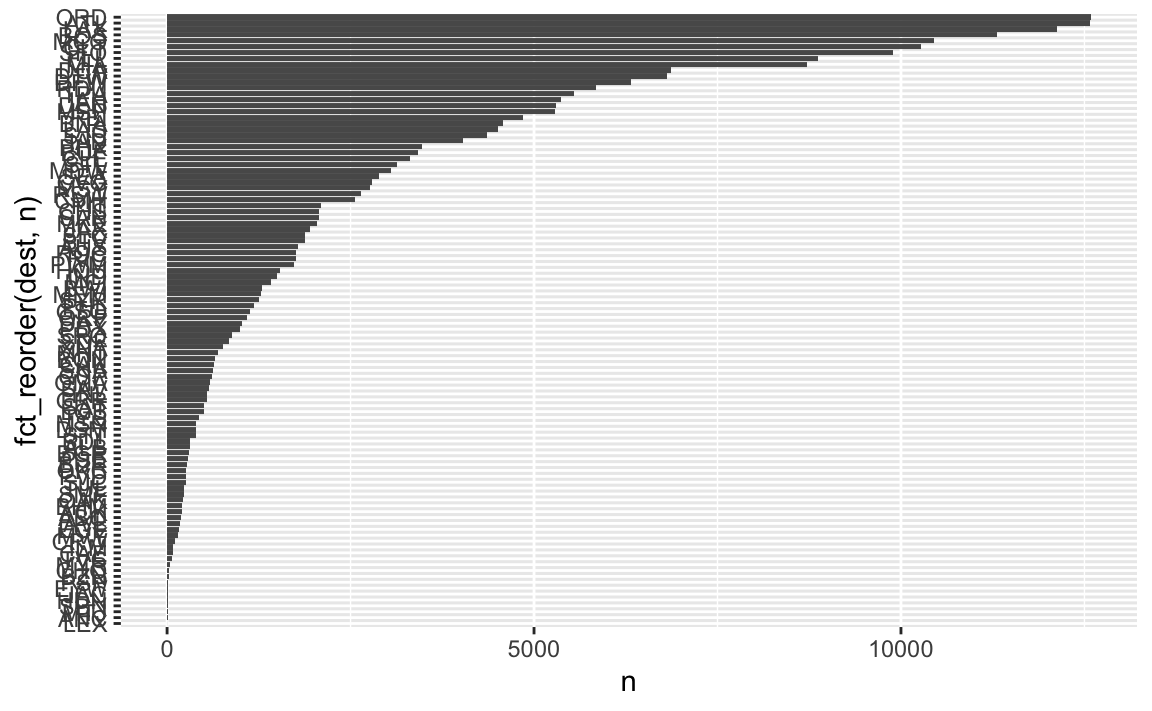
11 flights_train4: Faktorstufen zusammenfassen
flights_train4 <-
flights_train3 %>%
mutate(across(
.cols = where(is.factor),
.fns = fct_lump_prop, prop = .025
))flights_train4a <-
flights_train3 %>%
mutate(dest = fct_lump_prop(f = dest,
prop = .025))flights_train4a %>%
count(dest)| dest | n |
|---|---|
| ATL | 12573 |
| BOS | 11311 |
| CLT | 10275 |
| DCA | 6872 |
| DFW | 6325 |
| DTW | 6813 |
| FLL | 8866 |
| LAX | 12120 |
| MCO | 10445 |
| MIA | 8715 |
| ORD | 12592 |
| SFO | 9890 |
| Other | 129591 |
flights_train4 %>%
count(dest) %>%
ggplot() +
aes(y = fct_reorder(dest, n), x = n) +
geom_col()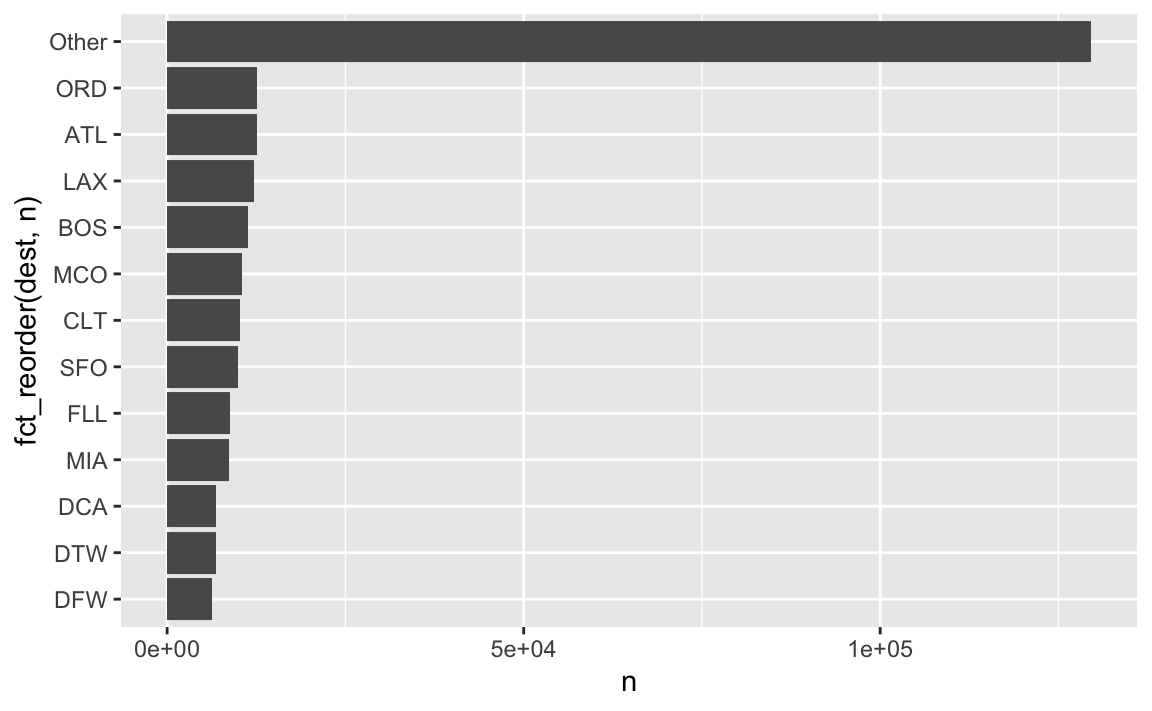
Check:
flights_train4 %>%
select(where(is.factor)) %>%
summarise(nlevels_dest = nlevels(dest))| nlevels_dest |
|---|
| 13 |
Oder alle Faktorvariablen auf einmal:
flights_train4 %>%
select(where(is.factor)) %>%
map_dfc(nlevels)| carrier | tailnum | origin | dest |
|---|---|---|---|
| 10 | 1 | 3 | 13 |
Das sind jetzt Zahlen von Faktorstufen, mit denen wir arbeiten können.
11.1 flights_test4
Vergessen wir nicht, die Transformation auch auf das Test-Sample anzuwenden:
flights_test4 <-
flights_test3 %>%
mutate(across(
.cols = where(is.factor),
.fns = fct_lump_prop, prop = .025
))12 lm3: Alle zusammengefassten Faktorvariablen
lm3 <- flights_train4 %>%
select(dep_delay, where(is.factor), -tailnum, -id) %>%
lm(dep_delay ~ ., data = .)Der Punkt bei dep_delay ~ . meint “nimm alle Variablen im Datensatz (bis auf dep_delay)”.
Der Punkt bei data = . nimm die Tabelle, wie sie dir im letzten Schritt mundgerecht aufbereitet wurde. Man hätte hier auch flights_train4 schreiben können, aber dann hätten wir noch tailnum etc. entfernen müssen.
Eigentlich brauchen wir nicht so viele Dezimalstellen …
options(digits = 2)glance zeigt das R-Quadrat (und einiges mehr, was hier jetzt nicht brauchen).
glance(lm3) # R^2| r.squared | adj.r.squared | sigma | statistic | p.value | df | logLik | AIC | BIC | deviance | df.residual | nobs |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0120133 | 0.0119211 | 39.90852 | 130.2453 | 0 | 23 | -1257929 | 2515908 | 2516168 | 392381512 | 246364 | 246388 |
tidy(lm3) # Modellkoeffizienten, also die Beta-Gewichte ("estimate")| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 18.6110801 | 0.5632182 | 33.044171 | 0.0000000 |
| carrierAA | -7.7840954 | 0.4917308 | -15.829994 | 0.0000000 |
| carrierB6 | -3.5670525 | 0.4116207 | -8.665873 | 0.0000000 |
| carrierDL | -7.0495136 | 0.4322994 | -16.307018 | 0.0000000 |
| carrierEV | 2.9860188 | 0.4598576 | 6.493356 | 0.0000000 |
| carrierMQ | -5.9204247 | 0.4724111 | -12.532356 | 0.0000000 |
| carrierUA | -4.9383977 | 0.4607246 | -10.718762 | 0.0000000 |
| carrierUS | -12.4725380 | 0.5694244 | -21.903765 | 0.0000000 |
| carrierWN | 1.4853670 | 0.5831405 | 2.547185 | 0.0108602 |
| carrierOther | -1.6794545 | 0.6073453 | -2.765238 | 0.0056885 |
| originJFK | -0.3188348 | 0.2827839 | -1.127486 | 0.2595383 |
| originLGA | -1.6386743 | 0.2444494 | -6.703531 | 0.0000000 |
| destBOS | -2.5196502 | 0.5619247 | -4.483964 | 0.0000073 |
| destCLT | -0.6733737 | 0.6234772 | -1.080029 | 0.2801302 |
| destDCA | -0.6758758 | 0.6672185 | -1.012975 | 0.3110730 |
| destDFW | -1.8925319 | 0.6953841 | -2.721563 | 0.0064978 |
| destDTW | -2.2827442 | 0.6088426 | -3.749317 | 0.0001774 |
| destFLL | -0.7902433 | 0.5797189 | -1.363149 | 0.1728368 |
| destLAX | -3.7037920 | 0.5541243 | -6.684046 | 0.0000000 |
| destMCO | -1.5642509 | 0.5531661 | -2.827814 | 0.0046871 |
| destMIA | -1.2900042 | 0.6062971 | -2.127677 | 0.0333649 |
| destORD | 1.5705786 | 0.5500706 | 2.855231 | 0.0043009 |
| destSFO | -0.7571220 | 0.5814538 | -1.302119 | 0.1928770 |
| destOther | -1.6264665 | 0.4091865 | -3.974878 | 0.0000704 |
Ein mageres R-Quadrat.
13 lm4: Alle metrischen Variablen
Was sind noch mal unsere metrischen Variablen:
flights_train4 %>%
select(where(is.numeric)) %>%
names()
#> [1] "id" "month" "day" "dep_time"
#> [5] "sched_dep_time" "dep_delay" "arr_time" "sched_arr_time"
#> [9] "flight" "air_time" "distance" "hour"
#> [13] "minute"Ok, jetzt eine Regression mit diesen Variablen (ober ohne die ID-Variable):
lm4 <-
flights_train4 %>%
select(dep_delay, where(is.numeric), -id) %>%
lm(dep_delay ~ ., data = .)glance(lm4)| r.squared | adj.r.squared | sigma | statistic | p.value | df | logLik | AIC | BIC | deviance | df.residual | nobs |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1381879 | 0.1381528 | 37.14452 | 3936.327 | 0 | 10 | -1235786 | 2471597 | 2471722 | 338706325 | 245490 | 245501 |
Tja, das \(R^2\) hat einen nicht gerade um …
14 lm5: Alle metrischen und alle (zusammengefassten) nominalen Variablen
Welche Variablen sind jetzt alle an Bord?
flights_train4 %>%
names()
#> [1] "id" "month" "day" "dep_time"
#> [5] "sched_dep_time" "dep_delay" "arr_time" "sched_arr_time"
#> [9] "carrier" "flight" "tailnum" "origin"
#> [13] "dest" "air_time" "distance" "hour"
#> [17] "minute" "time_hour"time_hour nehmen wir noch einmal raus, da es zum einen redundant ist zu hour etc. und zum anderen noch zusätzlicher Aufbereitung bedarf.
flights_train4 %>%
select(minute) %>%
skim()| Name | Piped data |
| Number of rows | 246388 |
| Number of columns | 1 |
| _______________________ | |
| Column type frequency: | |
| numeric | 1 |
| ________________________ | |
| Group variables | None |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| minute | 0 | 1 | 26.25 | 19.31 | 0 | 8 | 29 | 44 | 59 | ▇▃▆▃▅ |
lm5 <-
flights_train4 %>%
select(-time_hour, -tailnum, -id, -minute) %>% # "minute" machte Probleme, besser rausnehmen
lm(dep_delay ~ ., data = .)glance(lm5)| r.squared | adj.r.squared | sigma | statistic | p.value | df | logLik | AIC | BIC | deviance | df.residual | nobs |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1447169 | 0.1446019 | 37.00528 | 1258.602 | 0 | 33 | -1234853 | 2469776 | 2470140 | 336140327 | 245467 | 245501 |
Der Vorhersage-Gott ist nicht mit uns. Vielleicht sollten wir zu einem ehrlichen Metier als Schuhverkäufer umsatteln …
15 Wetter-Daten ergänzen
15.1 Wetterdaten laden
data("weather")glimpse(weather)
#> Rows: 26,115
#> Columns: 15
#> $ origin <chr> "EWR", "EWR", "EWR", "EWR", "EWR", "EWR", "EWR", "EWR", "EW…
#> $ year <int> 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2013,…
#> $ month <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
#> $ day <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
#> $ hour <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 18, …
#> $ temp <dbl> 39.02, 39.02, 39.02, 39.92, 39.02, 37.94, 39.02, 39.92, 39.…
#> $ dewp <dbl> 26.06, 26.96, 28.04, 28.04, 28.04, 28.04, 28.04, 28.04, 28.…
#> $ humid <dbl> 59.37, 61.63, 64.43, 62.21, 64.43, 67.21, 64.43, 62.21, 62.…
#> $ wind_dir <dbl> 270, 250, 240, 250, 260, 240, 240, 250, 260, 260, 260, 330,…
#> $ wind_speed <dbl> 10.35702, 8.05546, 11.50780, 12.65858, 12.65858, 11.50780, …
#> $ wind_gust <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 20.…
#> $ precip <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
#> $ pressure <dbl> 1012.0, 1012.3, 1012.5, 1012.2, 1011.9, 1012.4, 1012.2, 101…
#> $ visib <dbl> 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10,…
#> $ time_hour <dttm> 2013-01-01 01:00:00, 2013-01-01 02:00:00, 2013-01-01 03:00…skim(weather)| Name | weather |
| Number of rows | 26115 |
| Number of columns | 15 |
| _______________________ | |
| Column type frequency: | |
| character | 1 |
| numeric | 13 |
| POSIXct | 1 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| origin | 0 | 1 | 3 | 3 | 0 | 3 | 0 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| year | 0 | 1.00 | 2013.00 | 0.00 | 2013.00 | 2013.00 | 2013.00 | 2013.00 | 2013.00 | ▁▁▇▁▁ |
| month | 0 | 1.00 | 6.50 | 3.44 | 1.00 | 4.00 | 7.00 | 9.00 | 12.00 | ▇▆▆▆▇ |
| day | 0 | 1.00 | 15.68 | 8.76 | 1.00 | 8.00 | 16.00 | 23.00 | 31.00 | ▇▇▇▇▆ |
| hour | 0 | 1.00 | 11.49 | 6.91 | 0.00 | 6.00 | 11.00 | 17.00 | 23.00 | ▇▇▆▇▇ |
| temp | 1 | 1.00 | 55.26 | 17.79 | 10.94 | 39.92 | 55.40 | 69.98 | 100.04 | ▂▇▇▇▁ |
| dewp | 1 | 1.00 | 41.44 | 19.39 | -9.94 | 26.06 | 42.08 | 57.92 | 78.08 | ▁▆▇▇▆ |
| humid | 1 | 1.00 | 62.53 | 19.40 | 12.74 | 47.05 | 61.79 | 78.79 | 100.00 | ▁▆▇▇▆ |
| wind_dir | 460 | 0.98 | 199.76 | 107.31 | 0.00 | 120.00 | 220.00 | 290.00 | 360.00 | ▆▂▆▇▇ |
| wind_speed | 4 | 1.00 | 10.52 | 8.54 | 0.00 | 6.90 | 10.36 | 13.81 | 1048.36 | ▇▁▁▁▁ |
| wind_gust | 20778 | 0.20 | 25.49 | 5.95 | 16.11 | 20.71 | 24.17 | 28.77 | 66.75 | ▇▅▁▁▁ |
| precip | 0 | 1.00 | 0.00 | 0.03 | 0.00 | 0.00 | 0.00 | 0.00 | 1.21 | ▇▁▁▁▁ |
| pressure | 2729 | 0.90 | 1017.90 | 7.42 | 983.80 | 1012.90 | 1017.60 | 1023.00 | 1042.10 | ▁▁▇▆▁ |
| visib | 0 | 1.00 | 9.26 | 2.06 | 0.00 | 10.00 | 10.00 | 10.00 | 10.00 | ▁▁▁▁▇ |
Variable type: POSIXct
| skim_variable | n_missing | complete_rate | min | max | median | n_unique |
|---|---|---|---|---|---|---|
| time_hour | 0 | 1 | 2013-01-01 01:00:00 | 2013-12-30 18:00:00 | 2013-07-01 14:00:00 | 8714 |
wind_gust hat zu viele fehlende Werte; diese Variable dürfen wir nicht verwenden.
15.2 flights_train5: Wetterdaten mit Flugdaten verheiraten
flights_train5 <-
flights_train4 %>%
left_join(weather) %>% # "verheiraten"
select(-wind_gust)Möchte man explizit angeben, anhand welcher Variablen man zusammenfügen möchte, so kann man dies mit dem Parameter by tun:
by = c("origin", "month" , "day", "hour")Unter der Hilfeseite von left_join findet man mehr Infos: ?left_join.
flights_test5 <-
flights_test4 %>%
left_join(weather) %>%
select(-wind_gust)16 flights_train6
Bei der Gelegenheit löschen wir noch zwei Variablen, die wir bisher nicht benötigt haben.
flights_train6 <-
flights_train5 %>%
select(-time_hour, -tailnum, -minute)flights_test6 <-
flights_test5 %>%
select(-time_hour, -tailnum, -minute)17 lm6: Plus Wetterdaten
lm6 <- update(lm5, . ~ . + humid + wind_speed + precip + pressure + visib,
data = flights_train6)glance(lm6)| r.squared | adj.r.squared | sigma | statistic | p.value | df | logLik | AIC | BIC | deviance | df.residual | nobs |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1620316 | 0.1618858 | 34.26088 | 1110.918 | 0 | 38 | -1081500 | 2163080 | 2163492 | 256265775 | 218320 | 218359 |
Ah. Etwas besser. Wettervorhersage macht’s möglich.
\(R^2\) kann man auch so berechnen:
flights_train6_pred <-
flights_train6 %>%
mutate(lm6_pred = predict(lm6, newdata = .))
flights_train6_pred %>%
rsq(truth = dep_delay,
estimate = lm6_pred)| .metric | .estimator | .estimate |
|---|---|---|
| rsq | standard | 0.1620316 |
17.1 R2 im Testsample
Berechnen wir jetzt die Modellgüte im Testsample.
Fügen wir die Vorhersagewerte dem Testsample dazu:
flights_test6_pred <-
flights_test6 %>%
mutate(pred_lm6 = predict(lm6, newdata = flights_test6))flights_test6_pred %>%
select(id, dep_delay, pred_lm6) %>%
head()| id | dep_delay | pred_lm6 |
|---|---|---|
| 1 | 2 | 0.3247318 |
| 2 | 4 | -1.4677357 |
| 11 | -2 | -0.1192573 |
| 19 | 0 | 1.6611710 |
| 30 | 0 | 4.2525720 |
| 49 | -2 | 2.6402972 |
test_rsq <-
tibble(model = "lm6") %>%
mutate(rsq = rsq_vec(truth = flights_test6_pred$dep_delay,
estimate = flights_test6_pred$pred_lm6))
test_rsq| model | rsq |
|---|---|
| lm6 | 0.1534751 |
Prüfen wir noch, wie viele fehlende Werte es bei den vorhergesagten Werten gibt:
flights_test6_pred %>%
summarise(pred_isna = sum(is.na(pred_lm6)),
pred_isna_prop = pred_isna / nrow(flights_test6_pred)) # prop wie "proportion" (Anteil)| pred_isna | pred_isna_prop |
|---|---|
| 9352 | 0.1138641 |
Da fehlende Werte u.U. mit dem Mittelwert (der übrigen prognostizierten Werte) aufgefüllt werden, erledigen wir das gleich, um den Effekt auf \(R^2\) abzuschätzen:
flights_test6_pred2 <-
flights_test6_pred %>%
mutate(pred_lm6 = replace_na(pred_lm6, mean(pred_lm6, na.rm = TRUE)))flights_test6_pred2 %>%
summarise(sum(is.na(pred_lm6)))| sum(is.na(pred_lm6)) |
|---|
| 0 |
Keine fehlenden Werte mehr.
Wie sieht \(R^2\) jetzt aus?
flights_test6_pred2 %>%
rsq(truth = dep_delay, estimate = pred_lm6)| .metric | .estimator | .estimate |
|---|---|---|
| rsq | standard | 0.1204287 |
Etwas schlechter; das liegt an den vielen Werten, die jetzt eine schlechte Vorhersage machen, da sie mit dem Mittelwert aufgefüllt werden mussten.
18 lm7: Rohe Gewalt
Wir könnten einfach, etwas stumpfsinnig, alle Regressionsmodelle ausprobieren: Jeder der \(p\) Prädiktoren könnte also entweder enthalten sein oder nicht. Natürlich würde das schnell zu Arbeit auswachsen, wenn man so viele Regressionsmodelle – \(2^p\) – durchprobieren würde. Außerdem wird die Gefahr von Zufallsbefunden schnell riesig. Aber gut, man kann stumpfsinnige Arbeiten ja gut an den Computer delegieren. Und zum Schutz vor Überanpassung gibt es ein paar Behelfe. Probieren wir es aus; dazu nutzen wir das Paket {leaps}.
tic() # Zeitmessung t1
lm7 <- regsubsets(dep_delay ~ .,
nvmax = 15, # max. Anzahl von Prädiktoren
data = flights_train6)
#> Reordering variables and trying again:
toc() # Zeitmessung t2
#> 41.618 sec elapsedDer Punkt in der Regressionsformel
dep_delay ~ .,
bedeutet “nimm alle übrigen Variablen” (also alle außer der abhängigen Variablen).
Je größer nvmax, desto länger die Rechenzeit, z.B. \(2^{15}=32768\) Modelle, die berechnet werden müssen.
Achtung: Einige Statistiker (siehe auch hier) stehen solchen automatischen Verfahren kritisch gegenüber, sind also der Meinung, das sei Quatsch (andere wiederum nutzen diese Verfahren).
18.1 Zeitabschätzung
Ein kurze Sch+ätzung der Rechenzeit in Abhängikeit der Anzahl der Prädiktoren bei der Best-Subset-Methode; gehen wir von 1, 2 oder 5 Sekunden Rechenzeit (exec_time) pro Modell aus.
n_preds <- 1:20
exec_time <- c(1, 2, 5)exec_time_df <-
expand_grid(n_preds = n_preds,
exec_time_per_run = exec_time)exec_time_df <-
exec_time_df %>%
mutate(exec_time = 2^n_preds * exec_time_per_run) %>%
group_by(exec_time_per_run) %>%
mutate(exec_time_cum = cumsum(exec_time) / 60 / 60 / 60)head(exec_time_df)
#> # A tibble: 6 x 4
#> # Groups: exec_time_per_run [3]
#> n_preds exec_time_per_run exec_time exec_time_cum
#> <int> <dbl> <dbl> <dbl>
#> 1 1 1 2 0.00000926
#> 2 1 2 4 0.0000185
#> 3 1 5 10 0.0000463
#> 4 2 1 4 0.0000278
#> 5 2 2 8 0.0000556
#> 6 2 5 20 0.000139exec_time_df %>%
ggplot() +
aes(x = n_preds,
y = exec_time_cum,
color = factor(exec_time_per_run)) +
geom_line() +
labs(y = "GesamtRechenzeit in Stunden",
x = "Anzahl von Prädiktoren pro Modell",
col = "Rechenzeit pro Modell",
title = "Schätzung der Rechenzeit für eine Best-Subset-Regression") +
theme(legend.position = "bottom")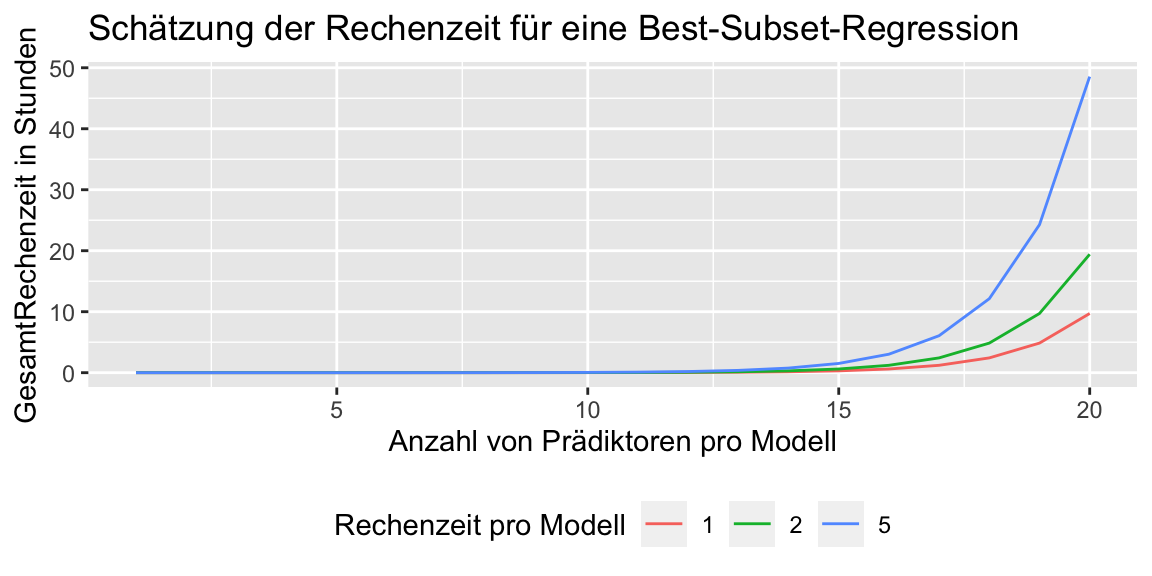
Puh, das kann dauern, wenn man viele Prädiktoren hat.
18.2 Best Subsets – Ergebnisse
Schauen wir uns die Ergebnisse an:
lm7_summary <- summary(lm7)
tibble(adjr2 = lm7_summary$adjr2,
r2 = lm7_summary$rsq,
bic = lm7_summary$bic,
id = 1:length(lm7_summary$adjr2)) %>%
pivot_longer(-id) %>%
ggplot() +
aes(x = id, y = value, color = name) +
geom_point() +
geom_line() +
facet_wrap(~ name, scales = "free", nrow = 3) +
scale_x_continuous(breaks = 1:16)
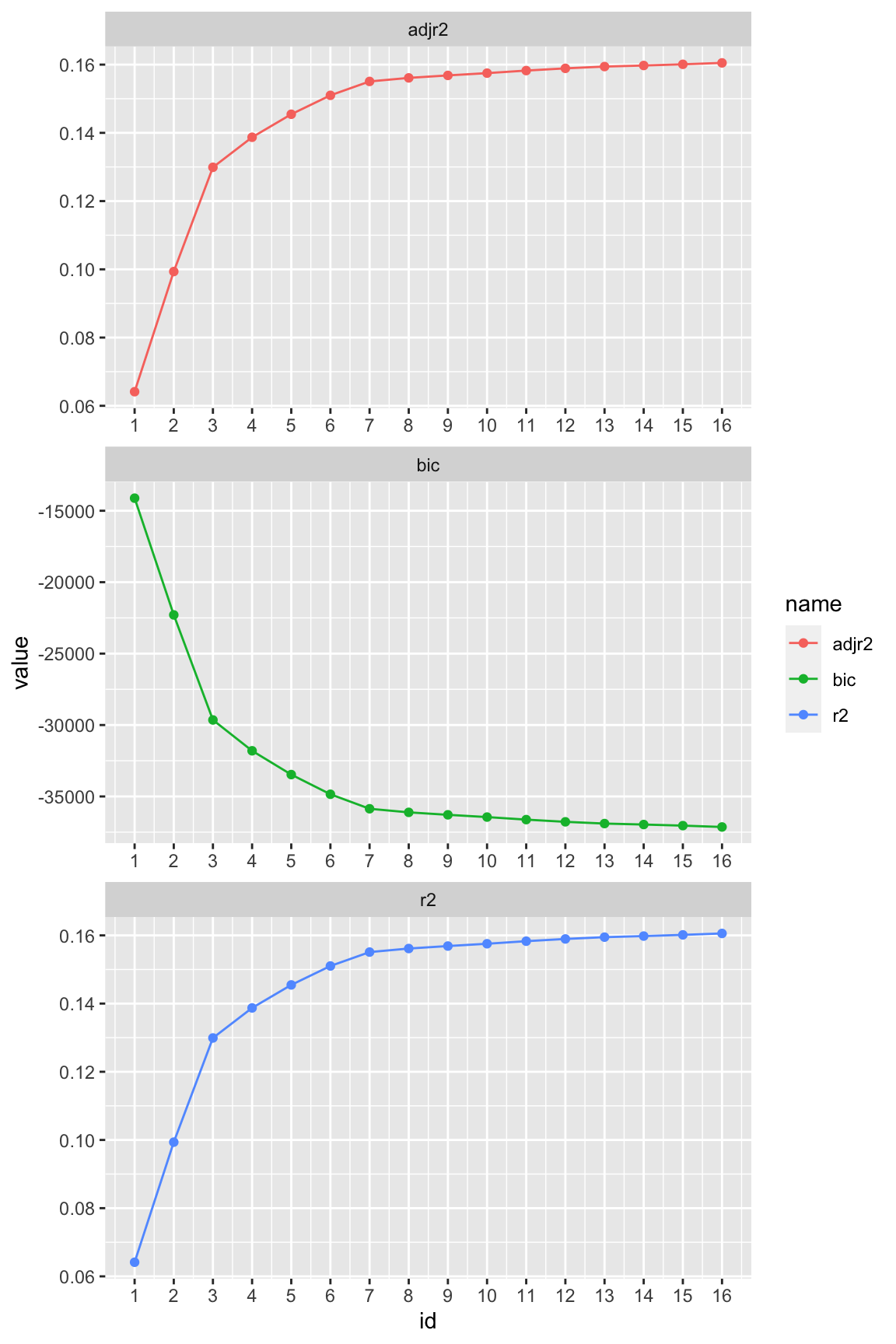
Das Modell mit 7 Prädiktoren könnte sinnvoll sein. Mit coef(modellname, k) können wir uns ausgeben lassen, welche Prädiktoren in dem Modell mit k Prädiktoren beinhaltet waren.
coef(lm7, 7) %>% names()
#> [1] "(Intercept)" "dep_time" "sched_dep_time" "arr_time"
#> [5] "sched_arr_time" "carrierEV" "wind_dir" "visib"18.3 Vorwärts-/Rückwärts-Schrittweise Regression
Man kann regsubsets übrigens auch für eine schrittweise Regression benutzen:
lm7a <- regsubsets(dep_delay ~ .,
method = "forward", # Vorwärts-Schrittweise-Regression
nvmax = 15, # max. Anzahl von Prädiktoren
data = flights_train6)
#> Reordering variables and trying again:Das Modell mit einem Prädiktor findet das folgende Modell als das beste:
coef(lm7a, 1)
#> (Intercept) dep_time
#> -15.31028825 0.01944815Und entsprechend:
coef(lm7a, 2)
#> (Intercept) dep_time arr_time
#> -6.10576901 0.03280038 -0.01805599Und so weiter für 3, 4 oder mehr Prädiktoren.
Im Unterschied zur Best-Subsets-Methode verbleiben Prädiktoren, wenn einmal aufgenommen ins Modell, immer im Modell.
Die Schrittweise-Regression ist weniger rechenintiv, da weniger Modelle berechnet werden müssen und kann daher u.U. das beste Modell übersehen.
Beide Verfahren der automatisierten Prädiktorenauswahl – Best-Subset und Schrittweise-Regression – werden von einigen Statistikern kritisch gesehen.
19 lm8: Bestes Modell aus der Best-Subset-Analyse
flights_train7 <-
flights_train6 %>%
mutate(carrierEV = fct_other(carrier,
keep = "EV")) flights_test7 <-
flights_test6 %>%
mutate(carrierEV = fct_other(carrier,
keep = "EV")) lm8 <-
lm(dep_delay ~ dep_time + sched_dep_time + arr_time + carrierEV + wind_dir + sched_arr_time + visib,
data = flights_train7)
glance(lm8)| r.squared | adj.r.squared | sigma | statistic | p.value | df | logLik | AIC | BIC | deviance | df.residual | nobs |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1499841 | 0.1499592 | 36.90093 | 6018.739 | 0 | 7 | -1200390 | 2400798 | 2400891 | 325132132 | 238773 | 238781 |
Hm; nicht so gut.
19.1 R2 im Testdatensatz
flights_test7_pred <-
flights_test7 %>%
mutate(pred_lm8 = predict(lm8, newdata = flights_test7)) %>%
select(id, dep_delay, pred_lm8)test_rsq <-
test_rsq %>%
bind_rows(tibble(
model = "lm8",
rsq = rsq_vec(truth = flights_test7_pred$dep_delay,
estimate = flights_test7_pred$pred_lm8)))
test_rsq| model | rsq |
|---|---|
| lm6 | 0.1534751 |
| lm8 | 0.1396282 |
Ein typischer Befund bei Regressionsanalysen (ohne Polynome): Im Testdatensatz ist \(R^2\) etwas geringer als im Train-Datensatz. Bei Modellen mit Polynomen oder anderen flexiblen Modellen kann der Unterschied zwischen Train- und Test-Sample noch viel größer sein.
20 Prüfen der Modellqualität
autoplot(lm6, which = 1)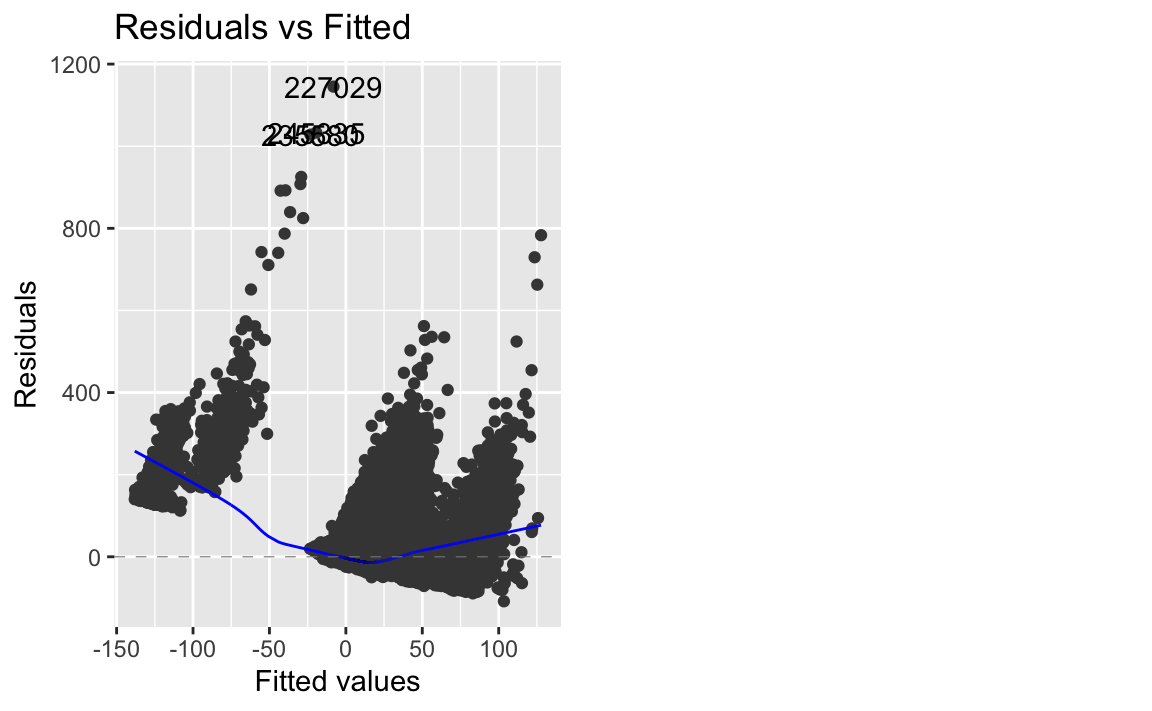
Abweichungen von der Linearität finden sich besonders bei sehr kleinen und sehr großen Werten; das ist ein Hinweise, dass unser Modell nicht-lineare Zusammenhänge nicht erkannt. Das ist kein Wunder, schließlich besteht unser Modell nur aus linearen Termen. Interaktionen, Polynome oder logarithmische Transformationen könnten das Modell verbessern und eröffnen Raum für weitere Analysen.
21 Einreichen
Das beste Modell im Trainsample reichen wir ein; in diesem Fall lm6. Wenn die Maßgabe ist, für alle Fälle des Datensatzes eine Vorhersage einzureichen, tun wir das natürlich:
flights6 <-
flights_train6 %>%
bind_rows(flights_test6) flights6_pred <-
flights6 %>%
mutate(pred = predict(lm6, newdata = .)) %>%
select(id, pred)head(flights6_pred)| id | pred |
|---|---|
| 5 | -0.1549456 |
| 7 | 0.8112611 |
| 21 | -1.7284946 |
| 31 | -4.1875960 |
| 34 | 6.2202257 |
| 35 | -1.1899645 |
Wie viele vorhergesagte Werte haben wir, bzw. welchen Anteil?
flights6_pred %>%
drop_na() %>%
nrow() / nrow(flights6_pred)
#> [1] 0.886214321.1 CSV-Datei erstellen zum Einreichen
write_csv(flights6_pred, file = "Sauer_Sebastian_0123456_Prognose.csv")22 Was noch?
Ein nächster Schritt könnte sein, sich folgende Punkte anzuschauen:
- Interaktionen
- Polynome
- Voraussetzungen
Eine Faustregel zu Interaktionen lautet: Wenn zwei Variablen jeweils einen starken Haupteffekt haben, lohnt es sich u.U., den Interaktionseffekt anzuschauen (vgl. Gelman & Hill, 2007, S. 69).
23 Tidymodels
Das ständige Updaten des Test-Datensatzes nervt; mit tidymodels wird es komfortabler und man hat Zugang zu leistungsfähigeren Prognosemodellen. Hier findet sich ein Einstieg und hier eine Fallstudie mit Tutorial.
24 Reproducibility
#> ─ Session info ───────────────────────────────────────────────────────────────────────────────────────────────────────
#> setting value
#> version R version 4.1.0 (2021-05-18)
#> os macOS Big Sur 10.16
#> system x86_64, darwin17.0
#> ui X11
#> language (EN)
#> collate en_US.UTF-8
#> ctype en_US.UTF-8
#> tz Europe/Berlin
#> date 2021-06-24
#>
#> ─ Packages ───────────────────────────────────────────────────────────────────────────────────────────────────────────
#> package * version date lib source
#> assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.1.0)
#> backports 1.2.1 2020-12-09 [1] CRAN (R 4.1.0)
#> base64enc 0.1-3 2015-07-28 [1] CRAN (R 4.1.0)
#> blogdown 1.3 2021-04-14 [2] CRAN (R 4.1.0)
#> bookdown 0.22 2021-04-22 [2] CRAN (R 4.1.0)
#> broom * 0.7.6 2021-04-05 [1] CRAN (R 4.1.0)
#> bslib 0.2.5.1 2021-05-18 [1] CRAN (R 4.1.0)
#> cachem 1.0.5 2021-05-15 [2] CRAN (R 4.1.0)
#> callr 3.7.0 2021-04-20 [1] CRAN (R 4.1.0)
#> cellranger 1.1.0 2016-07-27 [1] CRAN (R 4.1.0)
#> class 7.3-19 2021-05-03 [2] CRAN (R 4.1.0)
#> cli 2.5.0 2021-04-26 [1] CRAN (R 4.1.0)
#> codetools 0.2-18 2020-11-04 [2] CRAN (R 4.1.0)
#> colorspace 2.0-1 2021-05-04 [1] CRAN (R 4.1.0)
#> conflicted * 1.0.4 2019-06-21 [1] CRAN (R 4.1.0)
#> crayon 1.4.1 2021-02-08 [1] CRAN (R 4.1.0)
#> DBI 1.1.1 2021-01-15 [1] CRAN (R 4.1.0)
#> dbplyr 2.1.1 2021-04-06 [1] CRAN (R 4.1.0)
#> desc 1.3.0 2021-03-05 [2] CRAN (R 4.1.0)
#> devtools 2.4.1 2021-05-05 [2] CRAN (R 4.1.0)
#> dials * 0.0.9 2020-09-16 [1] CRAN (R 4.1.0)
#> DiceDesign 1.9 2021-02-13 [1] CRAN (R 4.1.0)
#> digest 0.6.27 2020-10-24 [1] CRAN (R 4.1.0)
#> dplyr * 1.0.6 2021-05-05 [1] CRAN (R 4.1.0)
#> ellipsis 0.3.2 2021-04-29 [1] CRAN (R 4.1.0)
#> evaluate 0.14 2019-05-28 [1] CRAN (R 4.1.0)
#> fansi 0.5.0 2021-05-25 [1] CRAN (R 4.1.0)
#> farver 2.1.0 2021-02-28 [1] CRAN (R 4.1.0)
#> fastmap 1.1.0 2021-01-25 [2] CRAN (R 4.1.0)
#> forcats * 0.5.1 2021-01-27 [1] CRAN (R 4.1.0)
#> foreach 1.5.1 2020-10-15 [2] CRAN (R 4.1.0)
#> fs 1.5.0 2020-07-31 [1] CRAN (R 4.1.0)
#> furrr 0.2.2 2021-01-29 [1] CRAN (R 4.1.0)
#> future 1.21.0 2020-12-10 [1] CRAN (R 4.1.0)
#> generics 0.1.0 2020-10-31 [1] CRAN (R 4.1.0)
#> ggfortify * 0.4.11 2020-10-02 [2] CRAN (R 4.1.0)
#> ggplot2 * 3.3.4 2021-06-16 [1] CRAN (R 4.1.0)
#> globals 0.14.0 2020-11-22 [1] CRAN (R 4.1.0)
#> glue 1.4.2 2020-08-27 [1] CRAN (R 4.1.0)
#> gower 0.2.2 2020-06-23 [1] CRAN (R 4.1.0)
#> GPfit 1.0-8 2019-02-08 [1] CRAN (R 4.1.0)
#> gridExtra 2.3 2017-09-09 [2] CRAN (R 4.1.0)
#> gtable 0.3.0 2019-03-25 [1] CRAN (R 4.1.0)
#> haven 2.4.1 2021-04-23 [1] CRAN (R 4.1.0)
#> highr 0.9 2021-04-16 [1] CRAN (R 4.1.0)
#> hms 1.1.0 2021-05-17 [1] CRAN (R 4.1.0)
#> htmltools 0.5.1.1 2021-01-22 [1] CRAN (R 4.1.0)
#> httr 1.4.2 2020-07-20 [1] CRAN (R 4.1.0)
#> infer * 0.5.4 2021-01-13 [1] CRAN (R 4.1.0)
#> ipred 0.9-11 2021-03-12 [1] CRAN (R 4.1.0)
#> iterators 1.0.13 2020-10-15 [2] CRAN (R 4.1.0)
#> jquerylib 0.1.4 2021-04-26 [1] CRAN (R 4.1.0)
#> jsonlite 1.7.2 2020-12-09 [1] CRAN (R 4.1.0)
#> knitr 1.33 2021-04-24 [1] CRAN (R 4.1.0)
#> labeling 0.4.2 2020-10-20 [1] CRAN (R 4.1.0)
#> lattice 0.20-44 2021-05-02 [2] CRAN (R 4.1.0)
#> lava 1.6.9 2021-03-11 [1] CRAN (R 4.1.0)
#> leaps * 3.1 2020-01-16 [1] CRAN (R 4.1.0)
#> lhs 1.1.1 2020-10-05 [1] CRAN (R 4.1.0)
#> lifecycle 1.0.0 2021-02-15 [1] CRAN (R 4.1.0)
#> listenv 0.8.0 2019-12-05 [1] CRAN (R 4.1.0)
#> lubridate 1.7.10 2021-02-26 [1] CRAN (R 4.1.0)
#> magrittr 2.0.1 2020-11-17 [1] CRAN (R 4.1.0)
#> MASS 7.3-54 2021-05-03 [2] CRAN (R 4.1.0)
#> Matrix 1.3-4 2021-06-01 [2] CRAN (R 4.1.0)
#> memoise 2.0.0 2021-01-26 [2] CRAN (R 4.1.0)
#> modeldata * 0.1.0 2020-10-22 [1] CRAN (R 4.1.0)
#> modelr 0.1.8 2020-05-19 [1] CRAN (R 4.1.0)
#> munsell 0.5.0 2018-06-12 [1] CRAN (R 4.1.0)
#> nnet 7.3-16 2021-05-03 [2] CRAN (R 4.1.0)
#> nycflights13 * 1.0.2 2021-04-12 [1] CRAN (R 4.1.0)
#> parallelly 1.25.0 2021-04-30 [1] CRAN (R 4.1.0)
#> parsnip * 0.1.6 2021-05-27 [1] CRAN (R 4.1.0)
#> pillar 1.6.1 2021-05-16 [1] CRAN (R 4.1.0)
#> pkgbuild 1.2.0 2020-12-15 [2] CRAN (R 4.1.0)
#> pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.1.0)
#> pkgload 1.2.1 2021-04-06 [2] CRAN (R 4.1.0)
#> plyr 1.8.6 2020-03-03 [1] CRAN (R 4.1.0)
#> prettyunits 1.1.1 2020-01-24 [1] CRAN (R 4.1.0)
#> printr * 0.1.1 2021-01-27 [1] CRAN (R 4.1.0)
#> pROC 1.17.0.1 2021-01-13 [1] CRAN (R 4.1.0)
#> processx 3.5.2 2021-04-30 [1] CRAN (R 4.1.0)
#> prodlim 2019.11.13 2019-11-17 [1] CRAN (R 4.1.0)
#> ps 1.6.0 2021-02-28 [1] CRAN (R 4.1.0)
#> purrr * 0.3.4 2020-04-17 [1] CRAN (R 4.1.0)
#> R6 2.5.0 2020-10-28 [1] CRAN (R 4.1.0)
#> Rcpp 1.0.6 2021-01-15 [1] CRAN (R 4.1.0)
#> readr * 1.4.0 2020-10-05 [1] CRAN (R 4.1.0)
#> readxl 1.3.1 2019-03-13 [1] CRAN (R 4.1.0)
#> recipes * 0.1.16 2021-04-16 [1] CRAN (R 4.1.0)
#> remotes 2.4.0 2021-06-02 [2] CRAN (R 4.1.0)
#> repr 1.1.3 2021-01-21 [1] CRAN (R 4.1.0)
#> reprex 2.0.0 2021-04-02 [1] CRAN (R 4.1.0)
#> rlang 0.4.11 2021-04-30 [1] CRAN (R 4.1.0)
#> rmarkdown 2.8 2021-05-07 [1] CRAN (R 4.1.0)
#> rpart 4.1-15 2019-04-12 [2] CRAN (R 4.1.0)
#> rprojroot 2.0.2 2020-11-15 [2] CRAN (R 4.1.0)
#> rsample * 0.1.0 2021-05-08 [1] CRAN (R 4.1.0)
#> rstudioapi 0.13 2020-11-12 [1] CRAN (R 4.1.0)
#> rvest 1.0.0 2021-03-09 [1] CRAN (R 4.1.0)
#> sass 0.4.0 2021-05-12 [1] CRAN (R 4.1.0)
#> scales * 1.1.1 2020-05-11 [1] CRAN (R 4.1.0)
#> sessioninfo 1.1.1 2018-11-05 [2] CRAN (R 4.1.0)
#> skimr * 2.1.3 2021-03-07 [1] CRAN (R 4.1.0)
#> stringi 1.6.2 2021-05-17 [1] CRAN (R 4.1.0)
#> stringr * 1.4.0 2019-02-10 [1] CRAN (R 4.1.0)
#> survival 3.2-11 2021-04-26 [2] CRAN (R 4.1.0)
#> testthat 3.0.2 2021-02-14 [2] CRAN (R 4.1.0)
#> tibble * 3.1.2 2021-05-16 [1] CRAN (R 4.1.0)
#> tidymodels * 0.1.3 2021-04-19 [1] CRAN (R 4.1.0)
#> tidyr * 1.1.3 2021-03-03 [1] CRAN (R 4.1.0)
#> tidyselect 1.1.1 2021-04-30 [1] CRAN (R 4.1.0)
#> tidyverse * 1.3.1 2021-04-15 [1] CRAN (R 4.1.0)
#> timeDate 3043.102 2018-02-21 [1] CRAN (R 4.1.0)
#> tune * 0.1.5 2021-04-23 [1] CRAN (R 4.1.0)
#> usethis 2.0.1 2021-02-10 [2] CRAN (R 4.1.0)
#> utf8 1.2.1 2021-03-12 [1] CRAN (R 4.1.0)
#> vctrs 0.3.8 2021-04-29 [1] CRAN (R 4.1.0)
#> withr 2.4.2 2021-04-18 [1] CRAN (R 4.1.0)
#> workflows * 0.2.2 2021-03-10 [1] CRAN (R 4.1.0)
#> workflowsets * 0.0.2 2021-04-16 [1] CRAN (R 4.1.0)
#> xfun 0.23 2021-05-15 [1] CRAN (R 4.1.0)
#> xml2 1.3.2 2020-04-23 [1] CRAN (R 4.1.0)
#> yaml 2.2.1.99 2021-06-18 [1] Github (viking/r-yaml@4788abe)
#> yardstick * 0.0.8 2021-03-28 [1] CRAN (R 4.1.0)
#>
#> [1] /Users/sebastiansaueruser/Library/R/x86_64/4.1/library
#> [2] /Library/Frameworks/R.framework/Versions/4.1/Resources/library