- 1 Pakete laden
- 2 Hintergrund und Ziel
- 3 Daten laden
- 4 Was ist Verspätung?
- 5 Verteilung der Verspätung
- 6 Deskriptive Statistiken
- 7 Korrelate von Verspätung
- 8 Fazit
- 9 Achtung
- 10 Reproduzierbarkeit
1 Pakete laden
library(tidyverse) # data wrangling
library(fastDummies) # nur für "Dummyisierung"
library(skimr) # viele Statistiken auf einmal
library(corrr) # komfortabel Korrelationen ausrechnen2 Hintergrund und Ziel
Dieser Post zeigt einige mögliche/typische Schritte der explorativen Datenanalyse (EDA) im Hinblick auf die Forschungsfrage “Welche Variablen steht in Zusammenhang mit Flugverspätungen?”.
3 Daten laden
Der Datensatz kann z.B. hier bezogen werden:
flights <- read_csv("https://vincentarelbundock.github.io/Rdatasets/csv/nycflights13/flights.csv")Der Datensatz ist relativ groß:
dim(flights)
#> [1] 336776 20Alternativ findet man den Datensatz auch im Paket nycflights13.
data(flights, package = "nycflights13")4 Was ist Verspätung?
Schauen wir uns den Datensatz mal näher an, um die Zielvariable “Verspätung” zu beleuchten.
glimpse(flights)
#> Rows: 336,776
#> Columns: 20
#> $ X1 <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, …
#> $ year <dbl> 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2…
#> $ month <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
#> $ day <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
#> $ dep_time <dbl> 517, 533, 542, 544, 554, 554, 555, 557, 557, 558, 558, …
#> $ sched_dep_time <dbl> 515, 529, 540, 545, 600, 558, 600, 600, 600, 600, 600, …
#> $ dep_delay <dbl> 2, 4, 2, -1, -6, -4, -5, -3, -3, -2, -2, -2, -2, -2, -1…
#> $ arr_time <dbl> 830, 850, 923, 1004, 812, 740, 913, 709, 838, 753, 849,…
#> $ sched_arr_time <dbl> 819, 830, 850, 1022, 837, 728, 854, 723, 846, 745, 851,…
#> $ arr_delay <dbl> 11, 20, 33, -18, -25, 12, 19, -14, -8, 8, -2, -3, 7, -1…
#> $ carrier <chr> "UA", "UA", "AA", "B6", "DL", "UA", "B6", "EV", "B6", "…
#> $ flight <dbl> 1545, 1714, 1141, 725, 461, 1696, 507, 5708, 79, 301, 4…
#> $ tailnum <chr> "N14228", "N24211", "N619AA", "N804JB", "N668DN", "N394…
#> $ origin <chr> "EWR", "LGA", "JFK", "JFK", "LGA", "EWR", "EWR", "LGA",…
#> $ dest <chr> "IAH", "IAH", "MIA", "BQN", "ATL", "ORD", "FLL", "IAD",…
#> $ air_time <dbl> 227, 227, 160, 183, 116, 150, 158, 53, 140, 138, 149, 1…
#> $ distance <dbl> 1400, 1416, 1089, 1576, 762, 719, 1065, 229, 944, 733, …
#> $ hour <dbl> 5, 5, 5, 5, 6, 5, 6, 6, 6, 6, 6, 6, 6, 6, 6, 5, 6, 6, 6…
#> $ minute <dbl> 15, 29, 40, 45, 0, 58, 0, 0, 0, 0, 0, 0, 0, 0, 0, 59, 0…
#> $ time_hour <dttm> 2013-01-01 05:00:00, 2013-01-01 05:00:00, 2013-01-01 0…Es gibt zwei Spalten, die auf Verspätung hinzielen:
flights %>%
select(contains("delay")) %>%
head()| dep_delay | arr_delay |
|---|---|
| 2 | 11 |
| 4 | 20 |
| 2 | 33 |
| -1 | -18 |
| -6 | -25 |
| -4 | 12 |
Ein Blick in die Hilfe lässt uns mehr lernen, was die Spalten bedeuten: help(flights) (wenn das Paket nycflights13 geladen ist; alternativ kann man z.B. hier nachlesen):
dep_delay, arr_delay
Departure and arrival delays, in minutes.
Negative times represent early departures/arrivals.4.1 Wie ähnlich sind Ankunfts- und Abflugsverspätung?
Da der Datensatz so groß ist, ziehen wir eine Stichprobe, dann geht alles schneller. Hier nicht wichtig, nur um etwas Zeit beim Plotten zu sparen. In der Praxis würde ich in an dieser Stelle keine Stichprobe ziehen, bzw. mit dem Gesamtdatensatz weiterarbeiten (was wir ja auch im Folgenden tun).
flights %>%
sample_n(size = 1000) %>%
ggplot() +
aes(y = dep_delay, x = arr_delay) +
geom_point()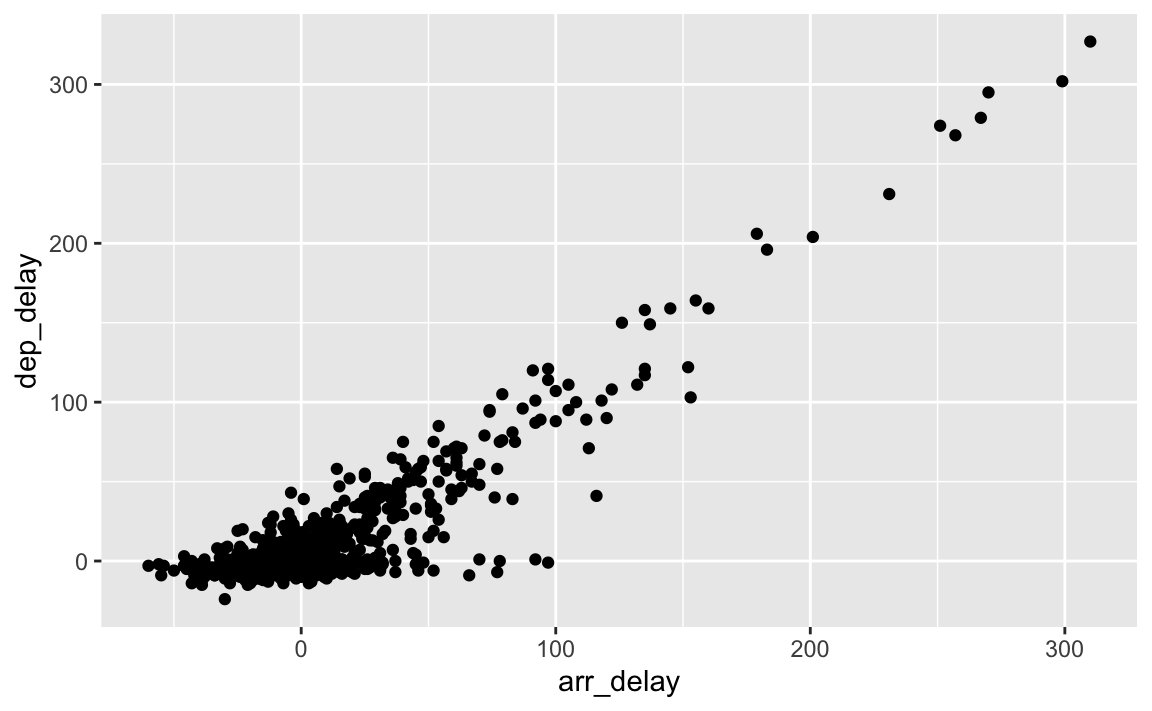
Oder vielleicht so:
flights %>%
drop_na(dep_delay, arr_delay) %>%
summarise(sd(dep_delay),
sd(arr_delay))| sd(dep_delay) | sd(arr_delay) |
|---|---|
| 40.06569 | 44.63329 |
Das sind ca. 10% Differenz in der Skalierung; wir können die Skalierung komplett angleichen, um Abweichungen, die auf unterschiedlichen Mustern beruhen, besser zu sehen. Dazu hilft uns die z-Transformation.
flights %>%
select(contains("delay")) %>%
drop_na() %>%
mutate(dep_delay = scale(dep_delay), # z-Transformation
arr_delay = scale(arr_delay)) %>% # z-Transformation
ggplot() +
aes(x = arr_delay, y = dep_delay) +
geom_bin2d() +
geom_abline(linetype = "dashed",
color = "grey60")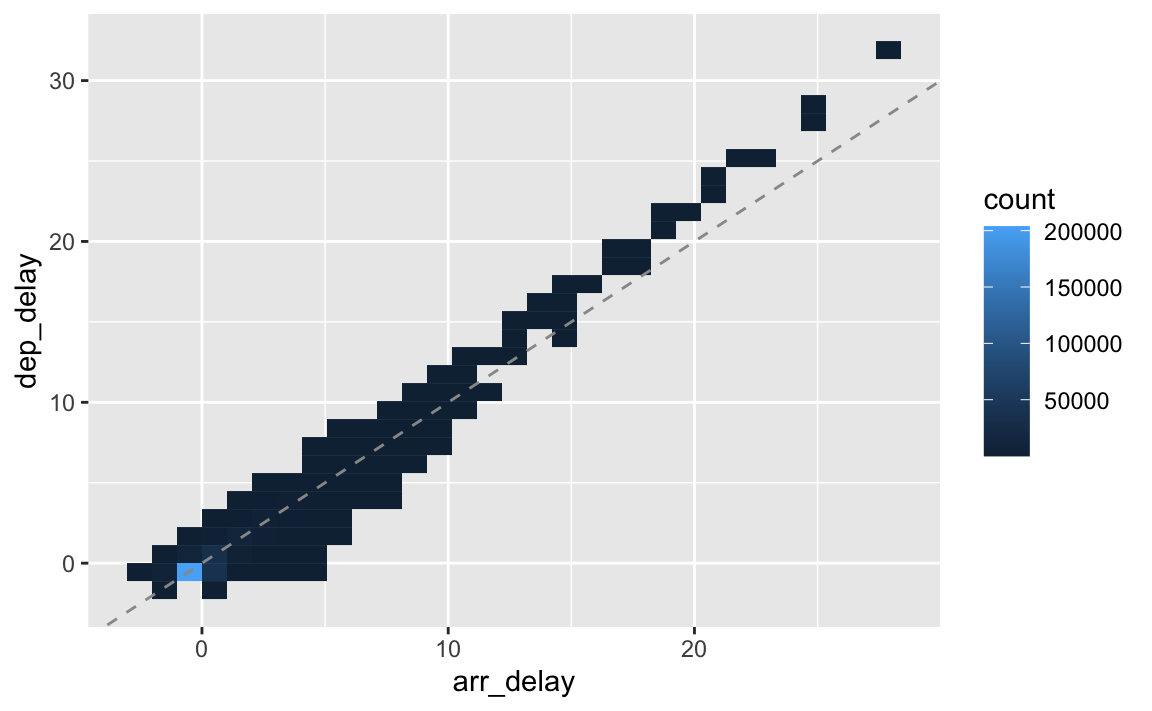
Die beiden Variablen scheinen ziemlich stark korreliert zu sein.
flights %>%
drop_na(dep_delay, arr_delay) %>%
summarise(cor(dep_delay, arr_delay))| cor(dep_delay, arr_delay) |
|---|
| 0.9148028 |
Ja, sind sie. Dann ist es vielleicht egal, welche der beiden Variablen wir verwenden. Nehmen wir dep_delay.
5 Verteilung der Verspätung
flights %>%
ggplot() +
aes(x = dep_delay) %>%
geom_density()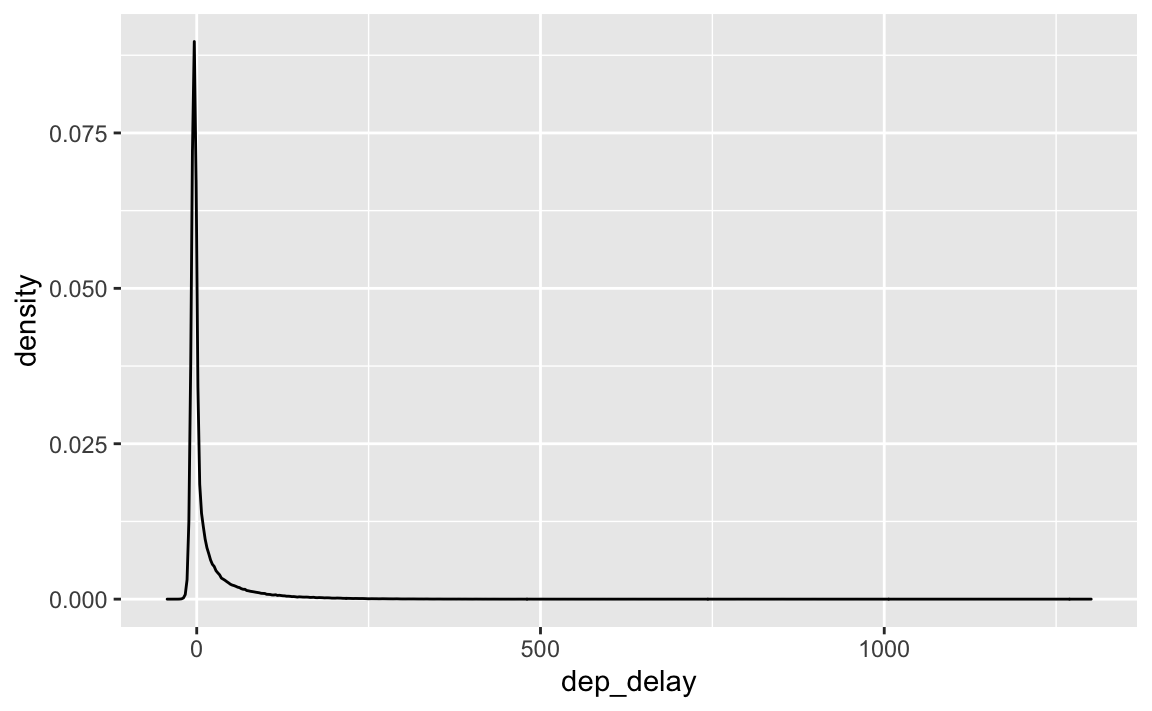
Ein sehr langer rechter Rand; die meisten Flüge sind nicht/kaum verspätet; aber einige wenige sind sehr stark verspätet.
Zentrale deskriptive Statisitken könnte man sich mit summary ausgeben lassen:
flights %>%
filter(!is.na(dep_delay)) %>% # keine fehlenden Werte
summarise(depdelay_mean = mean(dep_delay),
depdelay_sd = sd(dep_delay),
depdelay_md = median(dep_delay),
depdelay_iqr = IQR(dep_delay)) | depdelay_mean | depdelay_sd | depdelay_md | depdelay_iqr |
|---|---|---|---|
| 12.63907 | 40.21006 | -2 | 16 |
Oder man benutzt den Befehl across, der es erlaubt, eine oder mehrere Funktionen auf eine oder mehrere Spalten anzuwenden. In diesem Beispiel wenden wir mehrere Funktionen (adressiert mit .fns) auf eine Spalte (dep_delay), adressiert mit dem Argument .cols an. Außerdem kann man die Namen der resultierenden Spalten bestimmen mit dem Argument .names. In der geschweiften Klammer steht eine interne Variable, die den Namen der jeweils berechneten Funktion ({fn}) an den Namen der neu erstellten Spalte anfügt; in der Ausgabe sieht man das gut.
flights %>%
summarise(across(
.cols = dep_delay,
.fns = list(mean = mean,
md = median,
sd = sd,
iqr = IQR), na.rm = TRUE,
.names = "depdelay_{fn}"
))| depdelay_mean | depdelay_md | depdelay_sd | depdelay_iqr |
|---|---|---|---|
| 12.63907 | -2 | 40.21006 | 16 |
5.1 flights2: Extremwerte (der Verspätung) definieren
Es gibt keinen sicheren Weg, mit Extremwerten umzugehen. Häufig macht es Sinn, die Ergebnisse zu vergleichen mit oder ohne Extremwerten.
"Wann ist ein Flug sehr verspätet?
5.1.1 Boxplot-Methode
Eine Möglichkeit ist die “Boxplot-Methode”: Entferne alle Flüge, die mehr verspätet sind als: \(q75+1.5iqr\)
Definieren wir als Extremwert, wenn eine Verspätung zu den 25% Flügen mit der größten Verspätung gehört.
flights %>%
summarise(q75 = quantile(dep_delay,
prob = .75,
na.rm = TRUE))| q75 |
|---|
| 11 |
Das sind also etwa 11 Minuten, die die Grenzlinie zwischen den 75% weniger bzw. den 25% stärker verspäteten Flügen markieren.
Dann berechnen wir den IQR:
flights %>%
summarise(depdelay_iqr = IQR(dep_delay, na.rm = TRUE))| depdelay_iqr |
|---|
| 16 |
Der Grenzwert liegt dem zufolge bei:
grenzwert <- 11 + 1.5*16Das ist kein “gottgegebener” Wert, sondern ein pragmatischer Versuch, einen Grenzwert zu finden. Die Nützlichkeit dieses Grenzwerts müsste sich noch erweisen. Viele andere Grenzwerte lassen sich verteidigen.
flights2 <-
flights %>%
mutate(is_extreme = case_when(
dep_delay > 11 + 1.5 * 16 ~ TRUE, # Verspätung > 35 Min.
dep_delay <= 35 ~ FALSE # in den anderen Fällen (<= 35 Min.), dann kein Extremwert
))5.2 Fehlende Werte berechnen
Wie viele fehlende Werte gibt es eigentlich?
flights %>%
summarise(sum(is.na(dep_delay))) # fehlende Werte zählen| sum(is.na(dep_delay)) |
|---|
| 8255 |
So geht es für alle Spalten auf einmal:
flights %>%
summarise(across(everything(), ~ sum(is.na(.x))))| X1 | year | month | day | dep_time | sched_dep_time | dep_delay | arr_time | sched_arr_time | arr_delay | carrier | flight | tailnum | origin | dest | air_time | distance | hour | minute | time_hour |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 8255 | 0 | 8255 | 8713 | 0 | 9430 | 0 | 0 | 2512 | 0 | 0 | 9430 | 0 | 0 | 0 | 0 |
Übrigens hätten wir die Anzahl der fehlenden Werte auch mit skim() in Erfahrung bringen können.
Wie viele Fälle gingen verloren, wenn wir die Fälle mit fehlenden Werten bei dep_delay entfernten?
flights %>%
drop_na(dep_delay) %>%
nrow()
#> [1] 328521Und wenn wir alle fehlenden Werte entfernen würden?
flights %>%
drop_na() %>%
nrow()
#> [1] 327346Wir verlieren nicht viele Fälle mehr, wenn wir die fehlenden Werte aller Variablen (Spalten) entfernen. Also machen wir das mal.
5.3 flights3
Achtung: dieses Vorgehen hier ist gefährlich. U.U. verliert man sehr viele Zeilen (Beobachtungen).
flights3 <-
flights2 %>%
drop_na() %>%
select(-year)Die Spalte year ist kontant (immer der Wert “2013”); daher ist die Spalte nutzlos, sie birgt keine Information. Wir können sie gefahrlos löschen.
6 Deskriptive Statistiken
6.1 Mit summarise
Das kann machen mit summarise. Einfach, kann aber viel Tipperei bedeuten:
flights2 %>%
summarise(mean(dep_delay),
sd(dep_delay),
mean(arr_delay),
sd(arr_delay)) # und so weiter| mean(dep_delay) | sd(dep_delay) | mean(arr_delay) | sd(arr_delay) |
|---|---|---|---|
| NA | NA | NA | NA |
6.2 Mit skimr
skimr ist sehr praktisch; man bekommt viele Statistiken auf einmal gezeigt; das spart viel Tipperei.
flights %>%
skim()| Name | Piped data |
| Number of rows | 336776 |
| Number of columns | 20 |
| _______________________ | |
| Column type frequency: | |
| character | 4 |
| numeric | 15 |
| POSIXct | 1 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| carrier | 0 | 1.00 | 2 | 2 | 0 | 16 | 0 |
| tailnum | 2512 | 0.99 | 5 | 6 | 0 | 4043 | 0 |
| origin | 0 | 1.00 | 3 | 3 | 0 | 3 | 0 |
| dest | 0 | 1.00 | 3 | 3 | 0 | 105 | 0 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| X1 | 0 | 1.00 | 168388.50 | 97219.00 | 1 | 84194.75 | 168388.5 | 252582.2 | 336776 | ▇▇▇▇▇ |
| year | 0 | 1.00 | 2013.00 | 0.00 | 2013 | 2013.00 | 2013.0 | 2013.0 | 2013 | ▁▁▇▁▁ |
| month | 0 | 1.00 | 6.55 | 3.41 | 1 | 4.00 | 7.0 | 10.0 | 12 | ▇▆▆▆▇ |
| day | 0 | 1.00 | 15.71 | 8.77 | 1 | 8.00 | 16.0 | 23.0 | 31 | ▇▇▇▇▆ |
| dep_time | 8255 | 0.98 | 1349.11 | 488.28 | 1 | 907.00 | 1401.0 | 1744.0 | 2400 | ▁▇▆▇▃ |
| sched_dep_time | 0 | 1.00 | 1344.25 | 467.34 | 106 | 906.00 | 1359.0 | 1729.0 | 2359 | ▁▇▇▇▃ |
| dep_delay | 8255 | 0.98 | 12.64 | 40.21 | -43 | -5.00 | -2.0 | 11.0 | 1301 | ▇▁▁▁▁ |
| arr_time | 8713 | 0.97 | 1502.05 | 533.26 | 1 | 1104.00 | 1535.0 | 1940.0 | 2400 | ▁▃▇▇▇ |
| sched_arr_time | 0 | 1.00 | 1536.38 | 497.46 | 1 | 1124.00 | 1556.0 | 1945.0 | 2359 | ▁▃▇▇▇ |
| arr_delay | 9430 | 0.97 | 6.90 | 44.63 | -86 | -17.00 | -5.0 | 14.0 | 1272 | ▇▁▁▁▁ |
| flight | 0 | 1.00 | 1971.92 | 1632.47 | 1 | 553.00 | 1496.0 | 3465.0 | 8500 | ▇▃▃▁▁ |
| air_time | 9430 | 0.97 | 150.69 | 93.69 | 20 | 82.00 | 129.0 | 192.0 | 695 | ▇▂▂▁▁ |
| distance | 0 | 1.00 | 1039.91 | 733.23 | 17 | 502.00 | 872.0 | 1389.0 | 4983 | ▇▃▂▁▁ |
| hour | 0 | 1.00 | 13.18 | 4.66 | 1 | 9.00 | 13.0 | 17.0 | 23 | ▁▇▇▇▅ |
| minute | 0 | 1.00 | 26.23 | 19.30 | 0 | 8.00 | 29.0 | 44.0 | 59 | ▇▃▆▃▅ |
Variable type: POSIXct
| skim_variable | n_missing | complete_rate | min | max | median | n_unique |
|---|---|---|---|---|---|---|
| time_hour | 0 | 1 | 2013-01-01 05:00:00 | 2013-12-31 23:00:00 | 2013-07-03 10:00:00 | 6936 |
7 Korrelate von Verspätung
Schauen wir, welche Variablen mit dep_delay, der Verspätung der Flüge also, korrelieren.
7.1 Metrische Prädiktoren
7.1.1 Nur mit cor
Am einfachsten geht es so. Der Nachteil ist mehr (viel) Tipperei:
flights3 %>%
select(where(is.numeric)) %>%
summarise(cor_month = cor(dep_delay, month),
cor_day = cor(dep_delay, day),
cor_dep_time = cor(dep_delay, dep_time)) # etc| cor_month | cor_day | cor_dep_time |
|---|---|---|
| -0.0200547 | 0.0005914 | 0.2596127 |
7.1.2 Mit across
Berechnen wir die Korrelationen jetzt mit dem Befehl across. Der Punkt . spricht hier jeweils eine Spalte an, die von across ausgewählt wurde. Der Effekt ist, dass eine Korrelation von jeder Spalte mit dep_delay berechnet wird.
flights3 %>%
select(where(is.numeric)) %>% # nur die numerischen Spalten auswählen
summarise(across(
.cols = everything(),
.fns = ~ cor(., dep_delay))) %>%
pivot_longer(everything()) %>% # von breit auf lang
arrange(-value) # absteigend sortieren| name | value |
|---|---|
| dep_delay | 1.0000000 |
| arr_delay | 0.9148028 |
| dep_time | 0.2596127 |
| sched_dep_time | 0.1989235 |
| hour | 0.1982692 |
| sched_arr_time | 0.1604972 |
| flight | 0.0539697 |
| X1 | 0.0491868 |
| arr_time | 0.0294210 |
| minute | 0.0282514 |
| day | 0.0005914 |
| month | -0.0200547 |
| distance | -0.0216809 |
| air_time | -0.0224051 |
7.1.3 Mit correlate
Oder so, das ist vielleicht einfacher:
flights2 %>%
select(where(is.numeric)) %>% # alle metrischen Variablen, aber sonst keine
correlate() %>% # korreliere, was du hast
focus(dep_delay) %>% # beschränke (fokussiere) dich auf `dep_delay`
arrange(-dep_delay)| term | dep_delay |
|---|---|
| arr_delay | 0.9148028 |
| dep_time | 0.2602312 |
| sched_dep_time | 0.1988867 |
| hour | 0.1982259 |
| sched_arr_time | 0.1604885 |
| flight | 0.0547337 |
| X1 | 0.0497132 |
| arr_time | 0.0287288 |
| minute | 0.0284409 |
| day | 0.0004200 |
| month | -0.0200570 |
| distance | -0.0216708 |
| air_time | -0.0224051 |
| year | NA |
7.2 Nominale Prädiktoren
flights2 %>%
select(where(negate(is.numeric))) %>%
names()
#> [1] "carrier" "tailnum" "origin" "dest" "time_hour"
#> [6] "is_extreme"flights2 %>%
select(where(negate(is.numeric))) %>%
summarise(across(
.cols = everything(),
.fns = list(ndist = n_distinct)
)) %>%
pivot_longer(everything())| name | value |
|---|---|
| carrier_ndist | 16 |
| tailnum_ndist | 4044 |
| origin_ndist | 3 |
| dest_ndist | 105 |
| time_hour_ndist | 6936 |
| is_extreme_ndist | 3 |
Geht auch mit skim, s. oben, ist einfacher.
7.2.1 Carrier
carrier ist die Fluggesellschaft.
Wie viele verschiedene Fluggesellschaften gibt es?
Wie viele Flüge hat jede davon ausgeführt?
Welche Fluggesellschaft hat die meisten Flüge ausgeführt?
Gibt es große Unterschiede in de Zahl der ausgeführten Flüge.
Wer hat eigentlich die flüssige Seife erfunden?
Fragen über Fragen.
flights2 %>%
select(carrier) %>%
count(carrier, sort = TRUE) | carrier | n |
|---|---|
| UA | 58665 |
| B6 | 54635 |
| EV | 54173 |
| DL | 48110 |
| AA | 32729 |
| MQ | 26397 |
| US | 20536 |
| 9E | 18460 |
| WN | 12275 |
| VX | 5162 |
| FL | 3260 |
| AS | 714 |
| F9 | 685 |
| YV | 601 |
| HA | 342 |
| OO | 32 |
Wir brauchen eine Visualisierung dazu; das beantwortet vielleicht einen Teil der obigen Fragen.
plot1 <- flights2 %>%
select(carrier) %>%
count(carrier, sort = TRUE) %>%
ggplot() +
aes(y = carrier, x = n) +
geom_point(color = "red") +
geom_line(group = 1)
plot1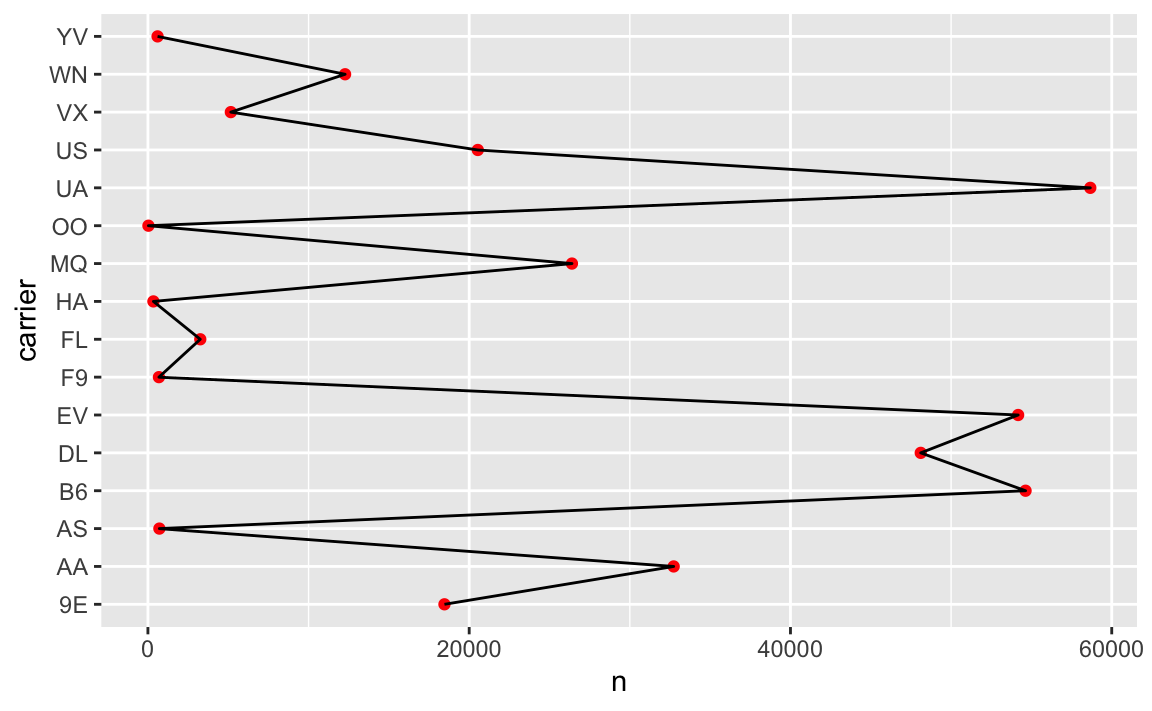
Wir müssen die Werte von carrier sortieren anhand der Anzahl der Flüge, sonst ist es zu unübersichtlich.
7.2.2 Achsen-Labels anpassen
Dieser Abschnitt ist zur Vertiefung, er ist nicht inhaltlich wichtig
Sagen wir, wir möchten die Labels der X-Achse anpassen, und zwar möchten wir die Werte 25.000, 50.000, und 75.0000.
plot1 +
scale_x_continuous(breaks = c(0, 25000, 50000, 75000),
limits = c(0, 100000),
labels = c("keine", "wenig", "mittel", "viel"))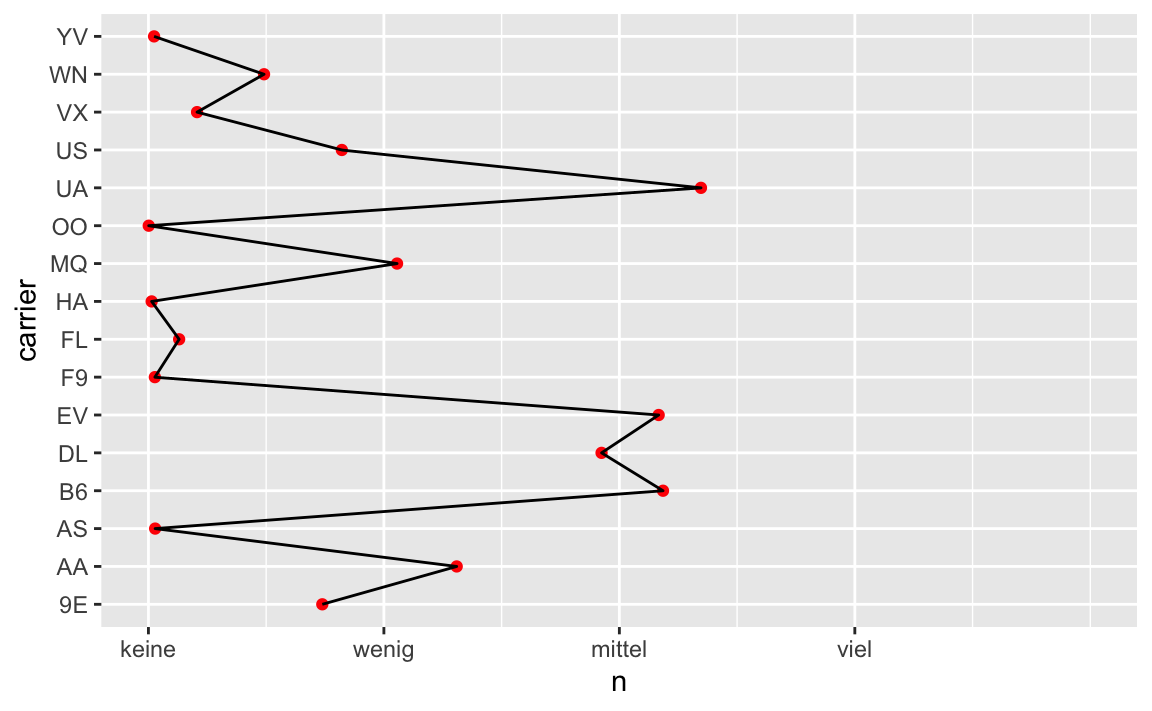
Hm, schön sieht es noch nicht aus; die limits machen nicht unbedingt Sinn. Die labels sind auch wenig sinnvoll.
Mehr zum Thema “Achsen aufhübschen” findet sich z.B. hier.
7.2.3 “Lumpsensammler-Kategorie”
flights2 <-
flights2 %>%
mutate(carrier = factor(carrier)) %>% # nicht character, sondern factor
mutate(carrier_lump = fct_lump(carrier, n = 8))Hier fassen wir mit fct_lump alle Stufen von carrier zu acht Stufen (daher n = 8) zusammen plus einer “Lumpensammler-Kategorie” zusammen.
Dazu muss die Variable aber als factor vorliegen, was wir in der Zeile davor erledigt haben.
Jetzt haben wir noch nur 9 (8 plus Lumpensammler-Gruppe) Gruppen:
flights2 %>%
count(carrier_lump)| carrier_lump | n |
|---|---|
| 9E | 18460 |
| AA | 32729 |
| B6 | 54635 |
| DL | 48110 |
| EV | 54173 |
| MQ | 26397 |
| UA | 58665 |
| US | 20536 |
| Other | 23071 |
Liniendiagramm:
flights2 %>%
select(carrier) %>%
count(carrier, sort = TRUE) %>%
ggplot() +
aes(y = fct_reorder(carrier, n), x = n) +
geom_point(color = "red") +
geom_line(group = 1)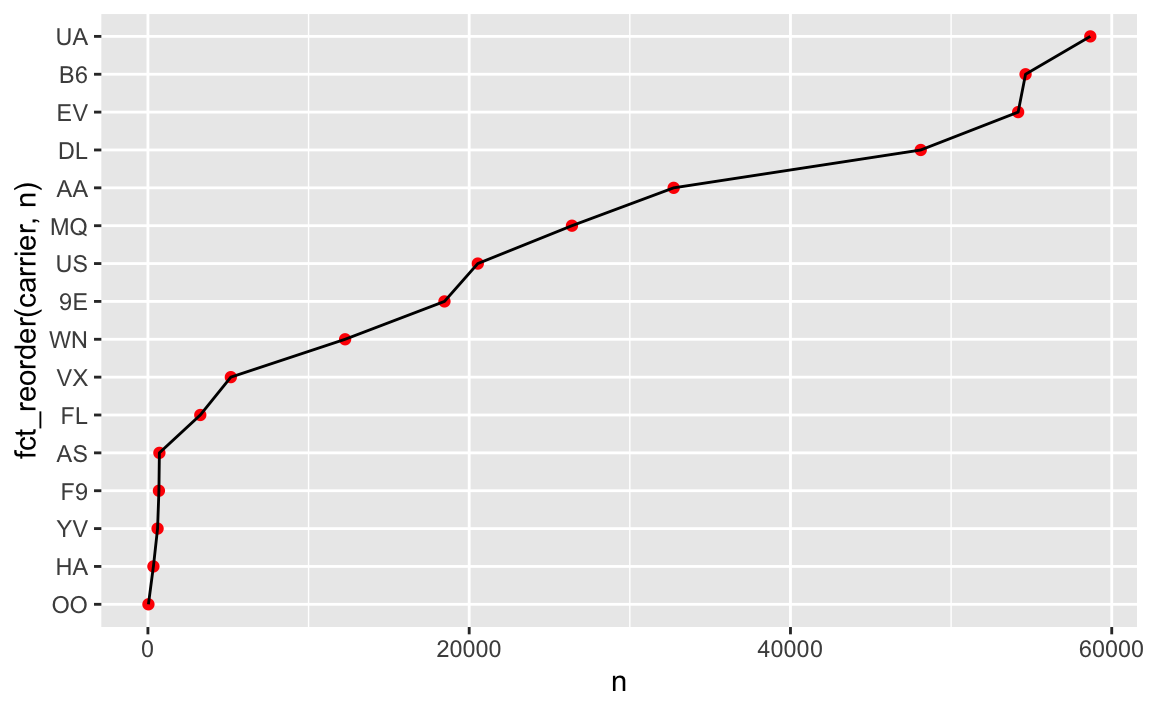
Mit fct_reorder haben wir die Werte von carrier (UA, B6, AA, …) sortiert und zwar anhand der Werte von n, also anhand der Häufigkeit. Es resultiert eine Rangfolge: UA > B6 > EV > DL > ... etc.
(Nur) Mit einer sortierten Faktorvariable lässt sich so eine Art von Diagramm gut sortiert darstellen.
Ah, schon besser. Aber recht informationsarm, das Diagramm. Informationsreicher ist ein Boxplot:
flights2 %>%
filter(!is_extreme) %>% # keine Extremwerte
ggplot() +
aes(x = fct_reorder(carrier_lump, dep_delay,
na.rm = TRUE),
y = dep_delay) %>%
geom_boxplot()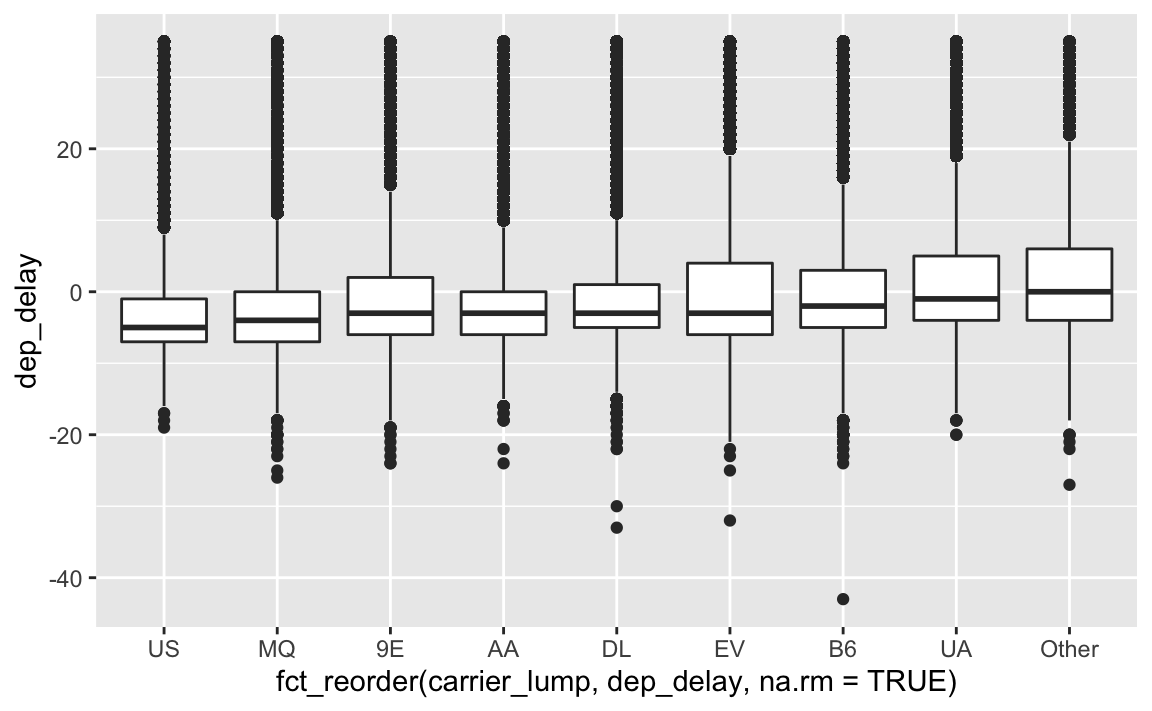
Eine alternative Darstellung wäre ein Letter Value Plot.
Schauen wir uns mal die Mediane genauer an:
flights2 %>%
filter(!is_extreme) %>%
group_by(carrier_lump) %>%
summarise(dep_delay = median(dep_delay, na.rm = TRUE)) %>%
arrange(dep_delay)| carrier_lump | dep_delay |
|---|---|
| US | -5 |
| MQ | -4 |
| 9E | -3 |
| AA | -3 |
| DL | -3 |
| EV | -3 |
| B6 | -2 |
| UA | -1 |
| Other | 0 |
Die Reihenfolge entspricht der dem obigen Diagramm.
7.3 Korrelation von carrier mit Verspätung
Hier mit “Dummysierung” aller nicht-numerischer Spalten. Ein Beispiel zur Verdeutlichung:
flights2 <-
flights2 %>%
mutate(
originJFK = case_when(
origin == "JFK" ~ 1,
origin != "JFK" ~ 0
),
originLGA = case_when(
origin == "LGA" ~ 1,
TRUE ~ 0,
)
)flights2 %>%
select(origin, originJFK, originLGA) %>%
slice(1:5)| origin | originJFK | originLGA |
|---|---|---|
| EWR | 0 | 0 |
| LGA | 0 | 1 |
| JFK | 1 | 0 |
| JFK | 1 | 0 |
| LGA | 0 | 1 |
Diese Art der Umwandlung von mehrstufig-nominal in eine binäre Varialbe (0-1-Variable, oder “Indikatorvariable”) kann auch z.B. mit der Funktion dummy_cols() (auf “fastDummies”) bewerkstelligen lassen:
flights2 %>%
select(origin, dep_delay) %>%
dummy_cols() %>% # aus dem Paket `fastDummies`
head() # slice(1:6)| origin | dep_delay | origin_EWR | origin_JFK | origin_LGA |
|---|---|---|---|---|
| EWR | 2 | 1 | 0 | 0 |
| LGA | 4 | 0 | 0 | 1 |
| JFK | 2 | 0 | 1 | 0 |
| JFK | -1 | 0 | 1 | 0 |
| LGA | -6 | 0 | 0 | 1 |
| EWR | -4 | 1 | 0 | 0 |
Mit den “dummyisierten” Spalten können wir jetzt Korrelationen rechnen, denn jetzt haben wir Zahlen. Achtung: Die Variablen bleiben nominalskaliert, trotz der 0-1-Transformation. Auf diese Art Korrelationen zu berechnen ist nur für dummysierte Variablen (“Indikatorvariablen”) sinnvoll. Die Schiefe der Verteilung begrenzt hier übrigens die Stärke der Korrelation.
flights2 %>%
select(dep_delay, carrier) %>%
dummy_cols() %>% # "Dummysierung"
select(-carrier) %>%
pivot_longer(-dep_delay,
names_to = "carrier",
values_to = "value") %>%
group_by(carrier) %>%
summarise(cor_depdelay_carrier = cor(dep_delay, value,
use = "complete.obs")) %>%
arrange(-abs(cor_depdelay_carrier)) %>%
filter(abs(cor_depdelay_carrier) > 0.10)| carrier | cor_depdelay_carrier |
|---|
Keine Korrelation war (im Betrag) größer als 0.1.
Zur Erinnerung: Es ist nicht unbedingt nötig, die “Dummyisierung” durchzuführen, ein einfaches Vergleichen der Mittelwerte (oder Mediane) mit ihrer Streuung führt zu einem ähnlichen Ergebnis.
Die Regression mit lm führt für Sie automatisch die Dummyisierung durch.
7.3.1 Hour
flights2 %>%
filter(!is_extreme) %>%
select(dep_delay, hour) %>%
mutate(hour = factor(hour)) %>%
ggplot() +
aes(x = fct_reorder(hour, dep_delay,
na.rm = TRUE),
y = dep_delay) +
geom_boxplot()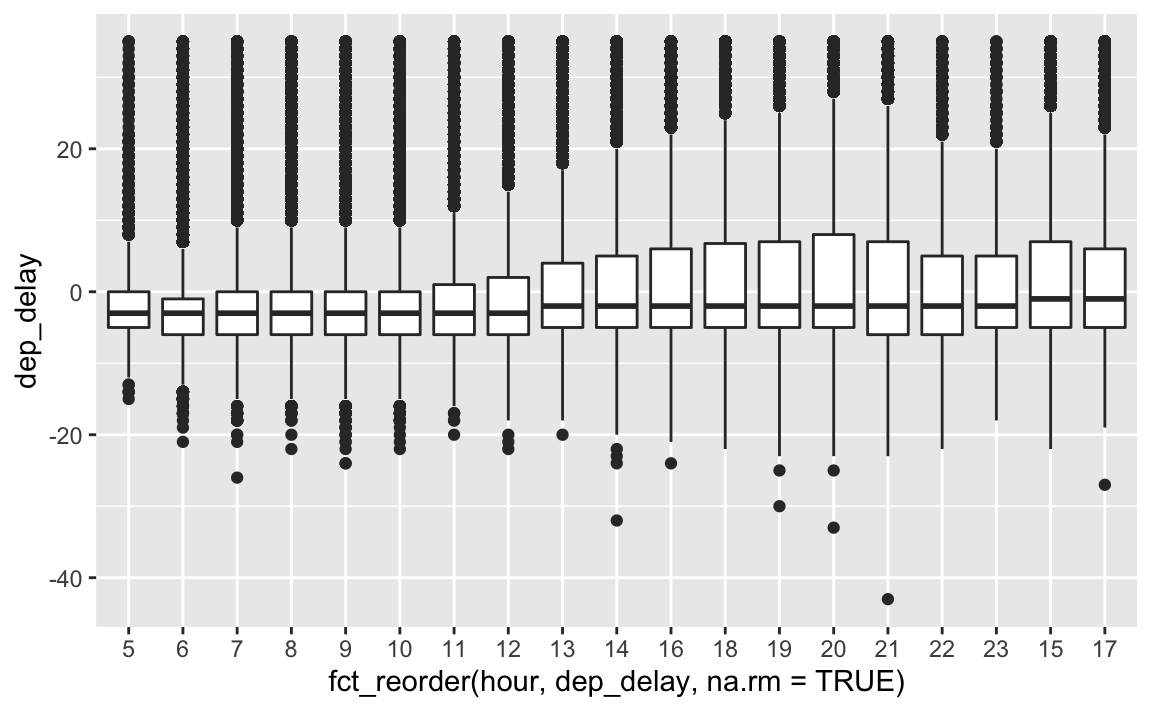
7.3.2 Origin
flights2 %>%
filter(!is_extreme) %>%
select(origin, dep_delay) %>%
ggplot() +
aes(x = origin, y = dep_delay) %>%
geom_boxplot()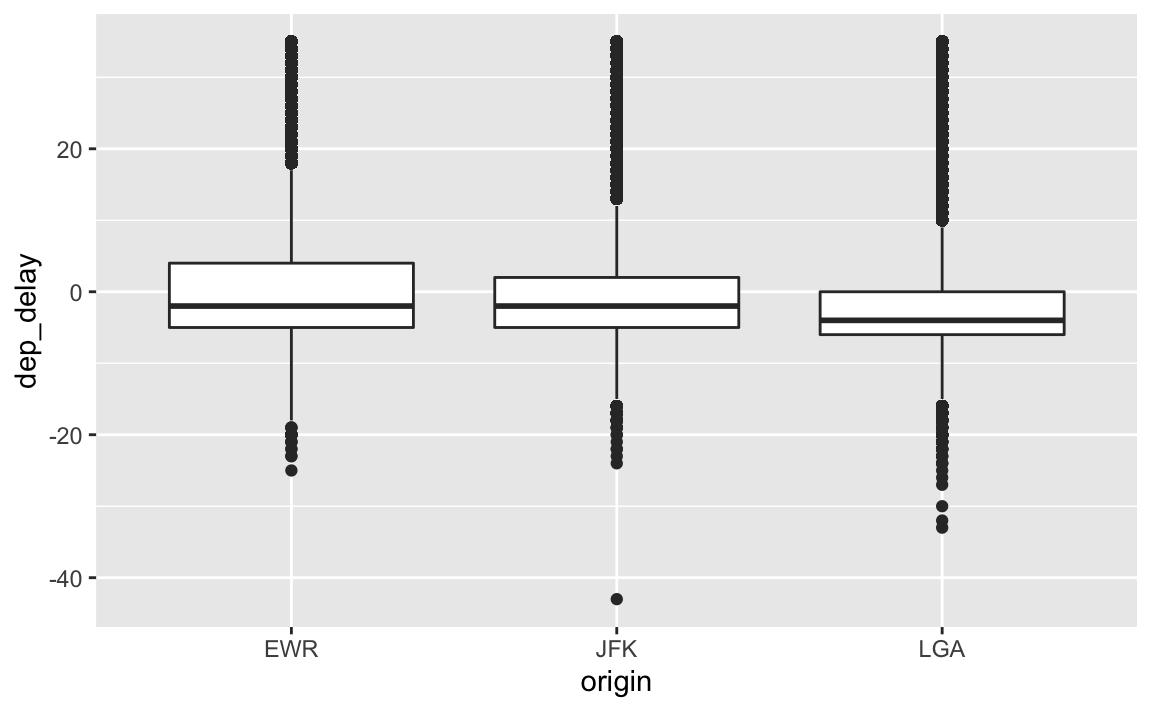
7.4 Drei Variablen: Origin, hour, dep_delay
flights2 %>%
filter(!is_extreme) %>%
select(origin, dep_delay, hour) %>%
mutate(hour = factor(hour, levels = 5:23)) %>%
ggplot() +
aes(x = hour, y = dep_delay) +
geom_boxplot() +
facet_wrap(~ origin)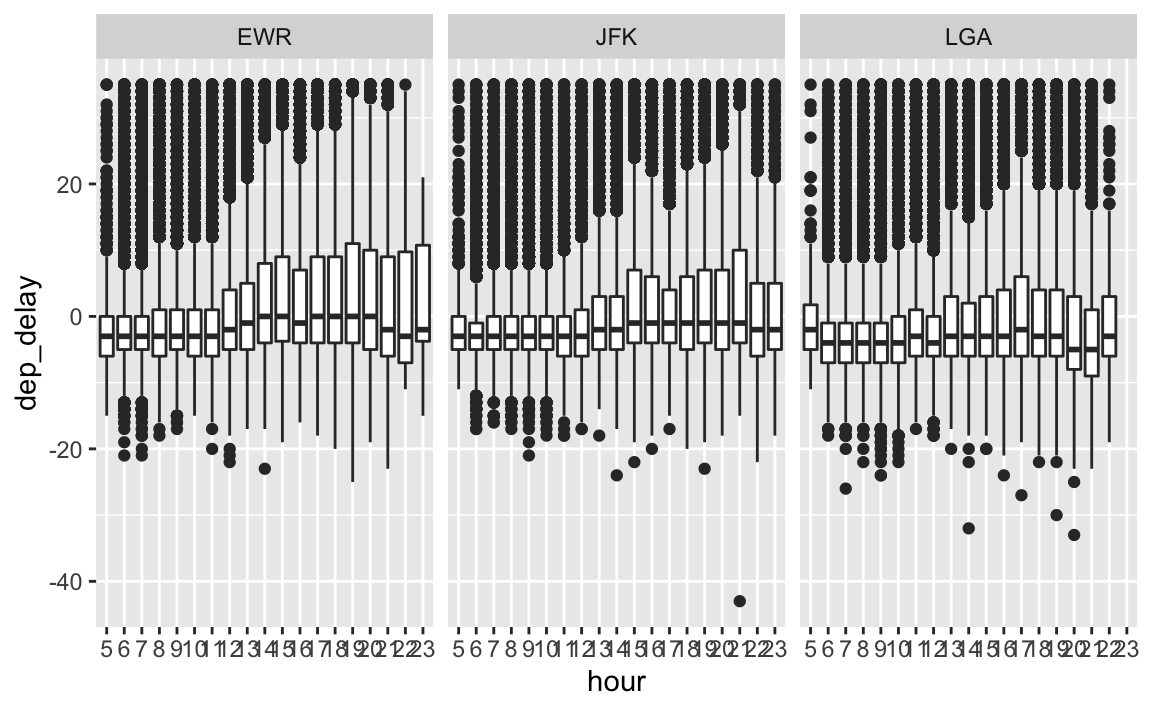
7.5 Alle nominale Variablen
Natürlich könnte man “händisch” alle nominalskalierten Variablen explizit benennen, etwa so:
flights3 %>%
select(carrier, tailnum, origin, dest, time_hour) %>%
slice(1:3)| carrier | tailnum | origin | dest | time_hour |
|---|---|---|---|---|
| UA | N14228 | EWR | IAH | 2013-01-01 05:00:00 |
| UA | N24211 | LGA | IAH | 2013-01-01 05:00:00 |
| AA | N619AA | JFK | MIA | 2013-01-01 05:00:00 |
Aber es geht auch etwas “cooler” mit weniger Tipperei:
flights3 %>%
select(where(~ !is.numeric(.))) %>%
names()
#> [1] "carrier" "tailnum" "origin" "dest" "time_hour"
#> [6] "is_extreme"7.6 flights4
flights4 <-
flights3 %>%
mutate(dest = fct_lump_prop(dest, prop = .025)) Mit fct_lump_prop fassen wir alle Stufen zu einer zusammen, die jeweils weniger als 2.5% ausmachen.
flights4 %>%
count(dest, sort = T)| dest | n |
|---|---|
| Other | 172061 |
| ATL | 16837 |
| ORD | 16566 |
| LAX | 16026 |
| BOS | 15022 |
| MCO | 13967 |
| CLT | 13674 |
| SFO | 13173 |
| FLL | 11897 |
| MIA | 11593 |
| DCA | 9111 |
| DTW | 9031 |
| DFW | 8388 |
flights4 %>%
filter(!is_extreme) %>%
select(dep_delay, dest, origin, carrier) %>%
group_by(dest, origin, carrier) %>%
summarise(depdelay_md = median(dep_delay, na.rm = T)) %>%
ggplot() +
aes(x = origin, y = depdelay_md, color = origin) +
facet_grid(dest ~ carrier) +
geom_point()
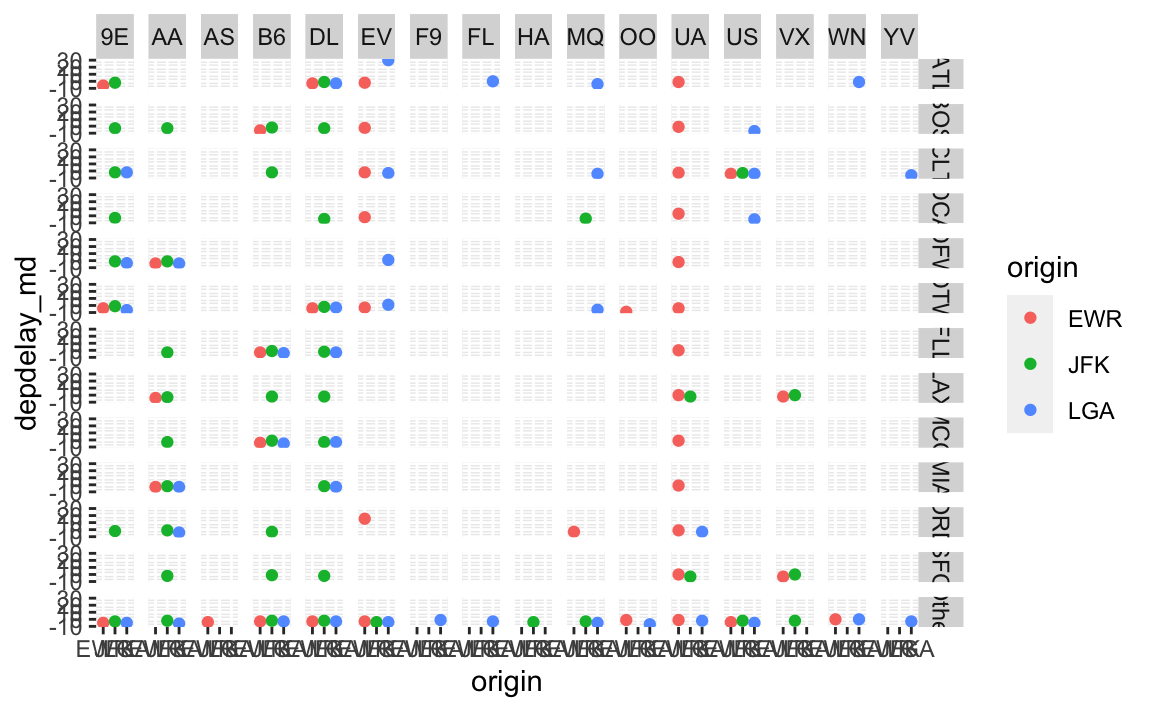
Puh, das Diagramm ist nicht sehr aussagekräftig. Vielleicht besser als Tabelle?
flights4 %>%
filter(!is_extreme) %>%
select(dep_delay, dest, origin, carrier) %>%
group_by(dest, origin, carrier) %>%
summarise(depdelay_md = median(dep_delay, na.rm = T))
#> # A tibble: 128 x 4
#> # Groups: dest, origin [37]
#> dest origin carrier depdelay_md
#> <fct> <chr> <chr> <dbl>
#> 1 ATL EWR 9E -6
#> 2 ATL EWR DL -3
#> 3 ATL EWR EV -2
#> 4 ATL EWR UA -1
#> 5 ATL JFK 9E -2
#> 6 ATL JFK DL -1
#> 7 ATL LGA DL -3
#> 8 ATL LGA EV 30
#> 9 ATL LGA FL 0
#> 10 ATL LGA MQ -4
#> # … with 118 more rowsHm, ist auch nicht gerade nützlich.
Das Beispiel zeigt, dass die Datenvisualisierung bei einer größeren Zahl an Dimensionen und/oder vielen Werten an ihre Grenzen kommen kann.
7.7 Anzahl von Flüge
flights4_sum <-
flights4 %>%
filter(!is_extreme) %>%
select(month, origin, dep_delay) %>%
drop_na() %>%
group_by(month, origin) %>%
summarise(delay_md = median(dep_delay),
delay_iqr = IQR(dep_delay),
delay_n = n()) %>%
mutate(month = factor(month),
delay_n = as.numeric(delay_n))
flights4 %>%
filter(!is_extreme) %>%
select(month, origin, dep_delay) %>%
mutate(month = factor(month)) %>%
drop_na() %>%
ggplot() +
aes(x = month, y = dep_delay, color = origin) +
geom_violin() +
geom_point(data = flights4_sum,
aes(y = delay_md,
x = month)) +
facet_wrap( ~ origin)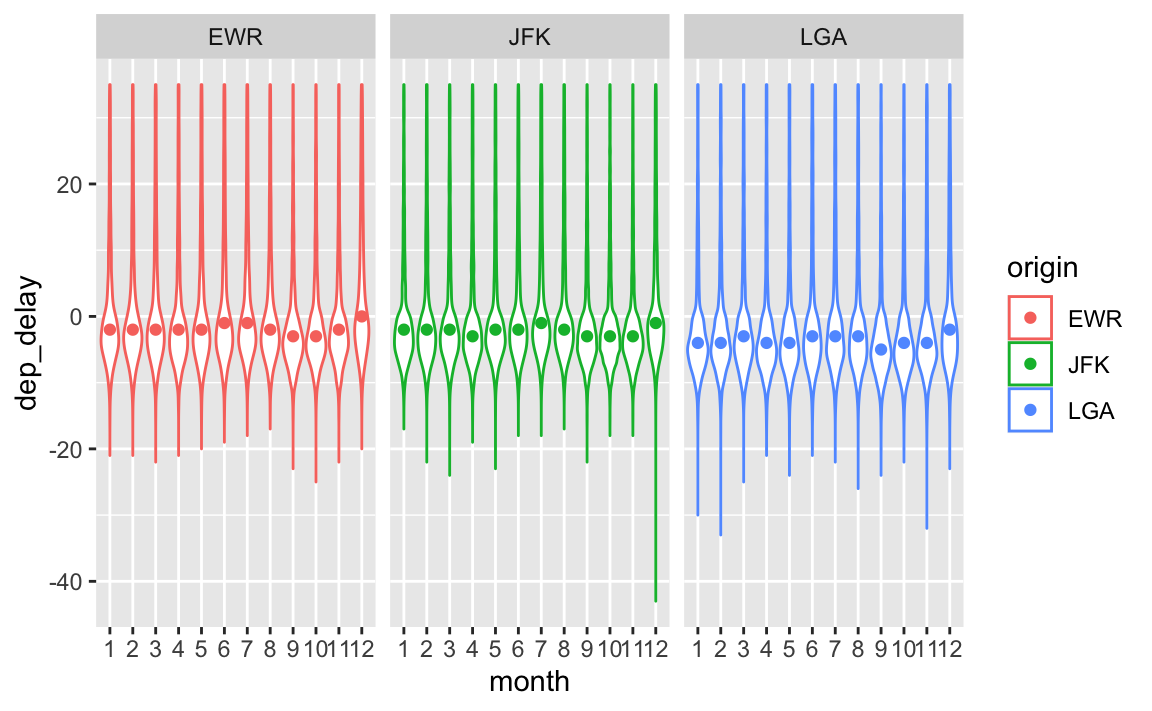
8 Fazit
Keine heiße Spur bisher. Allerdings erlaubt explorative Datenanalyse nur die gleichzeitige Betrachtung von zwei bis drei, vielleicht vier Variablen. Sind die Zusammenhänge komplizierter in dem Sinne, dass mehrere Variablen für einen Effekt zusammenwirken, so ist es mit explorativen Methoden schwer zu finden.
Der nächste logische Schritt: Wir müssen modellieren. Mit Modellierungsmethoden lassen sich auch hochdimensionale Zusammenhänge finden.
9 Achtung
Diese Analyse ist rein explorativ in dem Sinne, dass keine Hypothesen getestet werden. Es ist damit zu rechnen, dass falsch-positive Befunde auftauchen. Alle Ergebnisse sollten anhand neuer Daten validiert werden.
10 Reproduzierbarkeit
#> ─ Session info ───────────────────────────────────────────────────────────────────────────────────────────────────────
#> setting value
#> version R version 4.1.0 (2021-05-18)
#> os macOS Big Sur 10.16
#> system x86_64, darwin17.0
#> ui X11
#> language (EN)
#> collate en_US.UTF-8
#> ctype en_US.UTF-8
#> tz Europe/Berlin
#> date 2021-06-22
#>
#> ─ Packages ───────────────────────────────────────────────────────────────────────────────────────────────────────────
#> package * version date lib source
#> assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.1.0)
#> backports 1.2.1 2020-12-09 [1] CRAN (R 4.1.0)
#> blogdown 1.3 2021-04-14 [2] CRAN (R 4.1.0)
#> bookdown 0.22 2021-04-22 [2] CRAN (R 4.1.0)
#> broom 0.7.6 2021-04-05 [1] CRAN (R 4.1.0)
#> bslib 0.2.5.1 2021-05-18 [1] CRAN (R 4.1.0)
#> cachem 1.0.5 2021-05-15 [2] CRAN (R 4.1.0)
#> callr 3.7.0 2021-04-20 [1] CRAN (R 4.1.0)
#> cellranger 1.1.0 2016-07-27 [1] CRAN (R 4.1.0)
#> cli 2.5.0 2021-04-26 [1] CRAN (R 4.1.0)
#> codetools 0.2-18 2020-11-04 [2] CRAN (R 4.1.0)
#> colorspace 2.0-1 2021-05-04 [1] CRAN (R 4.1.0)
#> crayon 1.4.1 2021-02-08 [1] CRAN (R 4.1.0)
#> data.table 1.14.0 2021-02-21 [1] CRAN (R 4.1.0)
#> DBI 1.1.1 2021-01-15 [1] CRAN (R 4.1.0)
#> dbplyr 2.1.1 2021-04-06 [1] CRAN (R 4.1.0)
#> desc 1.3.0 2021-03-05 [2] CRAN (R 4.1.0)
#> devtools 2.4.1 2021-05-05 [2] CRAN (R 4.1.0)
#> digest 0.6.27 2020-10-24 [1] CRAN (R 4.1.0)
#> dplyr * 1.0.6 2021-05-05 [1] CRAN (R 4.1.0)
#> ellipsis 0.3.2 2021-04-29 [1] CRAN (R 4.1.0)
#> evaluate 0.14 2019-05-28 [1] CRAN (R 4.1.0)
#> fansi 0.5.0 2021-05-25 [1] CRAN (R 4.1.0)
#> farver 2.1.0 2021-02-28 [1] CRAN (R 4.1.0)
#> fastDummies * 1.6.3 2020-11-29 [1] CRAN (R 4.1.0)
#> fastmap 1.1.0 2021-01-25 [2] CRAN (R 4.1.0)
#> forcats * 0.5.1 2021-01-27 [1] CRAN (R 4.1.0)
#> fs 1.5.0 2020-07-31 [1] CRAN (R 4.1.0)
#> generics 0.1.0 2020-10-31 [1] CRAN (R 4.1.0)
#> ggplot2 * 3.3.3 2020-12-30 [1] CRAN (R 4.1.0)
#> glue 1.4.2 2020-08-27 [1] CRAN (R 4.1.0)
#> gtable 0.3.0 2019-03-25 [1] CRAN (R 4.1.0)
#> haven 2.4.1 2021-04-23 [1] CRAN (R 4.1.0)
#> highr 0.9 2021-04-16 [1] CRAN (R 4.1.0)
#> hms 1.1.0 2021-05-17 [1] CRAN (R 4.1.0)
#> htmltools 0.5.1.1 2021-01-22 [1] CRAN (R 4.1.0)
#> httr 1.4.2 2020-07-20 [1] CRAN (R 4.1.0)
#> jquerylib 0.1.4 2021-04-26 [1] CRAN (R 4.1.0)
#> jsonlite 1.7.2 2020-12-09 [1] CRAN (R 4.1.0)
#> knitr 1.33 2021-04-24 [1] CRAN (R 4.1.0)
#> labeling 0.4.2 2020-10-20 [1] CRAN (R 4.1.0)
#> lifecycle 1.0.0 2021-02-15 [1] CRAN (R 4.1.0)
#> lubridate 1.7.10 2021-02-26 [1] CRAN (R 4.1.0)
#> magrittr 2.0.1 2020-11-17 [1] CRAN (R 4.1.0)
#> memoise 2.0.0 2021-01-26 [2] CRAN (R 4.1.0)
#> modelr 0.1.8 2020-05-19 [1] CRAN (R 4.1.0)
#> munsell 0.5.0 2018-06-12 [1] CRAN (R 4.1.0)
#> pillar 1.6.1 2021-05-16 [1] CRAN (R 4.1.0)
#> pkgbuild 1.2.0 2020-12-15 [2] CRAN (R 4.1.0)
#> pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.1.0)
#> pkgload 1.2.1 2021-04-06 [2] CRAN (R 4.1.0)
#> prettyunits 1.1.1 2020-01-24 [1] CRAN (R 4.1.0)
#> printr * 0.1.1 2021-01-27 [1] CRAN (R 4.1.0)
#> processx 3.5.2 2021-04-30 [1] CRAN (R 4.1.0)
#> ps 1.6.0 2021-02-28 [1] CRAN (R 4.1.0)
#> purrr * 0.3.4 2020-04-17 [1] CRAN (R 4.1.0)
#> R6 2.5.0 2020-10-28 [1] CRAN (R 4.1.0)
#> Rcpp 1.0.6 2021-01-15 [1] CRAN (R 4.1.0)
#> readr * 1.4.0 2020-10-05 [1] CRAN (R 4.1.0)
#> readxl 1.3.1 2019-03-13 [1] CRAN (R 4.1.0)
#> remotes 2.4.0 2021-06-02 [2] CRAN (R 4.1.0)
#> reprex 2.0.0 2021-04-02 [1] CRAN (R 4.1.0)
#> rlang 0.4.11 2021-04-30 [1] CRAN (R 4.1.0)
#> rmarkdown 2.8 2021-05-07 [1] CRAN (R 4.1.0)
#> rprojroot 2.0.2 2020-11-15 [2] CRAN (R 4.1.0)
#> rstudioapi 0.13 2020-11-12 [1] CRAN (R 4.1.0)
#> rvest 1.0.0 2021-03-09 [1] CRAN (R 4.1.0)
#> sass 0.4.0 2021-05-12 [1] CRAN (R 4.1.0)
#> scales 1.1.1 2020-05-11 [1] CRAN (R 4.1.0)
#> sessioninfo 1.1.1 2018-11-05 [2] CRAN (R 4.1.0)
#> stringi 1.6.2 2021-05-17 [1] CRAN (R 4.1.0)
#> stringr * 1.4.0 2019-02-10 [1] CRAN (R 4.1.0)
#> testthat 3.0.2 2021-02-14 [2] CRAN (R 4.1.0)
#> tibble * 3.1.2 2021-05-16 [1] CRAN (R 4.1.0)
#> tidyr * 1.1.3 2021-03-03 [1] CRAN (R 4.1.0)
#> tidyselect 1.1.1 2021-04-30 [1] CRAN (R 4.1.0)
#> tidyverse * 1.3.1 2021-04-15 [1] CRAN (R 4.1.0)
#> usethis 2.0.1 2021-02-10 [2] CRAN (R 4.1.0)
#> utf8 1.2.1 2021-03-12 [1] CRAN (R 4.1.0)
#> vctrs 0.3.8 2021-04-29 [1] CRAN (R 4.1.0)
#> withr 2.4.2 2021-04-18 [1] CRAN (R 4.1.0)
#> xfun 0.23 2021-05-15 [1] CRAN (R 4.1.0)
#> xml2 1.3.2 2020-04-23 [1] CRAN (R 4.1.0)
#> yaml 2.2.1.99 2021-06-18 [1] Github (viking/r-yaml@4788abe)
#>
#> [1] /Users/sebastiansaueruser/Library/R/x86_64/4.1/library
#> [2] /Library/Frameworks/R.framework/Versions/4.1/Resources/library