- 1 Load packages
- 2 Benötigte Pakete
- 3 Datensatz laden
- 4 Erster Blick
- 5 Metrische Variablen einzeln (univariat)
- 6 Forschungsfrage
- 7 Datensatz filtern - nur Länder, keine Landesteile
- 8 Vergleich der Lebenszufriedenheit der Länder
- 9 Zusammenhang zweier metrischer Variablen – Punktediagramm
- 10 Deskriptive Statistiken nach Ländern
- 11 Reproducibility
1 Load packages
library(tidyverse) # data wrangling
library(skimr) # Viele Statistiken auf einen BlickIn diesem Post untersuchen wir einige Aspekte der explorativen Datenanalyse für den Datensatz oecd wellbeing aus dem Jahr 2016.
Hinweis: Als Vertiefung gekennzeichnete Abschnitt sind nicht prüfungsrelevant.
2 Benötigte Pakete
Ein Standard-Paket zur grundlegenden Datenanalyse:
library(tidyverse)3 Datensatz laden
Der Datensatz kann hier bezogen werden.
Doi: https://doi.org/10.1787/data-00707-en.
Falls der Datensatz lokal (auf Ihrem Rechner) vorliegt, können Sie ihn in gewohnter Manier importieren. Geben Sie dazu den Pfad zum Datensatz ein; bei mir sieht das so aus:
oecd <- read_csv("/Users/sebastiansaueruser/datasets/oecd_wellbeing.csv")Liegt die Datendatei im gleichen Verzeichnis wie Ihre Rmd-Datei, dann brauchen Sie nur den Dateinamen, nicht den Pfad, anzugeben.
Alternativ können Sie die Daten direkt von einem Server beziehen:
oecd <- read_csv("https://raw.githubusercontent.com/sebastiansauer/2021-sose/master/data/OECD/oecd-wellbeing.csv")4 Erster Blick
glimpse(oecd)
#> Rows: 429
#> Columns: 15
#> $ Country <chr> "Australia", "Australia", "Australia", "Austr…
#> $ Region <chr> "New South Wales", "Victoria", "Queensland", …
#> $ region_type <chr> "country_part", "country_part", "country_part…
#> $ Code <chr> "AU1", "AU2", "AU3", "AU4", "AU5", "AU6", "AU…
#> $ Education <dbl> 8.0, 8.1, 7.8, 7.3, 7.6, 6.5, 8.1, 9.5, 8.8, …
#> $ Jobs <dbl> 8.1, 7.9, 8.1, 7.8, 8.8, 7.6, 8.7, 9.3, 7.8, …
#> $ Income <dbl> 6.8, 5.9, 6.3, 6.1, 7.9, 5.4, 8.2, 10.0, 5.7,…
#> $ Safety <dbl> 8.8, 9.5, 9.5, 9.0, 8.6, 8.8, 0.0, 10.0, 9.7,…
#> $ Health <dbl> 9.0, 9.5, 8.3, 8.5, 9.3, 5.4, 2.4, 9.3, 6.7, …
#> $ Environment <dbl> 9.8, 8.6, 9.9, 9.4, 9.6, 10.0, 9.2, 9.1, 3.5,…
#> $ Civic_engagement <dbl> 10.0, 10.0, 10.0, 10.0, 10.0, 10.0, 8.4, 10.0…
#> $ Accessiblity_to_services <dbl> 7.2, 7.5, 7.7, 7.2, 7.8, 6.8, 7.8, 8.7, 8.0, …
#> $ Housing <dbl> 7.2, 7.8, 8.3, 8.3, 8.9, 8.3, 5.6, 8.3, 6.1, …
#> $ Community <dbl> 8.9, 9.3, 8.6, 8.6, 8.5, 8.6, 10.0, 9.8, 8.3,…
#> $ Life_satisfaction <dbl> 7.8, 8.5, 8.1, 8.5, 7.8, 9.6, 7.0, 9.6, 7.8, …Wie glimpse() aufzeigt, liegen also einige qualitative (kategoriale, chr) und einige quantitative (metrische, dbl) Variablen vor. Die qualitativen Variablen sind für eine direkte Analyse weniger interessant; vielmehr ist es interessant, die Statistiken auf die Gruppen (Stufen, Level) der qualitativen Variablen aufzusplitten.
Betrachten wir aber zu Beginn die metrischen Variablen einzeln (univariat).
5 Metrische Variablen einzeln (univariat)
Die typischen Statistiken zu den metrischen Variablen liegen uns von inspect() bereits vor. Daher gehen wir weiter zur Visualisierung.
oecd %>%
ggplot(aes(x = Life_satisfaction)) +
geom_histogram()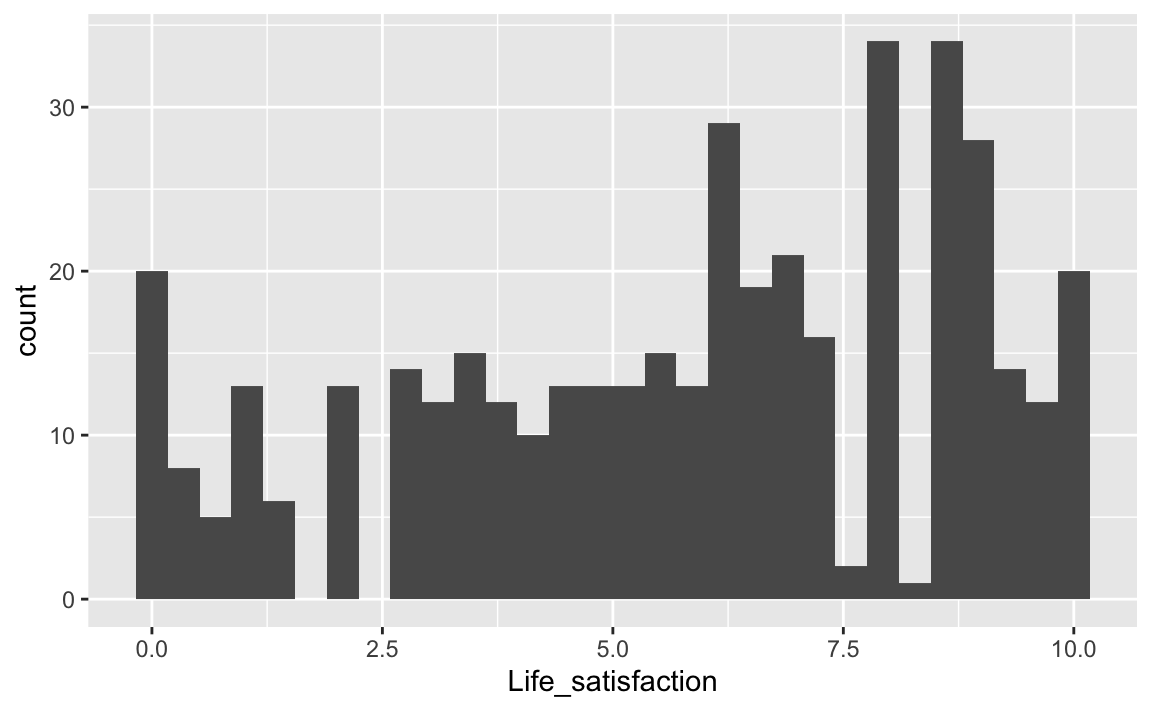
Eine ähnliche Aussage liefert das Dichte-Diagramm:
oecd %>%
ggplot(aes(x = Life_satisfaction)) +
geom_density()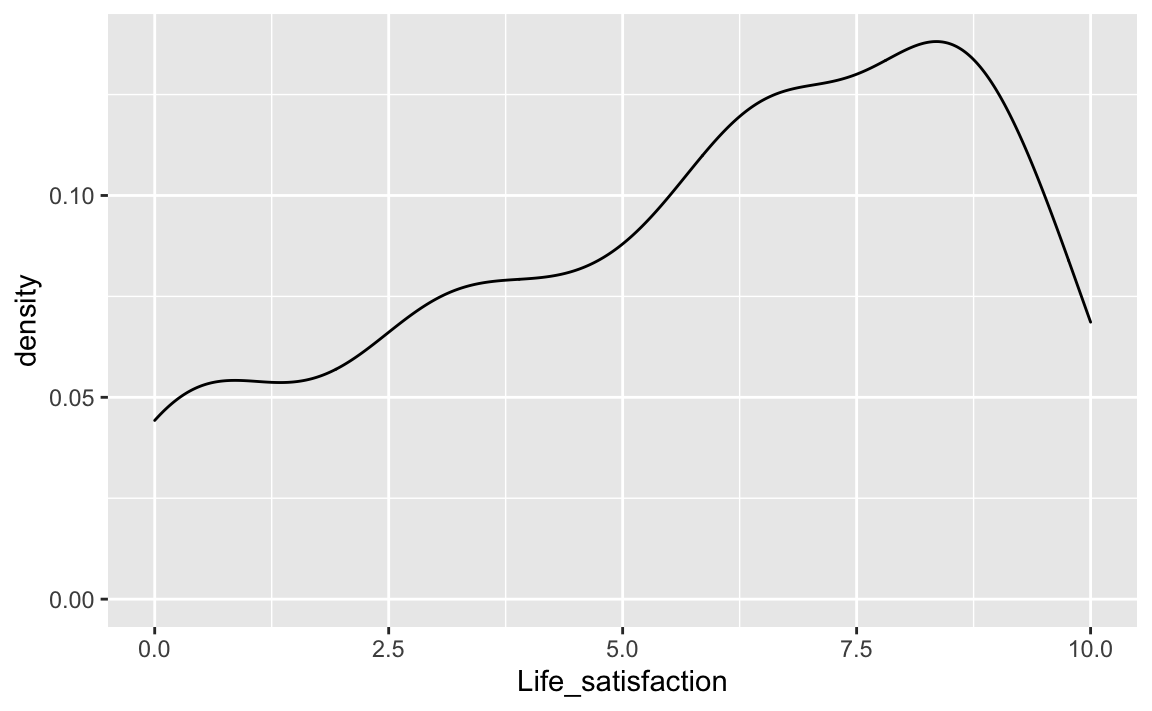
Die Dichte gibt an, welcher Anteil der Beobachtungen an der jeweiligen Stelle der X-Achse lägen, wenn man eine Einheit betrachtet (z.B. die Lebenszufriedenheit von 5-6).
5.1 Histogramm nach Gruppen
Angenommen, man möchte Deutschland mit Frankfreich vergleichen im Hinblick auf die Lebenszufriedenheit:
oecd %>%
filter(Country == "Germany" | Country == "France") -> oecd_de_frDann
oecd_de_fr %>%
ggplot(aes(x = Life_satisfaction)) +
geom_histogram(bins = 15) +
facet_wrap(~ Country)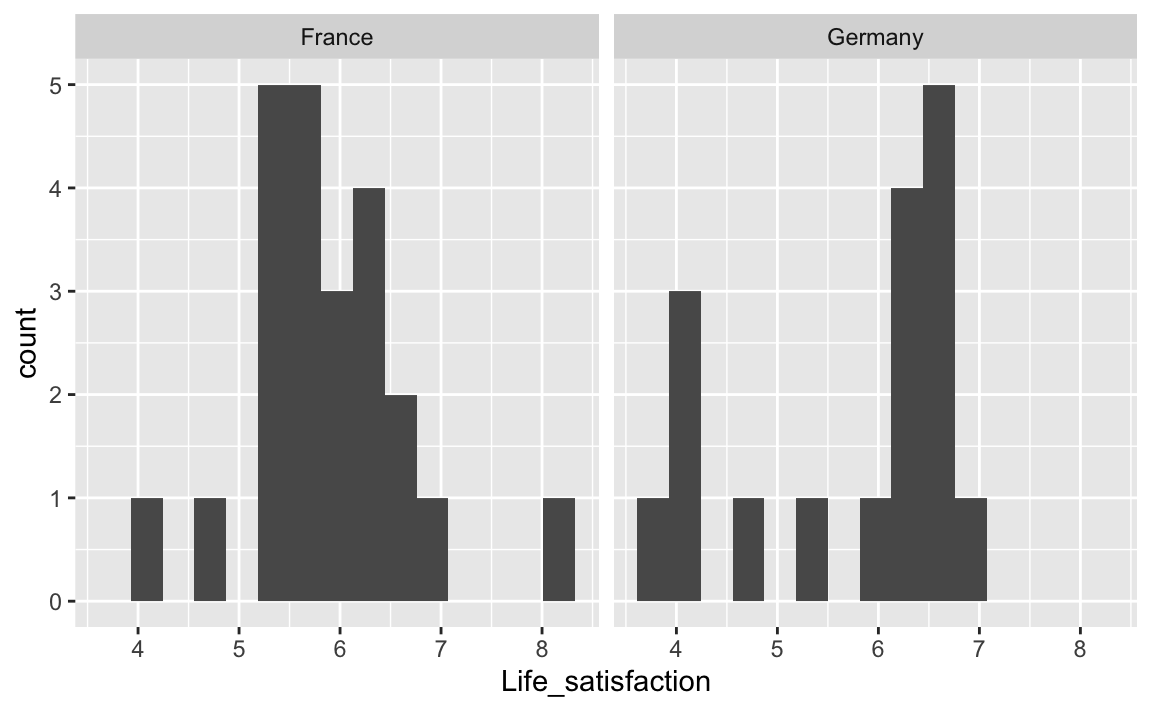
5.2 VERTIEFUNG: Histogramm für alle Variablen
Dieser Abschnitt ist eine Vertiefung; Sie können in überspringen, ohne den Anschluss zu den folgenden Abschnitten zu verlieren.
Um einen Überblick über die Verteilungen zu bekommen, bietet es sich an, sich alle anzuschauen. Das ist natürlich mit etwas Monotonie verbunden (den gleichen Befehl mehrfach wiederholen).
Malen wir einmal alle Histogramme auf einmal. Dazu brauchen wir ein weiteres Paket:
Als erstes erzeugen wir einen langen Dataframe (der nur aus metrischen Variablen besteht):
oecd_de_fr %>%
select(where(is.numeric)) %>% # wähle alle Spalten aus, wo sich Nummern finden
pivot_longer(everything()) %>% # baue alle Variablen in ein langes Format um
slice(1:10) # zeige die Zeilen 1 bis 10
#> # A tibble: 10 x 2
#> name value
#> <chr> <dbl>
#> 1 Education 7.8
#> 2 Jobs 6
#> 3 Income 6.3
#> 4 Safety 8.6
#> 5 Health 10
#> 6 Environment 3.5
#> 7 Civic_engagement 7.4
#> 8 Accessiblity_to_services 8.6
#> 9 Housing 3.3
#> 10 Community 7.9Dann plotten wir Histogramme, wobei wir nach den Ländern (key) gruppieren. Aber zuerst speichenr wir uns den “langen” Datensatz ab:
oecd_de_fr %>%
select(where(is.numeric)) %>% # wähle alle Spalten aus, wo sich Nummern finden
pivot_longer(everything()) -> oecd_de_fr_longBetrachten Sie diesen Daten einmal zur Übung.
Dann plotten wir in gewohnter Manier:
oecd_de_fr_long %>%
ggplot(aes(x = value)) +
geom_histogram() +
facet_wrap(~ name)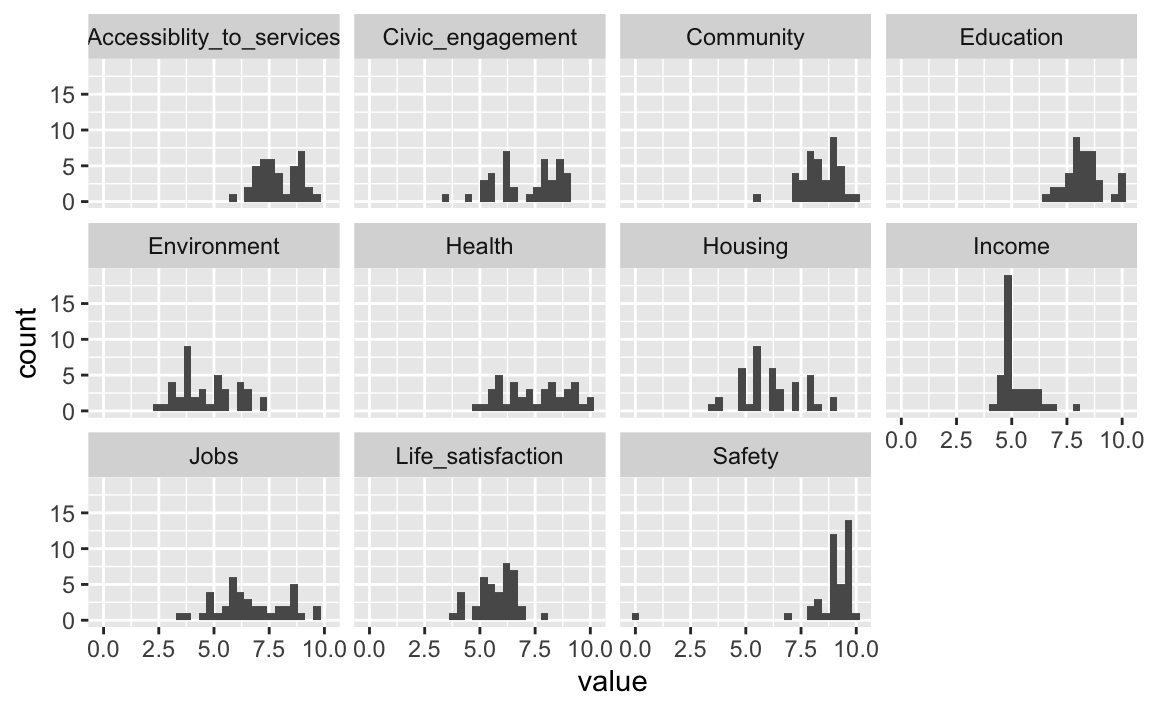
6 Forschungsfrage
Hat Deutschland in Vergleich zu anderen Ländern eine hohe Lebenszufriedenheit?
Die Frage ist noch recht unpräzise formuliert, aber dafür gibt sie Raum für eine Menge von Untersuchungsansätzen.
7 Datensatz filtern - nur Länder, keine Landesteile
Der Datensatz verstößt gegen die Regel, dass in jeder Zeile eine Beobachtungseinheit steht. In einigen Zeilen stehen Länder, in den meisten anderen aber Landesteile (wie Bayern, Baden-Württemberg etc.). Filtern wir uns nur die Länder, und exklduieren die Landesteile:
filter(oecd, region_type == "country_whole") -> oecd_shortDie Anzahl der Zeilen deses Datensatz oecd_short gibt uns Aufschluss über die Anzahl der untersuchten Länder.
8 Vergleich der Lebenszufriedenheit der Länder
oecd_short %>%
ggplot(aes(x = Country, y = Life_satisfaction)) +
geom_point()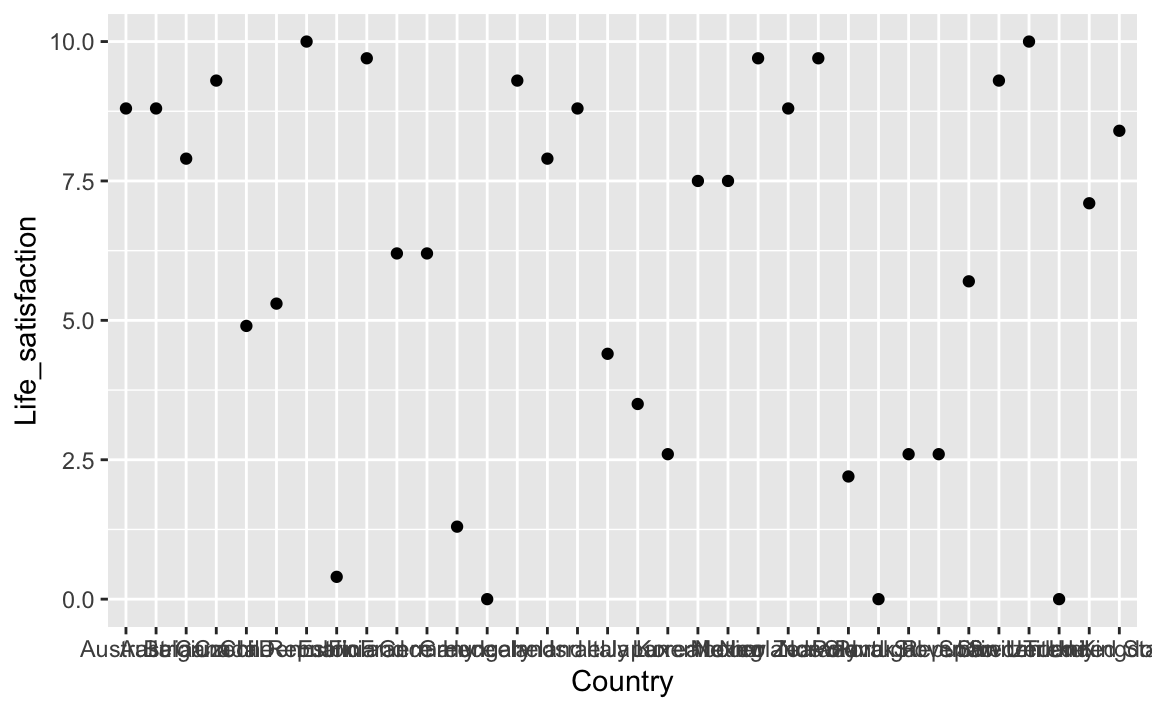
Hm, sieht nicht übersichtlich aus. Besser wäre es, die Punkte absteigend zu sortieren.
Betrachten wir dazu die Variable country näher: Es handelt sich um eine Character-Variable:
str(oecd)
#> spec_tbl_df[,15] [429 × 15] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
#> $ Country : chr [1:429] "Australia" "Australia" "Australia" "Australia" ...
#> $ Region : chr [1:429] "New South Wales" "Victoria" "Queensland" "South Australia" ...
#> $ region_type : chr [1:429] "country_part" "country_part" "country_part" "country_part" ...
#> $ Code : chr [1:429] "AU1" "AU2" "AU3" "AU4" ...
#> $ Education : num [1:429] 8 8.1 7.8 7.3 7.6 6.5 8.1 9.5 8.8 8.5 ...
#> $ Jobs : num [1:429] 8.1 7.9 8.1 7.8 8.8 7.6 8.7 9.3 7.8 8.2 ...
#> $ Income : num [1:429] 6.8 5.9 6.3 6.1 7.9 5.4 8.2 10 5.7 5.9 ...
#> $ Safety : num [1:429] 8.8 9.5 9.5 9 8.6 8.8 0 10 9.7 9.8 ...
#> $ Health : num [1:429] 9 9.5 8.3 8.5 9.3 5.4 2.4 9.3 6.7 6.6 ...
#> $ Environment : num [1:429] 9.8 8.6 9.9 9.4 9.6 10 9.2 9.1 3.5 2.6 ...
#> $ Civic_engagement : num [1:429] 10 10 10 10 10 10 8.4 10 8.6 8.1 ...
#> $ Accessiblity_to_services: num [1:429] 7.2 7.5 7.7 7.2 7.8 6.8 7.8 8.7 8 7.4 ...
#> $ Housing : num [1:429] 7.2 7.8 8.3 8.3 8.9 8.3 5.6 8.3 6.1 5.6 ...
#> $ Community : num [1:429] 8.9 9.3 8.6 8.6 8.5 8.6 10 9.8 8.3 7.8 ...
#> $ Life_satisfaction : num [1:429] 7.8 8.5 8.1 8.5 7.8 9.6 7 9.6 7.8 8.1 ...
#> - attr(*, "spec")=
#> .. cols(
#> .. Country = col_character(),
#> .. Region = col_character(),
#> .. region_type = col_character(),
#> .. Code = col_character(),
#> .. Education = col_double(),
#> .. Jobs = col_double(),
#> .. Income = col_double(),
#> .. Safety = col_double(),
#> .. Health = col_double(),
#> .. Environment = col_double(),
#> .. Civic_engagement = col_double(),
#> .. Accessiblity_to_services = col_double(),
#> .. Housing = col_double(),
#> .. Community = col_double(),
#> .. Life_satisfaction = col_double()
#> .. )Offensichtlich sind diese alphabetisch geordnet - nach dieser Ordnung richtet sich die Ordnung im Plot-Befehl (xyplot).
8.1 Umwandling in eine Faktor-Variable
In solchen Fällen bietet es sich an, die Character-Variable in eine Factor-Variable umzuwandeln; dann geht das Weitere einfacher.
oecd_short %>%
mutate(Country = factor(Country)) -> oecd_shortMöchte man wissen, wie viele unterschiedliche Werte eine Variable enthält, dann kann die Funktion distinct() verwenden:
oecd_short %>%
distinct(Country)
#> # A tibble: 34 x 1
#> Country
#> <fct>
#> 1 Australia
#> 2 Austria
#> 3 Belgium
#> 4 Canada
#> 5 Chile
#> 6 Czech Republic
#> 7 Denmark
#> 8 Estonia
#> 9 Finland
#> 10 France
#> # … with 24 more rows8.2 Ranking und Top-10-Prozent der Zufriedenheit
Schauen wir uns die “Happy-Top-10” an, die 10 Länder mit der höchsten Lebenszufriedenheit:
oecd_short %>%
arrange(-Life_satisfaction) %>%
select(Country, Life_satisfaction) %>%
slice(1:10)
#> # A tibble: 10 x 2
#> Country Life_satisfaction
#> <fct> <dbl>
#> 1 Denmark 10
#> 2 Switzerland 10
#> 3 Finland 9.7
#> 4 Netherlands 9.7
#> 5 Norway 9.7
#> 6 Canada 9.3
#> 7 Iceland 9.3
#> 8 Sweden 9.3
#> 9 Australia 8.8
#> 10 Austria 8.8Mit welcher Lebenszufriedenheit gehört ein Land zu den Top-10-Prozent der zufriedenen Länder?
oecd_short %>%
summarise(quantile(Life_satisfaction, probs = .90))
#> # A tibble: 1 x 1
#> `quantile(Life_satisfaction, probs = 0.9)`
#> <dbl>
#> 1 9.7Ah, Länder mit einer Lebenszufriedenheit von mind. 9.7 gehören zu den oberen Top-10-Prozent. Filtern wir mal entsprechend:
oecd_short %>%
filter(Life_satisfaction >= 9.7) %>%
select(Country, Life_satisfaction)
#> # A tibble: 5 x 2
#> Country Life_satisfaction
#> <fct> <dbl>
#> 1 Denmark 10
#> 2 Finland 9.7
#> 3 Netherlands 9.7
#> 4 Norway 9.7
#> 5 Switzerland 108.3 Vertiefung
Ändern wir die Sortierung! Mit reorder() kann man die Sortierung ändern (re-ordnen, daher der Name):
oecd_short %>%
mutate(Country_sorted = reorder(Country, Life_satisfaction)) -> oecd_short_reorderedIst das jetzt geordnet? str() verrät es uns:
str(oecd_short_reordered)
#> spec_tbl_df[,16] [34 × 16] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
#> $ Country : Factor w/ 34 levels "Australia","Austria",..: 1 2 3 4 5 6 7 8 9 10 ...
#> $ Region : chr [1:34] "Australia" "Austria" "Belgium" "Canada" ...
#> $ region_type : chr [1:34] "country_whole" "country_whole" "country_whole" "country_whole" ...
#> $ Code : chr [1:34] "AUS" "AUT" "BEL" "CAN" ...
#> $ Education : num [1:34] 7.6 8.4 7.5 9.2 7.2 10 6.7 9.6 8.7 7.6 ...
#> $ Jobs : num [1:34] 7.9 7.7 5 6.6 6.2 7.3 7.9 6.6 6.4 5.2 ...
#> $ Income : num [1:34] 9.5 7.9 6.2 7.4 0.4 2.8 5.1 1 5.6 7 ...
#> $ Safety : num [1:34] 8.4 10 5.7 6.5 0.6 6.1 10 0 10 8.4 ...
#> $ Health : num [1:34] 9 7.2 6.6 8.5 4.2 2.7 5.8 2.1 7.3 9.3 ...
#> $ Environment : num [1:34] 9.7 2.8 1.9 7.4 8.5 1.4 5.8 6.4 7.9 4.5 ...
#> $ Civic_engagement : num [1:34] 10 6.2 9.7 4.7 0.1 2.6 8.9 3.7 4.8 7.5 ...
#> $ Accessiblity_to_services: num [1:34] 6.9 7.2 7.6 8.1 0 6.7 8.3 7.6 9 6.9 ...
#> $ Housing : num [1:34] 9.5 5.1 8.8 10 1.5 2.9 6.6 1.5 6.6 5.1 ...
#> $ Community : num [1:34] 8.8 7.6 7.7 8.5 2.5 5.1 9.6 4.6 8.7 7.6 ...
#> $ Life_satisfaction : num [1:34] 8.8 8.8 7.9 9.3 4.9 5.3 10 0.4 9.7 6.2 ...
#> $ Country_sorted : Factor w/ 34 levels "Hungary","Portugal",..: 23 24 20 27 12 13 33 4 30 15 ...
#> ..- attr(*, "scores")= num [1:34(1d)] 8.8 8.8 7.9 9.3 4.9 5.3 10 0.4 9.7 6.2 ...
#> .. ..- attr(*, "dimnames")=List of 1
#> .. .. ..$ : chr [1:34] "Australia" "Austria" "Belgium" "Canada" ...
#> - attr(*, "spec")=
#> .. cols(
#> .. Country = col_character(),
#> .. Region = col_character(),
#> .. region_type = col_character(),
#> .. Code = col_character(),
#> .. Education = col_double(),
#> .. Jobs = col_double(),
#> .. Income = col_double(),
#> .. Safety = col_double(),
#> .. Health = col_double(),
#> .. Environment = col_double(),
#> .. Civic_engagement = col_double(),
#> .. Accessiblity_to_services = col_double(),
#> .. Housing = col_double(),
#> .. Community = col_double(),
#> .. Life_satisfaction = col_double()
#> .. )Wie man sieht, ist Country_sorted jetzt anders sortiert. Betrachten wir das Ergebnis:
plot_sorted <- oecd_short_reordered %>%
ggplot(aes(x = Country_sorted, y = Life_satisfaction)) +
geom_point()
plot_sorted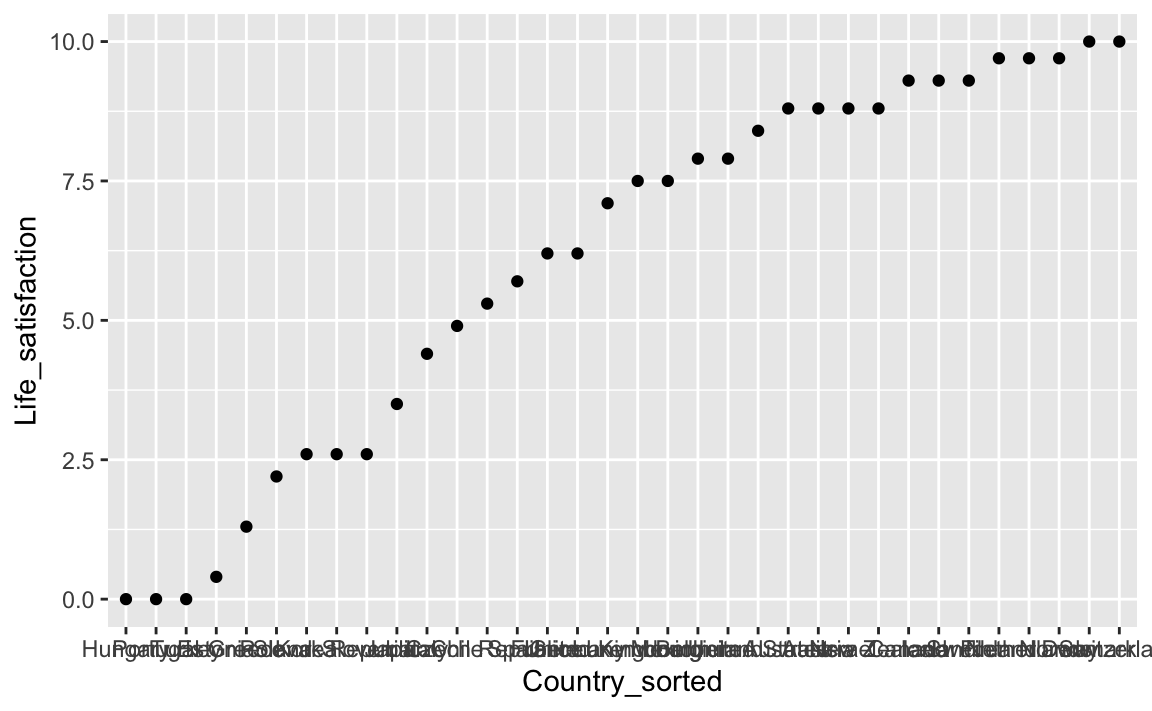
Schon besser. Man kann z.B. die Achsen nicht lesen 😞. Was könnte man da bloß tun?
8.4 Vertiefung
Mit + coord_flip() lassen sich die Achsen um 90 Grad drehen:
plot_sorted + coord_flip()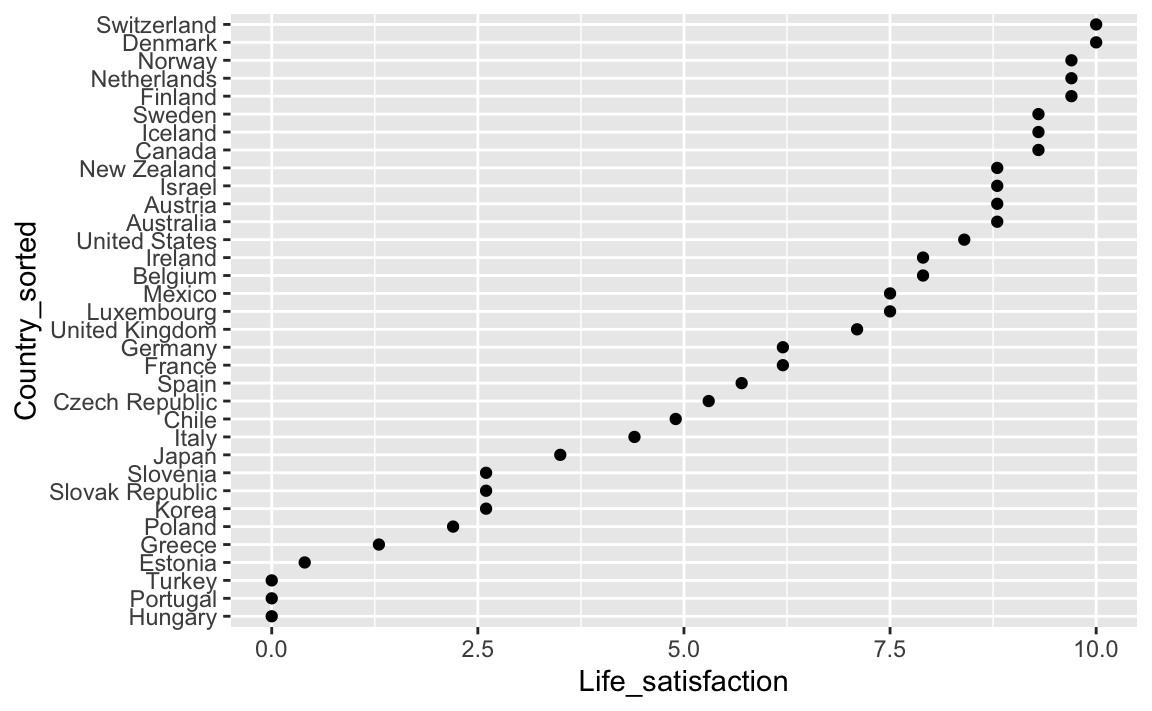
Schön 😄.
Man hätte das Sortieren und Achsen drehen auch in einem Haps machen können:
oecd_short_reordered %>%
ggplot(aes(x = Country_sorted, y = Life_satisfaction)) +
geom_point() + coord_flip()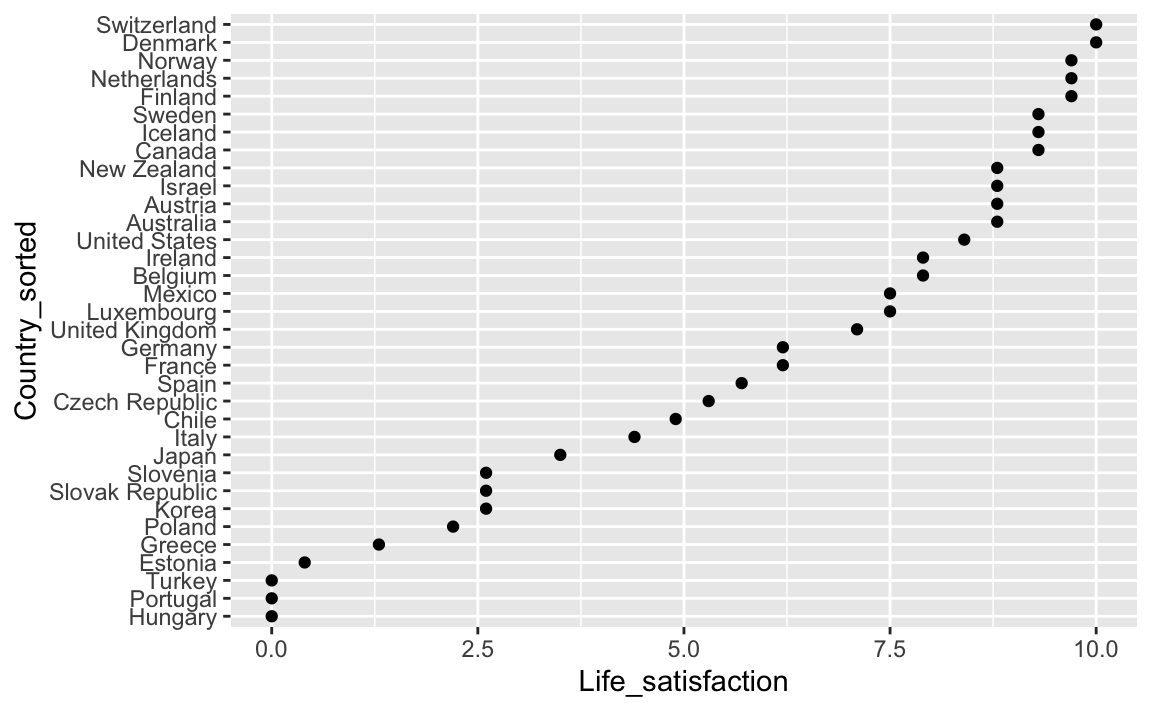
Aber übersichtliches ist es, die Dinge nacheinander zu tun.
8.5 Vertiefung
Schön wäre es noch, im Bild den Mittelwert o.Ä. zu sehen:
oecd_short_reordered %>%
ggplot(aes(x = Country_sorted, y = Life_satisfaction)) +
geom_point() +
geom_hline(yintercept = 6.08, data = NA, color = "firebrick") +
coord_flip()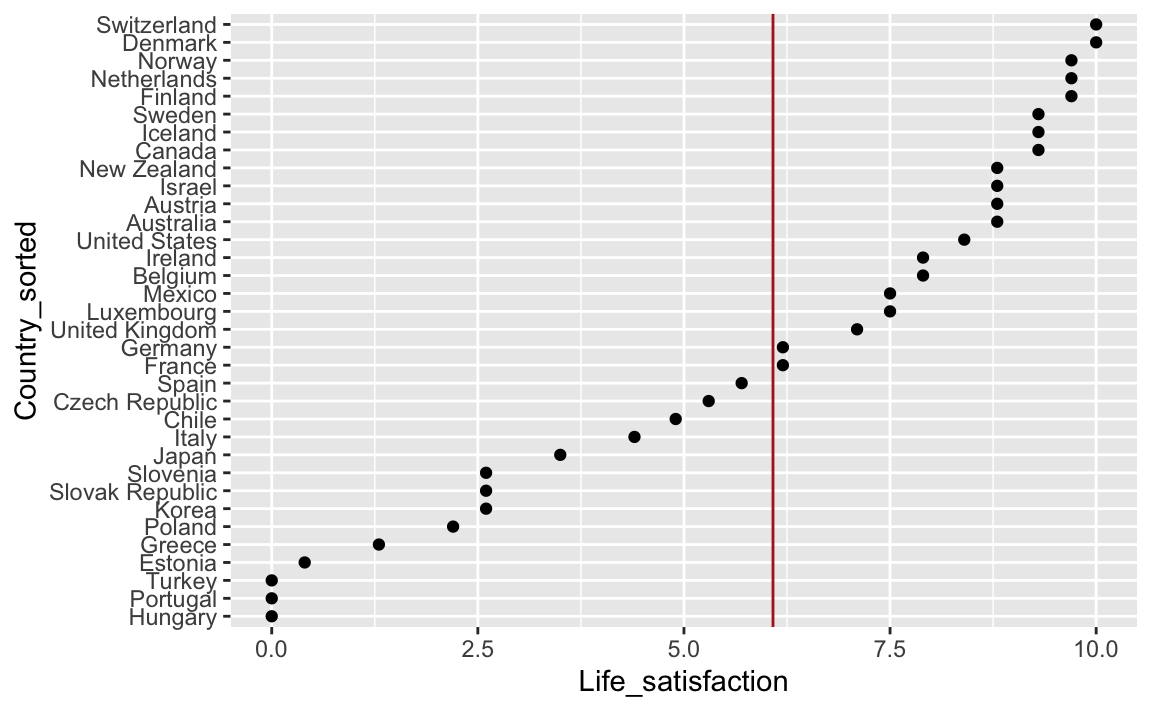
Tja, die Wünsche hören nie auf… Wäre es nicht noch nett, wenn “Deutschland” hervorgehoben wäre, optisch, so dass es im Diagramm hervorsticht. Nehmen wir an, wir sind an diesem Land besonders interessiert.
oecd_short_reordered <-
oecd_short_reordered %>%
mutate(is_Germany = Country == "Germany")Damit haben wir eine Spalte erstellt, die angibt, ob ein Land Deutschland ist (TRUE) oder nicht (FALSE). Diese neue Variable nehmen wir her, um die Farbe, Größe und Form der Punkte zu bestimmen:
oecd_short_reordered %>%
ggplot(aes(x = Country_sorted, y = Life_satisfaction)) +
geom_point(aes(color = is_Germany, shape = is_Germany, size = is_Germany)) +
geom_hline(yintercept = 6.08, data = NA, color = "firebrick") +
geom_hline(yintercept = 6.08, data = NA, color = "grey60") %>%
geom_vline(xintercept = 16, data = NA, color = "grey80") +
coord_flip()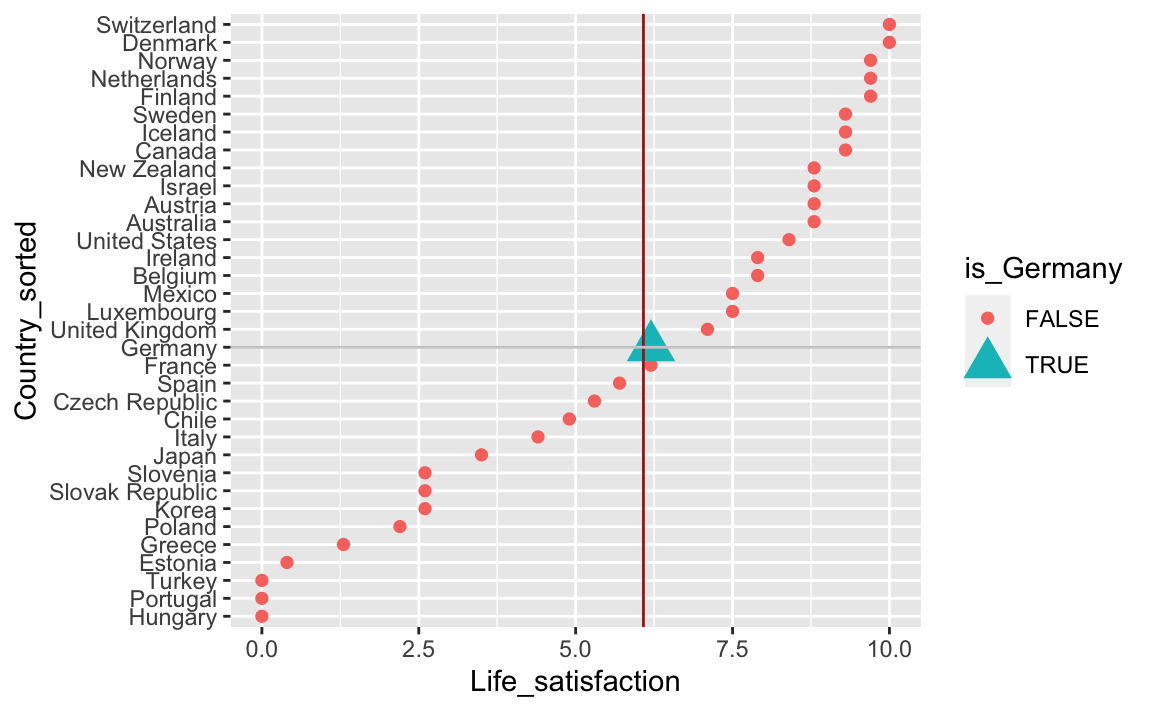
9 Zusammenhang zweier metrischer Variablen – Punktediagramm
Hängt die Lebenszufriedenheit mit Civic_engagment zusammen?
oecd_short_reordered %>%
ggplot(aes(x = Civic_engagement, y = Life_satisfaction)) +
geom_point()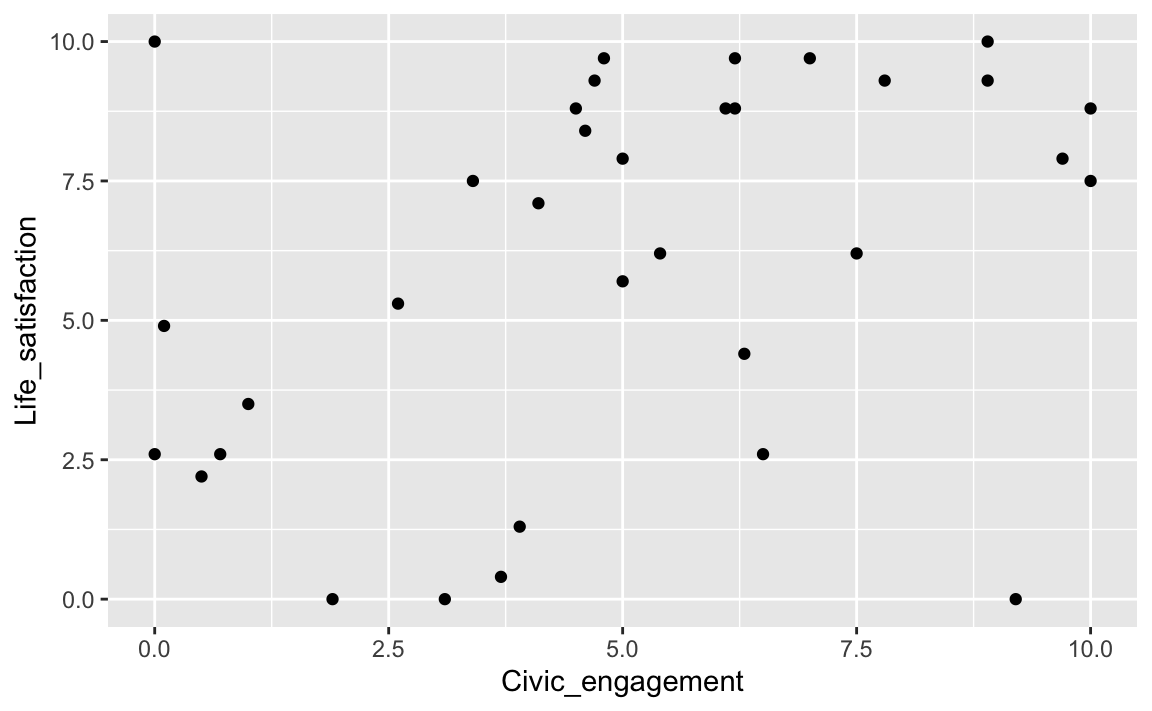
Hm, es ist kein starker Trend zu erkennen.
Was sagt die Korrelation dazu:
oecd_short_reordered %>%
summarise(cor_ce_ls = cor(Civic_engagement, Life_satisfaction))
#> # A tibble: 1 x 1
#> cor_ce_ls
#> <dbl>
#> 1 0.402Immerhin, kein ganz unwesentlicher Wert.
9.0.1 Und so weiter
Dieses Prinzip mit dem Punktediagramm könnte man jetzt weiterführen ad nauseam.
9.1 Vertiefung Pairs plot
Eleganter geht es so. Dafür benötigen wir Extra-Pakete:
library(sjPlot)Dann erstellen wir einen Dataframe mit nur metrischen Variablen; d.h. wir entfernen die nicht-metrischen Variablen:
oecd_short_reordered %>%
select(-Country, -Region, -region_type, -Code, -Country_sorted) -> oecd_short_numericÜbrigens kann (und muss man oft) mehrere Werte mit dem Befehl c() zusammenfassen (c wie “combine”):
oecd_short_reordered %>%
select(-c(Country, Region, region_type, Code, Country_sorted)) -> oecd_short_numericOder man wählt gleich nur die numerischen Variablen aus:
oecd_short_reordered %>%
select(where(is.numeric)) -> oecd_short_numericsjp.corr(oecd_short_numeric)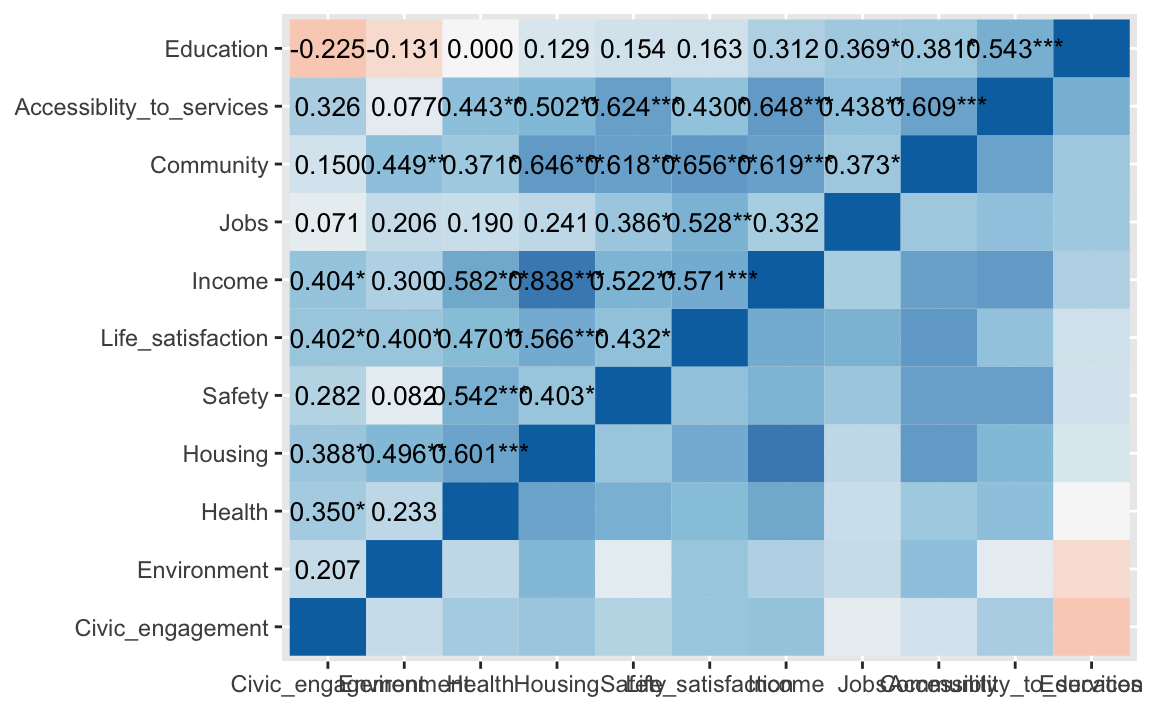
9.1.1 Vertiefung ggpairs
library(GGally)Das sieht auch ganz nett aus:
ggpairs(oecd_short,
columns = c(5,6,7,15))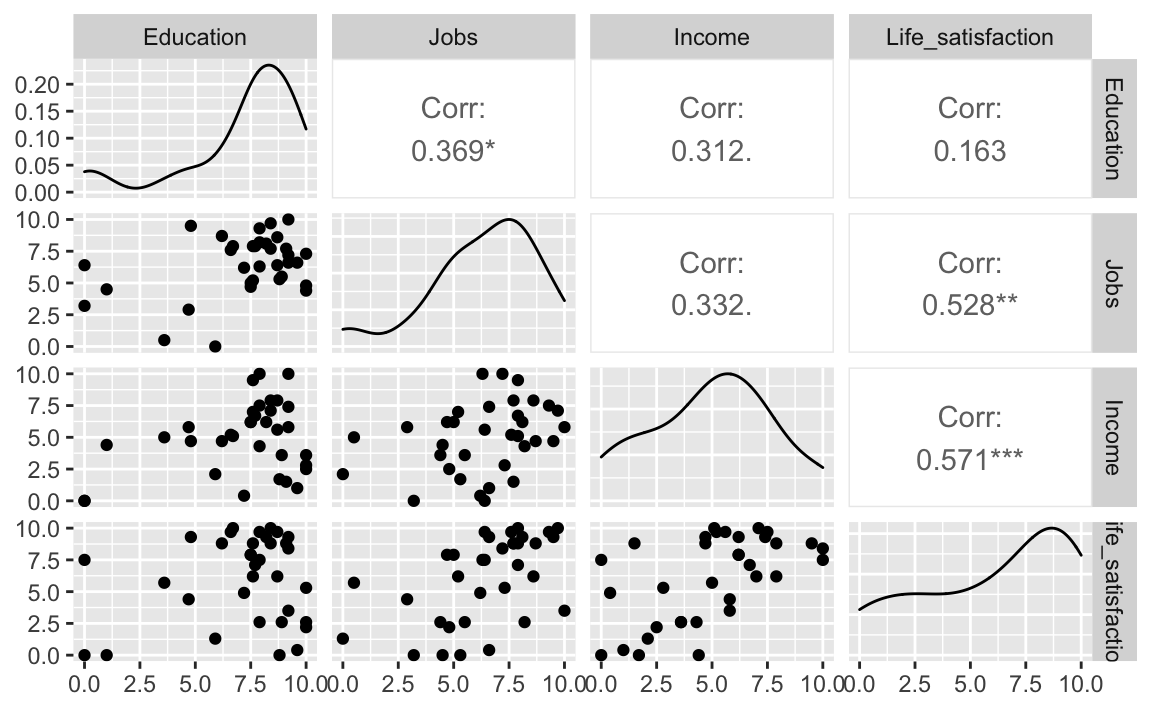
9.2 Zusammenhang zweier Variablen unter Berücksichtigung von Drittvariablen
Oben haben wir gesehen, dass Lebenszufriedenheit und Civiv Engagement zusammenhängen.
Aber vielleicht hängt dieser Zusammenhang wiederum von der finanziellen Absicherung ab? Nur wenn man materiell abgesichert ist, so könnte man argumentieren, wird bürgerliches Engagement (bzw. die Möglichkeit zu) eine Einflussgröße auf die Lebenszufriedenheit.
Um diese Frage zu untersuchen, teilen wir Income in zwei Stufen, hoch und gering. Dann untersuchen wir jeweils den Zusammenhang von Lebenszufriedenheit und bürgerlichem Engagement.
Achtung! Eine metrische Variablen in zwei Hälften zu spalten birgt einen hohen Informationsverlust. Da wir aber nur eine grobe Untersuchung vorhaben (und uns noch nicht fortgeschrittener Technik bedienen wollen), bleiben wir erstmal bei dieser sog. Dichotomisierung.
Nehmen wir den Median des Einkommen als Teilungspunkt; man spricht von einem “Mediansplit”:
oecd_short %>%
summarise(Income_md = median(Income))
#> # A tibble: 1 x 1
#> Income_md
#> <dbl>
#> 1 5.15Zuerst erstellen wir eine Variable Income_high mit den Stufen 0 (nein) und 1 (ja):
oecd_short_reordered <-
oecd_short_reordered %>%
mutate(Income_high =
case_when( Income >= 5.15 ~ 1,
Income < 5.15 ~ 0))Jetzt plotten wir den Zusammenhang:
income_labels <- c(`0` = "arm",
`1` ="reich")
oecd_short_reordered %>%
ggplot(aes(x = Country_sorted, y = Life_satisfaction)) +
geom_point() +
facet_wrap(~ Income_high,
labeller = labeller(Income_high = income_labels)) +
coord_flip() +
labs(y = "Länder",
x = "Lebenszufriedenheit",
title = "Lebenszufriedenheit in armen und reichen Ländern ") +
theme_minimal()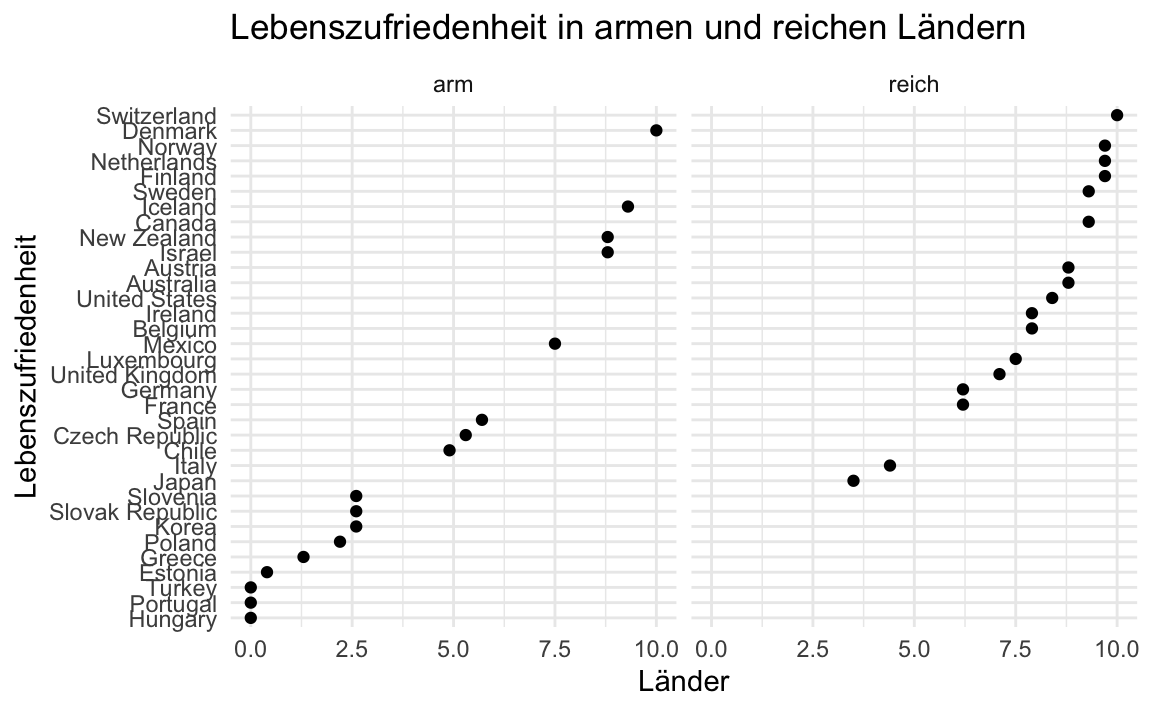
9.2.1 Vertiefung: Korrelation pro Gruppe
Um die Korrelation pro Gruppe zu erhalten, könnten wir jeweils einen Dataframe pro Gruppe erzeugen (mit filter()) und dann jeweils die Korrelation von Zufriedenheit und Engagement berechnen.
Eine andere, etwas elegantere Möglichkeit kann so aussehen:
oecd_short_reordered %>%
group_by(Income_high) %>%
summarise(cor_zuf_eng = cor(Life_satisfaction, Civic_engagement))
#> # A tibble: 2 x 2
#> Income_high cor_zuf_eng
#> <dbl> <dbl>
#> 1 0 0.367
#> 2 1 0.140Interessanterweise ist die Korrelation durchaus verschieden in den beiden Gruppen.
Natürlich sind die beiden Gruppen nur Stichproben - es stellt sich die Frage, ob die Unterschiede nur durch Zufälligkeiten des Stichprobenziehens entstanden sind oder auch in der Grundgesatmtheit der “reichen” und “armen” Ländern existieren? Dazu später mehr!
10 Deskriptive Statistiken nach Ländern
10.1 Lebenszufriedenheit
Das ist relativ einfach:
oecd_short_reordered %>%
select(Life_satisfaction) %>%
skim()| Name | Piped data |
| Number of rows | 34 |
| Number of columns | 1 |
| _______________________ | |
| Column type frequency: | |
| numeric | 1 |
| ________________________ | |
| Group variables | None |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| Life_satisfaction | 0 | 1 | 6.07 | 3.38 | 0 | 2.83 | 7.3 | 8.8 | 10 | ▃▃▂▅▇ |
11 Reproducibility
#> ─ Session info ───────────────────────────────────────────────────────────────────────────────────────────────────────
#> setting value
#> version R version 4.0.2 (2020-06-22)
#> os macOS 10.16
#> system x86_64, darwin17.0
#> ui X11
#> language (EN)
#> collate en_US.UTF-8
#> ctype en_US.UTF-8
#> tz Europe/Berlin
#> date 2021-02-11
#>
#> ─ Packages ───────────────────────────────────────────────────────────────────────────────────────────────────────────
#> package * version date lib source
#> assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.0.0)
#> backports 1.2.1 2020-12-09 [1] CRAN (R 4.0.2)
#> blogdown 1.1 2021-01-19 [1] CRAN (R 4.0.2)
#> bookdown 0.21.6 2021-02-02 [1] Github (rstudio/bookdown@6c7346a)
#> broom 0.7.4 2021-01-29 [1] CRAN (R 4.0.2)
#> bslib 0.2.4.9000 2021-02-02 [1] Github (rstudio/bslib@b3cd7a9)
#> cachem 1.0.1 2021-01-21 [1] CRAN (R 4.0.2)
#> callr 3.5.1 2020-10-13 [1] CRAN (R 4.0.2)
#> cellranger 1.1.0 2016-07-27 [1] CRAN (R 4.0.0)
#> cli 2.3.0 2021-01-31 [1] CRAN (R 4.0.2)
#> codetools 0.2-16 2018-12-24 [2] CRAN (R 4.0.2)
#> colorspace 2.0-0 2020-11-11 [1] CRAN (R 4.0.2)
#> crayon 1.4.1 2021-02-08 [1] CRAN (R 4.0.2)
#> DBI 1.1.1 2021-01-15 [1] CRAN (R 4.0.2)
#> dbplyr 2.0.0 2020-11-03 [1] CRAN (R 4.0.2)
#> desc 1.2.0 2018-05-01 [1] CRAN (R 4.0.0)
#> devtools 2.3.2 2020-09-18 [1] CRAN (R 4.0.2)
#> digest 0.6.27 2020-10-24 [1] CRAN (R 4.0.2)
#> dplyr * 1.0.3 2021-01-15 [1] CRAN (R 4.0.2)
#> ellipsis 0.3.1 2020-05-15 [1] CRAN (R 4.0.0)
#> evaluate 0.14 2019-05-28 [1] CRAN (R 4.0.0)
#> fastmap 1.1.0 2021-01-25 [1] CRAN (R 4.0.2)
#> forcats * 0.5.1 2021-01-27 [1] CRAN (R 4.0.2)
#> fs 1.5.0 2020-07-31 [1] CRAN (R 4.0.2)
#> generics 0.1.0 2020-10-31 [1] CRAN (R 4.0.2)
#> ggplot2 * 3.3.3 2020-12-30 [1] CRAN (R 4.0.2)
#> glue 1.4.2 2020-08-27 [1] CRAN (R 4.0.2)
#> gtable 0.3.0 2019-03-25 [1] CRAN (R 4.0.0)
#> haven 2.3.1 2020-06-01 [1] CRAN (R 4.0.0)
#> hms 1.0.0 2021-01-13 [1] CRAN (R 4.0.2)
#> htmltools 0.5.1.1 2021-01-22 [1] CRAN (R 4.0.2)
#> httr 1.4.2 2020-07-20 [1] CRAN (R 4.0.2)
#> jquerylib 0.1.3 2020-12-17 [1] CRAN (R 4.0.2)
#> jsonlite 1.7.2 2020-12-09 [1] CRAN (R 4.0.2)
#> knitr 1.31 2021-01-27 [1] CRAN (R 4.0.2)
#> lifecycle 0.2.0 2020-03-06 [1] CRAN (R 4.0.0)
#> lubridate 1.7.9.2 2020-11-13 [1] CRAN (R 4.0.2)
#> magrittr 2.0.1 2020-11-17 [1] CRAN (R 4.0.2)
#> memoise 2.0.0 2021-01-26 [1] CRAN (R 4.0.2)
#> modelr 0.1.8 2020-05-19 [1] CRAN (R 4.0.0)
#> munsell 0.5.0 2018-06-12 [1] CRAN (R 4.0.0)
#> pillar 1.4.7 2020-11-20 [1] CRAN (R 4.0.2)
#> pkgbuild 1.2.0 2020-12-15 [1] CRAN (R 4.0.2)
#> pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.0.0)
#> pkgload 1.1.0 2020-05-29 [1] CRAN (R 4.0.0)
#> prettyunits 1.1.1 2020-01-24 [1] CRAN (R 4.0.0)
#> processx 3.4.5 2020-11-30 [1] CRAN (R 4.0.2)
#> ps 1.5.0 2020-12-05 [1] CRAN (R 4.0.2)
#> purrr * 0.3.4 2020-04-17 [1] CRAN (R 4.0.0)
#> R6 2.5.0 2020-10-28 [1] CRAN (R 4.0.2)
#> Rcpp 1.0.6 2021-01-15 [1] CRAN (R 4.0.2)
#> readr * 1.4.0 2020-10-05 [1] CRAN (R 4.0.2)
#> readxl 1.3.1 2019-03-13 [1] CRAN (R 4.0.0)
#> remotes 2.2.0 2020-07-21 [1] CRAN (R 4.0.2)
#> reprex 1.0.0 2021-01-27 [1] CRAN (R 4.0.2)
#> rlang 0.4.10 2020-12-30 [1] CRAN (R 4.0.2)
#> rmarkdown 2.6.6 2021-02-11 [1] Github (rstudio/rmarkdown@a62cb20)
#> rprojroot 2.0.2 2020-11-15 [1] CRAN (R 4.0.2)
#> rstudioapi 0.13.0-9000 2021-02-11 [1] Github (rstudio/rstudioapi@9d21f50)
#> rvest 0.3.6 2020-07-25 [1] CRAN (R 4.0.2)
#> sass 0.3.1 2021-01-24 [1] CRAN (R 4.0.2)
#> scales 1.1.1 2020-05-11 [1] CRAN (R 4.0.0)
#> sessioninfo 1.1.1 2018-11-05 [1] CRAN (R 4.0.0)
#> stringi 1.5.3 2020-09-09 [1] CRAN (R 4.0.2)
#> stringr * 1.4.0 2019-02-10 [1] CRAN (R 4.0.0)
#> testthat 3.0.1 2020-12-17 [1] CRAN (R 4.0.2)
#> tibble * 3.0.6 2021-01-29 [1] CRAN (R 4.0.2)
#> tidyr * 1.1.2 2020-08-27 [1] CRAN (R 4.0.2)
#> tidyselect 1.1.0 2020-05-11 [1] CRAN (R 4.0.0)
#> tidyverse * 1.3.0 2019-11-21 [1] CRAN (R 4.0.0)
#> usethis 2.0.0 2020-12-10 [1] CRAN (R 4.0.2)
#> vctrs 0.3.6 2020-12-17 [1] CRAN (R 4.0.2)
#> withr 2.4.1 2021-01-26 [1] CRAN (R 4.0.2)
#> xfun 0.21 2021-02-10 [1] CRAN (R 4.0.2)
#> xml2 1.3.2 2020-04-23 [1] CRAN (R 4.0.0)
#> yaml 2.2.1 2020-02-01 [1] CRAN (R 4.0.0)
#>
#> [1] /Users/sebastiansaueruser/Rlibs
#> [2] /Library/Frameworks/R.framework/Versions/4.0/Resources/library