1 Hintergrund
Diese Übung bezieht sich auf ISRS, Kap. 6.2.
2 Achtung
Gelman hasst schrittweise Regression …
3 Pakete
library(tidyverse) # data wrangling
library(broom) # tidy Regressionsoutput
library(skimr) # EDA
library(moderndive) # Komfort
library(olsrr) # Schrittweise Regression4 Daten laden
Auf dieser Seite sind die Daten zu finden.
d <- read_csv("https://www.openintro.org/data/csv/mariokart.csv")(“d” wie Daten.)
Wir werfen einen Blick in die Daten:
glimpse(d)
#> Rows: 143
#> Columns: 12
#> $ id <dbl> 150377422259, 260483376854, 320432342985, 280405224677, 1…
#> $ duration <dbl> 3, 7, 3, 3, 1, 3, 1, 1, 3, 7, 1, 1, 1, 1, 7, 7, 3, 3, 1, …
#> $ n_bids <dbl> 20, 13, 16, 18, 20, 19, 13, 15, 29, 8, 15, 15, 13, 16, 6,…
#> $ cond <chr> "new", "used", "new", "new", "new", "new", "used", "new",…
#> $ start_pr <dbl> 0.99, 0.99, 0.99, 0.99, 0.01, 0.99, 0.01, 1.00, 0.99, 19.…
#> $ ship_pr <dbl> 4.00, 3.99, 3.50, 0.00, 0.00, 4.00, 0.00, 2.99, 4.00, 4.0…
#> $ total_pr <dbl> 51.55, 37.04, 45.50, 44.00, 71.00, 45.00, 37.02, 53.99, 4…
#> $ ship_sp <chr> "standard", "firstClass", "firstClass", "standard", "medi…
#> $ seller_rate <dbl> 1580, 365, 998, 7, 820, 270144, 7284, 4858, 27, 201, 4858…
#> $ stock_photo <chr> "yes", "yes", "no", "yes", "yes", "yes", "yes", "yes", "y…
#> $ wheels <dbl> 1, 1, 1, 1, 2, 0, 0, 2, 1, 1, 2, 2, 2, 2, 1, 0, 1, 1, 2, …
#> $ title <chr> "~~ Wii MARIO KART & WHEEL ~ NINTENDO Wii ~ BRAND NEW…Oder lieber so:
skim(d)| Name | d |
| Number of rows | 143 |
| Number of columns | 12 |
| _______________________ | |
| Column type frequency: | |
| character | 4 |
| numeric | 8 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| cond | 0 | 1.00 | 3 | 4 | 0 | 2 | 0 |
| ship_sp | 0 | 1.00 | 5 | 10 | 0 | 8 | 0 |
| stock_photo | 0 | 1.00 | 2 | 3 | 0 | 2 | 0 |
| title | 1 | 0.99 | 13 | 59 | 0 | 80 | 0 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| id | 0 | 1 | 2.235290e+11 | 8.809543e+10 | 1.104392e+11 | 1.403506e+11 | 2.204911e+11 | 2.953551e+11 | 4.000775e+11 | ▇▃▅▅▃ |
| duration | 0 | 1 | 3.770000e+00 | 2.590000e+00 | 1.000000e+00 | 1.000000e+00 | 3.000000e+00 | 7.000000e+00 | 1.000000e+01 | ▇▅▂▆▁ |
| n_bids | 0 | 1 | 1.354000e+01 | 5.880000e+00 | 1.000000e+00 | 1.000000e+01 | 1.400000e+01 | 1.700000e+01 | 2.900000e+01 | ▂▅▇▃▁ |
| start_pr | 0 | 1 | 8.780000e+00 | 1.507000e+01 | 1.000000e-02 | 9.900000e-01 | 1.000000e+00 | 1.000000e+01 | 6.995000e+01 | ▇▁▁▁▁ |
| ship_pr | 0 | 1 | 3.140000e+00 | 3.210000e+00 | 0.000000e+00 | 0.000000e+00 | 3.000000e+00 | 4.000000e+00 | 2.551000e+01 | ▇▁▁▁▁ |
| total_pr | 0 | 1 | 4.988000e+01 | 2.569000e+01 | 2.898000e+01 | 4.117000e+01 | 4.650000e+01 | 5.399000e+01 | 3.265100e+02 | ▇▁▁▁▁ |
| seller_rate | 0 | 1 | 1.589842e+04 | 5.184032e+04 | 0.000000e+00 | 1.090000e+02 | 8.200000e+02 | 4.858000e+03 | 2.701440e+05 | ▇▁▁▁▁ |
| wheels | 0 | 1 | 1.150000e+00 | 8.500000e-01 | 0.000000e+00 | 0.000000e+00 | 1.000000e+00 | 2.000000e+00 | 4.000000e+00 | ▆▇▇▁▁ |
5 Fehlende Werte
Fehlende Werte können Probleme bereiten. Entfernen wir einfach alle fehlenden Werte, es sind ja nicht so viele.
d_nona <- d %>% # nona wie "no NA", keine fehlenden Werte
drop_na()6 Modell 0
lm0 <- lm(total_pr ~ 1, data = d_nona)Wie ist das R-Quadrat?
summary(lm0)
#>
#> Call:
#> lm(formula = total_pr ~ 1, data = d_nona)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -20.903 -8.796 -3.618 4.107 276.627
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 49.883 2.163 23.06 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 25.78 on 141 degrees of freedomOder so:
lm0_guete <- glance(lm0)
lm0_guete
#> # A tibble: 1 x 12
#> r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
#> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 0 0 25.8 NA NA NA -662. 1329. 1335.
#> # … with 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>Nur das adj.r.squared:
lm0_guete %>%
select(adj.r.squared)
#> # A tibble: 1 x 1
#> adj.r.squared
#> <dbl>
#> 1 07 Modelle mit einer Variablen (lm1)
Jetzt probieren wir alle Prädiktoren aus, um zu sehen, welche zum höchsten \(R^2\)-Wert führt.
7.1 lm1a
lm1a <- lm(total_pr ~ duration, data = d_nona)glance(lm1a) %>%
select(adj.r.squared)
#> # A tibble: 1 x 1
#> adj.r.squared
#> <dbl>
#> 1 -0.005437.2 lm1b
lm1b <- lm(total_pr ~ n_bids, data = d_nona)glance(lm1b) %>%
select(adj.r.squared)
#> # A tibble: 1 x 1
#> adj.r.squared
#> <dbl>
#> 1 0.009727.3 lm1c
lm1c <- lm(total_pr ~ cond, data = d_nona)glance(lm1c) %>%
select(adj.r.squared)
#> # A tibble: 1 x 1
#> adj.r.squared
#> <dbl>
#> 1 0.009257.4 Moment mal…
Es muss einen besseren Weg geben, das ist auf die Dauer zu umständlich.
8 Automatisiertes Vorwärts-Regression
Zuerst legen wir fest, wie das maximal große Modell aussehen soll, bzw. welche Prädiktoren im maximal großen Modell enthalten sein sollen. Sagen wir b alle.
Dann sieht das Modell so aus.
lm_alle <- lm(total_pr ~ .,
data = d_nona) # kann etwas Zeit brauchenvorwaerts <- step(object = lm0,
direction = 'forward',
scope = formula(lm_alle),
trace = 0) # Infos zum Fortschritt ausdrucken?Dieses Vorgehen nennt man schrittweise (Vorwärts-)Regression.
Schauen wir uns das Ergebnis an:
tidy(vorwaerts)
#> # A tibble: 90 x 5
#> term estimate std.error statistic p.value
#> <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 (Intercept) 44.4 4.78 9.28 1.07e-12
#> 2 title10 Nintendo Wii Games - MarioKart… 71.8 5.99 12.0 1.05e-16
#> 3 titleBrand New Mario Kart Wii Comes wi… -6.55 4.39 -1.49 1.42e- 1
#> 4 titleBRAND NEW NINTENDO 1 WII MARIO KA… 6.22 5.61 1.11 2.72e- 1
#> 5 titleBRAND NEW NINTENDO MARIO KART WIT… -0.245 5.67 -0.0431 9.66e- 1
#> 6 titleBRAND NEW! FACTORY SEALED! MARIO … 0.397 6.13 0.0647 9.49e- 1
#> 7 titleMARIO KART - NINTENDO WII =======… 1.00 7.43 0.135 8.93e- 1
#> 8 titleMario Kart (Wii) with Wii Wheel -6.15 6.88 -0.894 3.76e- 1
#> 9 titleMario Kart & Wheel Nintendo W… -7.72 6.12 -1.26 2.12e- 1
#> 10 titleMARIO KART for Nintendo Wii -5.21 5.71 -0.913 3.65e- 1
#> # … with 80 more rowsUnd wie gut ist das \(R^2\)?
glance(vorwaerts)
#> # A tibble: 1 x 12
#> r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
#> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 0.993 0.981 3.59 82.2 1.80e-38 88 -313. 806. 1072.
#> # … with 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>Yeah!
9 Modellgüten der Modelle mit einem Prädiktor
Wir speichern und mal die Namen der Prädiktoren in einem Vektor; kann man vielleicht ja noch später gebrauchen …
predictor_names <-
d_nona %>%
select(-c(id, total_pr)) %>%
names()Voila:
predictor_names
#> [1] "duration" "n_bids" "cond" "start_pr" "ship_pr"
#> [6] "ship_sp" "seller_rate" "stock_photo" "wheels" "title"modellguete_1pred <-
d_nona %>%
select(-c(id, total_pr)) %>%
map_dfr( ~ lm(total_pr ~ .x, data = d_nona) %>% glance()) %>%
mutate(predictor = predictor_names) %>%
select(predictor, everything())
modellguete_1pred
#> # A tibble: 10 x 13
#> predictor r.squared adj.r.squared sigma statistic p.value df logLik AIC
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 duration 0.00170 -0.00543 25.8 0.238 6.26e- 1 1 -662. 1331.
#> 2 n_bids 0.0167 0.00972 25.7 2.38 1.25e- 1 1 -661. 1328.
#> 3 cond 0.0163 0.00925 25.7 2.32 1.30e- 1 1 -661. 1329.
#> 4 start_pr 0.00539 -0.00171 25.8 0.759 3.85e- 1 1 -662. 1330.
#> 5 ship_pr 0.294 0.289 21.7 58.4 3.03e-12 1 -638. 1281.
#> 6 ship_sp 0.0935 0.0461 25.2 1.97 6.31e- 2 7 -655. 1329.
#> 7 seller_r… 0.0000885 -0.00705 25.9 0.0124 9.12e- 1 1 -662. 1331.
#> 8 stock_ph… 0.00809 0.00100 25.8 1.14 2.87e- 1 1 -662. 1330.
#> 9 wheels 0.110 0.103 24.4 17.3 5.65e- 5 1 -654. 1314.
#> 10 title 0.987 0.970 4.43 59.5 1.15e-39 79 -354. 870.
#> # … with 4 more variables: BIC <dbl>, deviance <dbl>, df.residual <int>,
#> # nobs <int>Und dann stellen wir das grafisch dar:
modellguete_1pred %>%
ggplot(aes(x = reorder(predictor, -r.squared), y = r.squared)) +
geom_point(size = 5, color = "red", alpha = .7)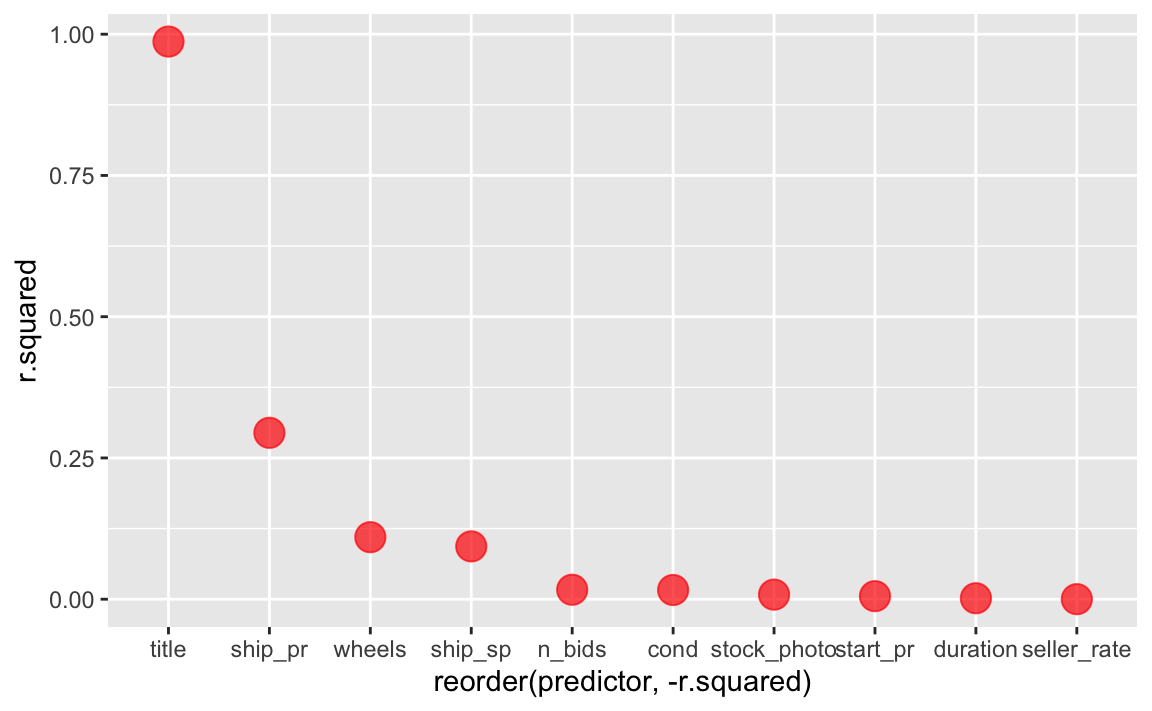
Welcher Prädiktor sollte also in einer Vorwärts-Regression als erstes aufgenommen werden (auf Basis dieser Ergebnisse)?
10 Reproduzierbarkeit
#> ─ Session info ───────────────────────────────────────────────────────────────────────────────────────────────────────
#> setting value
#> version R version 4.0.2 (2020-06-22)
#> os macOS Catalina 10.15.7
#> system x86_64, darwin17.0
#> ui X11
#> language (EN)
#> collate en_US.UTF-8
#> ctype en_US.UTF-8
#> tz Europe/Berlin
#> date 2020-12-10
#>
#> ─ Packages ───────────────────────────────────────────────────────────────────────────────────────────────────────────
#> package * version date lib source
#> assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.0.0)
#> backports 1.2.0 2020-11-02 [1] CRAN (R 4.0.2)
#> blogdown 0.21 2020-10-11 [1] CRAN (R 4.0.2)
#> bookdown 0.21 2020-10-13 [1] CRAN (R 4.0.2)
#> broom 0.7.2 2020-10-20 [1] CRAN (R 4.0.2)
#> callr 3.5.1 2020-10-13 [1] CRAN (R 4.0.2)
#> cellranger 1.1.0 2016-07-27 [1] CRAN (R 4.0.0)
#> cli 2.2.0 2020-11-20 [1] CRAN (R 4.0.2)
#> codetools 0.2-16 2018-12-24 [2] CRAN (R 4.0.2)
#> colorspace 2.0-0 2020-11-11 [1] CRAN (R 4.0.2)
#> crayon 1.3.4 2017-09-16 [1] CRAN (R 4.0.0)
#> DBI 1.1.0 2019-12-15 [1] CRAN (R 4.0.0)
#> dbplyr 2.0.0 2020-11-03 [1] CRAN (R 4.0.2)
#> desc 1.2.0 2018-05-01 [1] CRAN (R 4.0.0)
#> devtools 2.3.2 2020-09-18 [1] CRAN (R 4.0.2)
#> digest 0.6.27 2020-10-24 [1] CRAN (R 4.0.2)
#> dplyr * 1.0.2 2020-08-18 [1] CRAN (R 4.0.2)
#> ellipsis 0.3.1 2020-05-15 [1] CRAN (R 4.0.0)
#> evaluate 0.14 2019-05-28 [1] CRAN (R 4.0.0)
#> fansi 0.4.1 2020-01-08 [1] CRAN (R 4.0.0)
#> forcats * 0.5.0 2020-03-01 [1] CRAN (R 4.0.0)
#> fs 1.5.0 2020-07-31 [1] CRAN (R 4.0.2)
#> generics 0.1.0 2020-10-31 [1] CRAN (R 4.0.2)
#> ggplot2 * 3.3.2 2020-06-19 [1] CRAN (R 4.0.0)
#> glue 1.4.2 2020-08-27 [1] CRAN (R 4.0.2)
#> gtable 0.3.0 2019-03-25 [1] CRAN (R 4.0.0)
#> haven 2.3.1 2020-06-01 [1] CRAN (R 4.0.0)
#> hms 0.5.3 2020-01-08 [1] CRAN (R 4.0.0)
#> htmltools 0.5.0 2020-06-16 [1] CRAN (R 4.0.0)
#> httr 1.4.2 2020-07-20 [1] CRAN (R 4.0.2)
#> jsonlite 1.7.1 2020-09-07 [1] CRAN (R 4.0.2)
#> knitr 1.30 2020-09-22 [1] CRAN (R 4.0.2)
#> lifecycle 0.2.0 2020-03-06 [1] CRAN (R 4.0.0)
#> lubridate 1.7.9.2 2020-11-13 [1] CRAN (R 4.0.2)
#> magrittr 2.0.1 2020-11-17 [1] CRAN (R 4.0.2)
#> memoise 1.1.0 2017-04-21 [1] CRAN (R 4.0.0)
#> modelr 0.1.8 2020-05-19 [1] CRAN (R 4.0.0)
#> munsell 0.5.0 2018-06-12 [1] CRAN (R 4.0.0)
#> pillar 1.4.7 2020-11-20 [1] CRAN (R 4.0.2)
#> pkgbuild 1.1.0 2020-07-13 [1] CRAN (R 4.0.2)
#> pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.0.0)
#> pkgload 1.1.0 2020-05-29 [1] CRAN (R 4.0.0)
#> prettyunits 1.1.1 2020-01-24 [1] CRAN (R 4.0.0)
#> processx 3.4.5 2020-11-30 [1] CRAN (R 4.0.2)
#> ps 1.4.0 2020-10-07 [1] CRAN (R 4.0.2)
#> purrr * 0.3.4 2020-04-17 [1] CRAN (R 4.0.0)
#> R6 2.5.0 2020-10-28 [1] CRAN (R 4.0.2)
#> Rcpp 1.0.5 2020-07-06 [1] CRAN (R 4.0.2)
#> readr * 1.4.0 2020-10-05 [1] CRAN (R 4.0.2)
#> readxl 1.3.1 2019-03-13 [1] CRAN (R 4.0.0)
#> remotes 2.2.0 2020-07-21 [1] CRAN (R 4.0.2)
#> reprex 0.3.0 2019-05-16 [1] CRAN (R 4.0.0)
#> rlang 0.4.9 2020-11-26 [1] CRAN (R 4.0.2)
#> rmarkdown 2.5 2020-10-21 [1] CRAN (R 4.0.2)
#> rprojroot 2.0.2 2020-11-15 [1] CRAN (R 4.0.2)
#> rstudioapi 0.13.0-9000 2020-12-09 [1] Github (rstudio/rstudioapi@4baeb39)
#> rvest 0.3.6 2020-07-25 [1] CRAN (R 4.0.2)
#> scales 1.1.1 2020-05-11 [1] CRAN (R 4.0.0)
#> sessioninfo 1.1.1 2018-11-05 [1] CRAN (R 4.0.0)
#> stringi 1.5.3 2020-09-09 [1] CRAN (R 4.0.2)
#> stringr * 1.4.0 2019-02-10 [1] CRAN (R 4.0.0)
#> testthat 3.0.0 2020-10-31 [1] CRAN (R 4.0.2)
#> tibble * 3.0.4 2020-10-12 [1] CRAN (R 4.0.2)
#> tidyr * 1.1.2 2020-08-27 [1] CRAN (R 4.0.2)
#> tidyselect 1.1.0 2020-05-11 [1] CRAN (R 4.0.0)
#> tidyverse * 1.3.0 2019-11-21 [1] CRAN (R 4.0.0)
#> usethis 1.6.3 2020-09-17 [1] CRAN (R 4.0.2)
#> vctrs 0.3.5 2020-11-17 [1] CRAN (R 4.0.2)
#> withr 2.3.0 2020-09-22 [1] CRAN (R 4.0.2)
#> xfun 0.19 2020-10-30 [1] CRAN (R 4.0.2)
#> xml2 1.3.2 2020-04-23 [1] CRAN (R 4.0.0)
#> yaml 2.2.1 2020-02-01 [1] CRAN (R 4.0.0)
#>
#> [1] /Users/sebastiansaueruser/Rlibs
#> [2] /Library/Frameworks/R.framework/Versions/4.0/Resources/library