- 0.1 Überblick
- 1 Stärkster univariater Prädiktor der Dozentenbeurteilung
- 2 für univariate Regression von
scoreauf den stärksten Prädiktor - 3 Visualisieren Sie die univariate Regression
- 4 Vergleich zur Korrelation
- 5 Standardisierte Prädiktoren
- 6 Lebenserwartung nach Kontinent berechnen
- 7 Lebenserwartung nach Kontinent visualisieren
- 8 Lebenserwartung nach Kontinent und Regression
- 9 Berechnung der Lebenswertung für einen spezifischen Kontinent
- 10 Bedeutung der Residuen in der Regressionsanalyse
- 11 Konfundierung
- 12 Optimierungskriterium der Regression
0.1 Überblick
Diese Aufgaben beziehen sich auf Kapitel 5 aus dem Buch ModernDive.
library(tidyverse) # Datenjudo
library(moderndive) # Daten
library(gapminder) # DatenAls Datensätze werden verwendet evals und gapminder:
data("evals")
data("gapminder")1 Stärkster univariater Prädiktor der Dozentenbeurteilung
1.1 Aufgabe
Identifizieren Sie den stärksten (univariaten) Prädiktor für die (Höhe der) Dozentenbeurteilung! (Datensatz evals aus dem Paket modernDive)
1.2 Hilfe
Hilfe zur Tabelle evals bekommt man so:
help(evals)1.3 Hinweise
Ein möglicher Start ist: Berechnen Sie die Korrelationen der möglichen Prädiktoren (UV) mit dem Kriterium score (AV, Zielvariable)!
Unsere Forschungsfrage lautet also:
Welche Variablenausprägungen gehen mit einer guten Dozentenbeurteilung einher?
Anstelle von “gehen einher” könnte man sagen “sind korreliert mit” oder “sind assoziiert mit” oder “sind statistisch abhängig voneinander”. Geht man von einer Kausalbeziehung aus, könnte man sagen “welche Variable hat den größten Einfluss auf die Dozentenbeurteilung?”. Allerdings braucht man für die vollmundinge Behauptung einer Kausalbeziehung schon gute Argumente.
Wir suchen also die “wichtigste” UV!
Mit “univariat” ist gemeint, dass wir nur Modelle in Betracht ziehen, in denen es eine UV gibt.
Schauen wir uns die ersten paar Zeilen auf evals an:
head(evals)## # A tibble: 6 x 14
## ID prof_ID score age bty_avg gender ethnicity language rank pic_outfit
## <int> <int> <dbl> <int> <dbl> <fct> <fct> <fct> <fct> <fct>
## 1 1 1 4.7 36 5 female minority english tenu… not formal
## 2 2 1 4.1 36 5 female minority english tenu… not formal
## 3 3 1 3.9 36 5 female minority english tenu… not formal
## 4 4 1 4.8 36 5 female minority english tenu… not formal
## 5 5 2 4.6 59 3 male not mino… english tenu… not formal
## 6 6 2 4.3 59 3 male not mino… english tenu… not formal
## # … with 4 more variables: pic_color <fct>, cls_did_eval <int>,
## # cls_students <int>, cls_level <fct>Um herauszufinden, welche Variable mit der AV score positiv einhergeht, kann man sich ein Streudiagramm ausgeben und zwar für jeden (numerischen) Prädiktor:
evals %>%
ggplot() +
aes(x = cls_students, y = score) +
geom_point()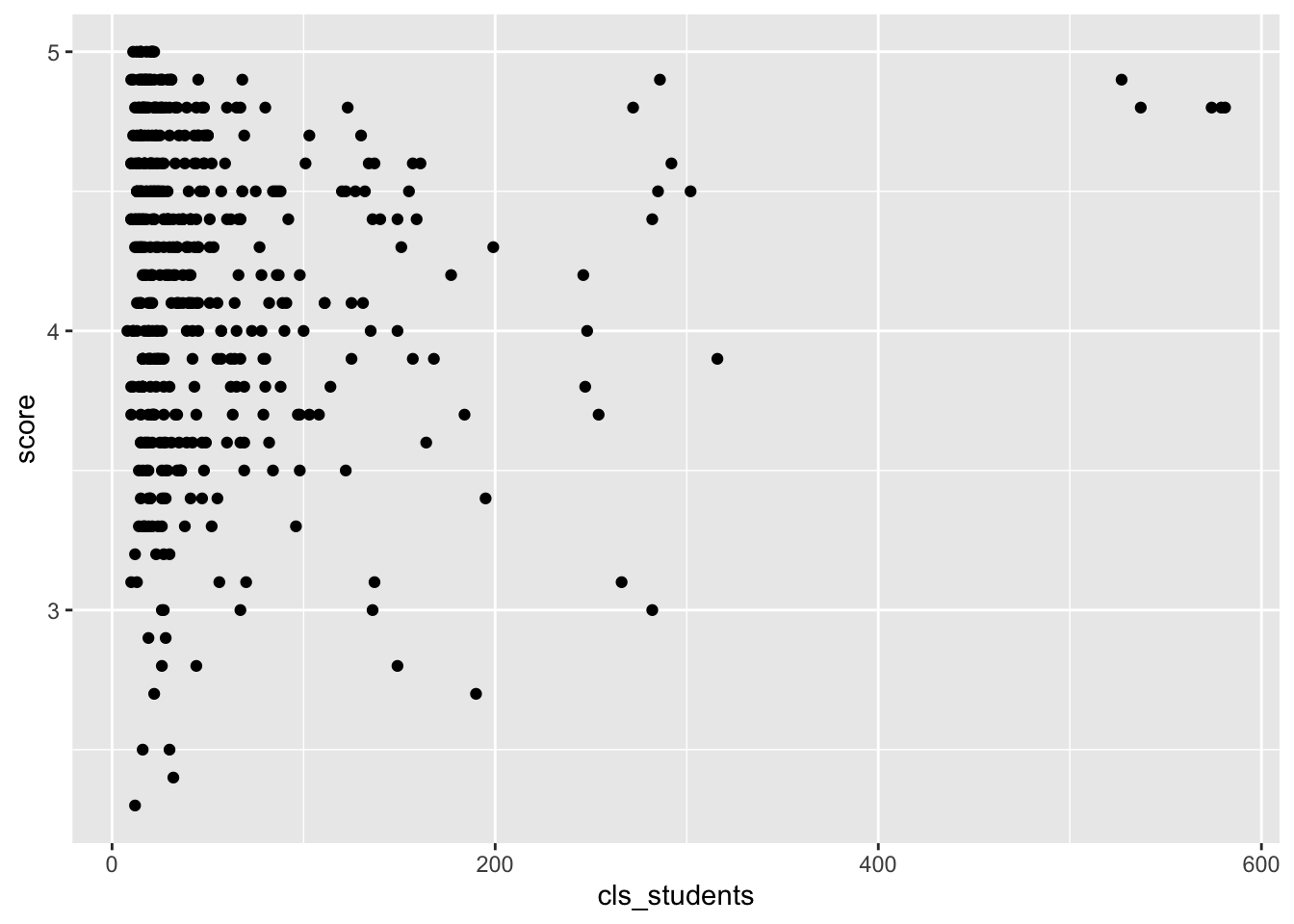
evals %>%
ggplot() +
aes(x = bty_avg, y = score) +
geom_point()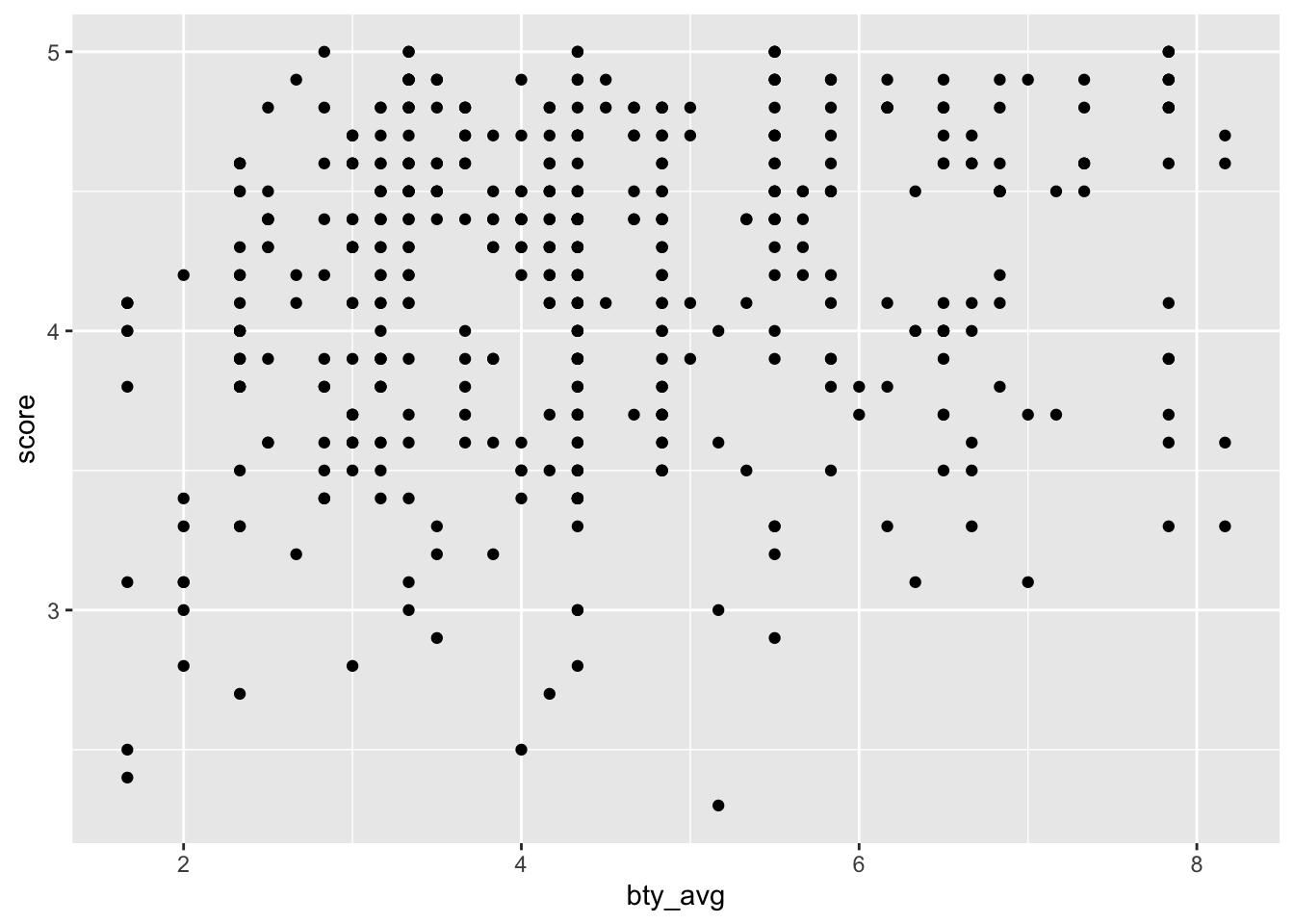
Hm, die Schönheit einer Lehrkraft könnte eine (kleine) Rolle spielen.
1.4 Lösung
Man kann die Korrelation jedes (numerischen) Prädiktors berechnen und dann die höchste Korrelation ablesen:
evals %>%
summarise(r_bty = cor(score, bty_avg),
r_ge = cor(score, age))## # A tibble: 1 x 2
## r_bty r_ge
## <dbl> <dbl>
## 1 0.187 -0.107Und so weiter.
Aber was machen wir mit den nicht-numerischen Werten? Die kann man nicht (direkt) korrelieren. Lassen wir die mal außen vor.
1.5 Für Fortgeschrittene
So geht es komfortabler:
library(corrr)
evals %>%
select(where(is.numeric)) %>% # nimm die Spalten, wo eine numerische Spalte ist
select(-c(ID, prof_ID)) %>% # Prof_ID und ID brauchen wir nicht
correlate() %>% # korrelieren
focus(score) %>% # Fokus auf `score`
arrange() # sortieren##
## Correlation method: 'pearson'
## Missing treated using: 'pairwise.complete.obs'## # A tibble: 4 x 2
## term score
## <chr> <dbl>
## 1 age -0.107
## 2 bty_avg 0.187
## 3 cls_did_eval 0.0628
## 4 cls_students 0.02602 für univariate Regression von score auf den stärksten Prädiktor
2.1 Aufgabe
Führen Sie eine einfache (univariate) Regression von score (AV) zurück auf den stärksten Prädiktor. Wenn Sie den stärksten Prädiktor nicht gefunden haben, wählen Sie einen beliebigen Prädiktor. Geben Sie das an.
2.2 Lösung
lm1 <- lm(score ~ bty_avg, data = evals)
summary(lm1)##
## Call:
## lm(formula = score ~ bty_avg, data = evals)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.9246 -0.3690 0.1420 0.3977 0.9309
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.88034 0.07614 50.96 < 2e-16 ***
## bty_avg 0.06664 0.01629 4.09 5.08e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5348 on 461 degrees of freedom
## Multiple R-squared: 0.03502, Adjusted R-squared: 0.03293
## F-statistic: 16.73 on 1 and 461 DF, p-value: 5.083e-05Das liegt bei etwa 3%.
3 Visualisieren Sie die univariate Regression
3.1 Aufgabe
Visualisieren Sie die Regression aus der letzter Aufgabe anhand eines geeigneten Diagramms. Begründen Sie Ihre Wahl. Wenn Sie die letzte Aufgabe nicht gelöst haben, wählen Sie eine beliebige Regression.
3.2 Lösung
evals %>%
ggplot(aes(x = bty_avg, y = score)) +
geom_point() +
geom_smooth(method = "lm")## `geom_smooth()` using formula 'y ~ x'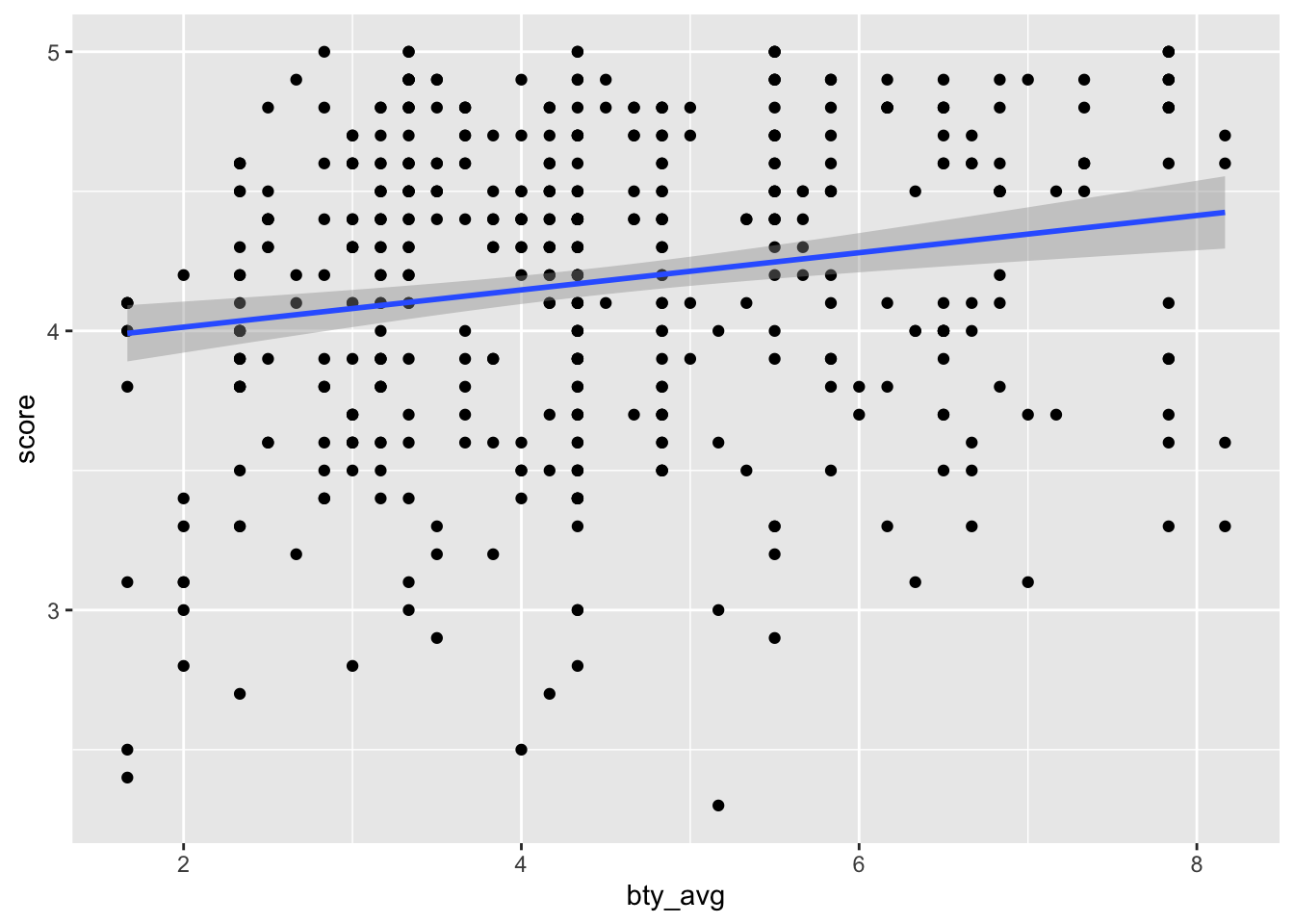
3.3 Variante
evals %>%
ggplot(aes(x = bty_avg, y = score)) +
geom_density_2d() + # geom_hex()
geom_smooth(method = "lm")## `geom_smooth()` using formula 'y ~ x'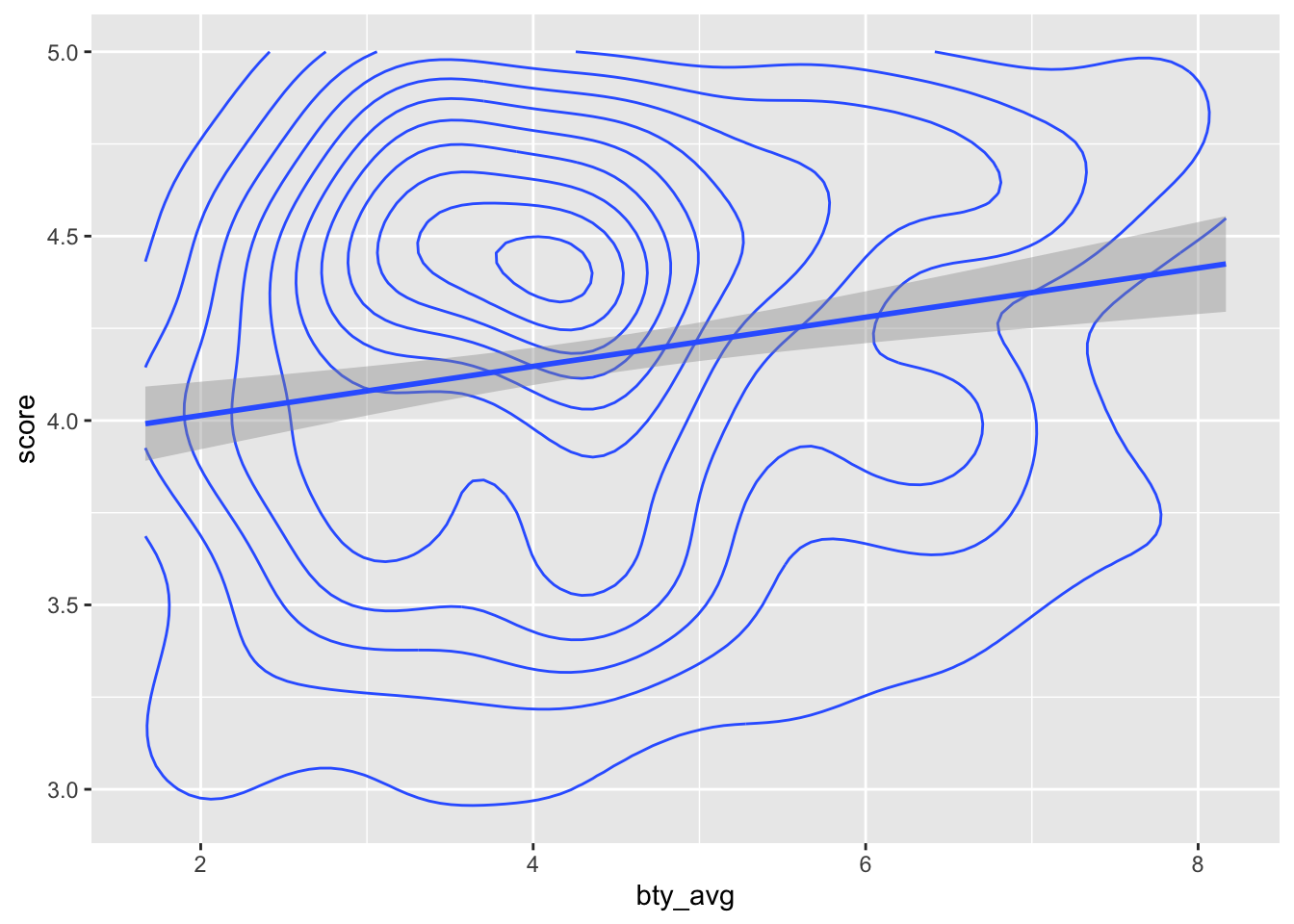
4 Vergleich zur Korrelation
4.1 Aufgabe
Was ist der Unterschied zwischen den folgenden drei Kennwerten:
Hinweis: Beziehen Sie sich auf den Kontext der Regressionsanalyse (lineare Modelle).
4.2 Lösung
- gibt die Höhe des durch das Regressionsmodell erklärten Varianzanteils an.
- gibt die Steigung der Regressionsgeraden an, gibt den Wert des Achsenabschnitts an.
- gibt die Höhe des Korrelationskoeffizienten wieder. Bei univariaten Regressionsmodellen ist das Quadrat von .
5 Standardisierte Prädiktoren
5.1 Aufgabe
Führen Sie eine z-Standardisierung des Prädiktors (UV) und des Kriteriums (AV) durch. Mit diesen transformierten Variablen wiederholen Sie dann die Regression. Diskutieren Sie die Veränderung.
5.2 Lösung
evals %>%
mutate(bty_avg_z = ((bty_avg - mean(bty_avg)) / sd(bty_avg)),
score_z = ((score - mean(score)) / sd(score))) -> evalslm2 <- lm(score_z ~ bty_avg_z, data = evals)
summary(lm2)##
## Call:
## lm(formula = score_z ~ bty_avg_z, data = evals)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.5388 -0.6785 0.2611 0.7312 1.7116
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.371e-16 4.570e-02 0.00 1
## bty_avg_z 1.871e-01 4.575e-02 4.09 5.08e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9834 on 461 degrees of freedom
## Multiple R-squared: 0.03502, Adjusted R-squared: 0.03293
## F-statistic: 16.73 on 1 and 461 DF, p-value: 5.083e-05Die Werte von und haben sich geändert. ist gleich geblieben.
Das Diagramm sieht fast genau aus:
evals %>%
ggplot(aes(x = bty_avg_z, y = score_z)) +
geom_point() +
geom_smooth(method = "lm")## `geom_smooth()` using formula 'y ~ x'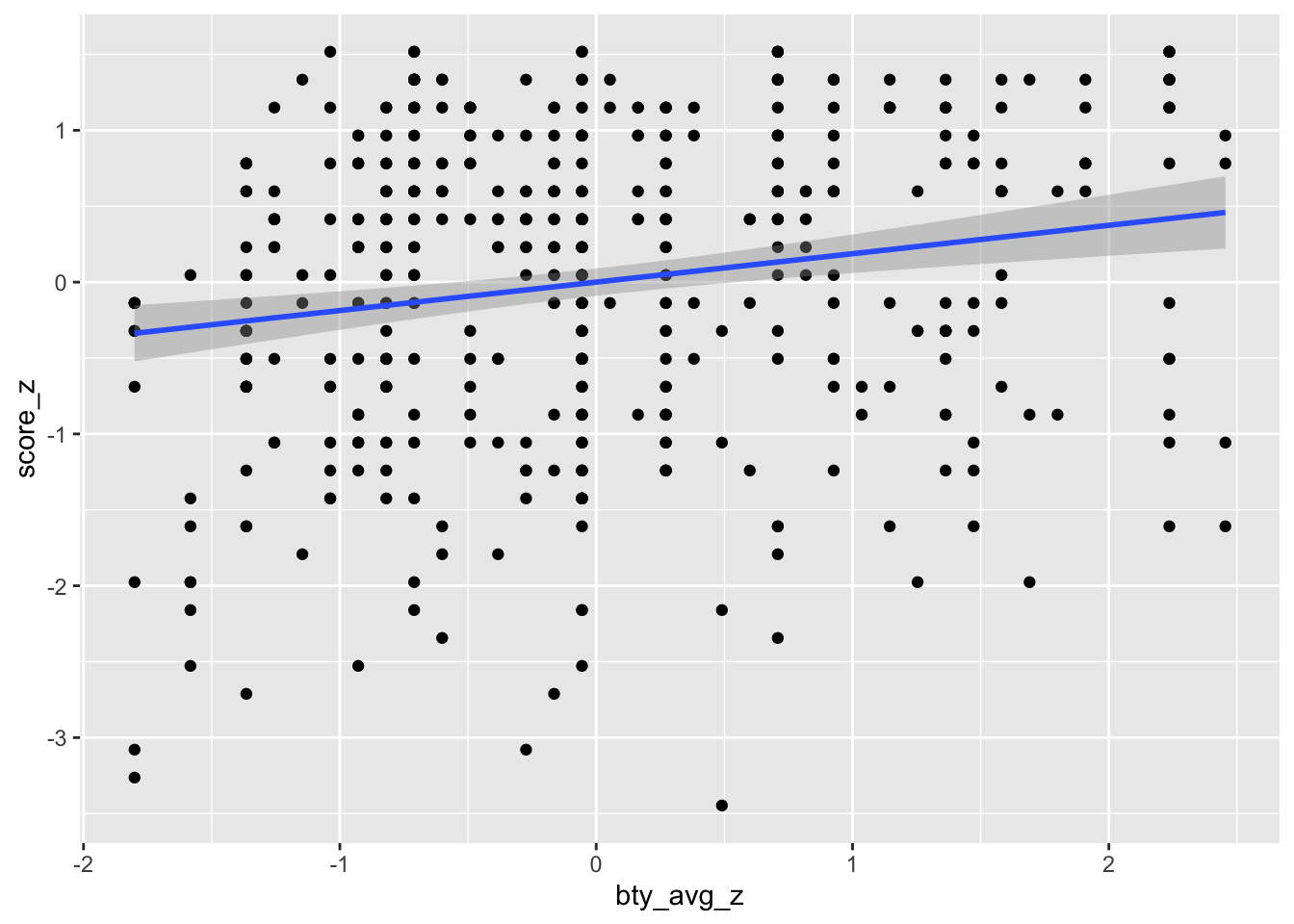
6 Lebenserwartung nach Kontinent berechnen
6.1 Aufgabe
Fassen Sie die mittlere Lebenserwartungen nach Kontinent zusammen.
6.2 Lösung
Daten laden:
data("gapminder")gapminder %>%
group_by(continent) %>%
summarise(lifeExp = mean(lifeExp))## # A tibble: 5 x 2
## continent lifeExp
## * <fct> <dbl>
## 1 Africa 48.9
## 2 Americas 64.7
## 3 Asia 60.1
## 4 Europe 71.9
## 5 Oceania 74.36.3 Hinweis
Sinnvoller wäre es, vorher nach einem Jahr zu filtern, entsprechend dem Vorgehen im Buch.
gapminder %>%
filter(year == 2007) -> gapminder_2007gapminder_2007 %>%
group_by(continent) %>%
summarise(lifeExp = mean(lifeExp))## # A tibble: 5 x 2
## continent lifeExp
## * <fct> <dbl>
## 1 Africa 54.8
## 2 Americas 73.6
## 3 Asia 70.7
## 4 Europe 77.6
## 5 Oceania 80.7Speichern wir die zusammengefassten Statistiken für etwaige spätere Verwendung:
gapminder_2007 %>%
group_by(continent) %>%
summarise(lifeExp_avg = mean(lifeExp, na.rm = TRUE),
lifeExp_sd = sd(lifeExp, na.rm = TRUE)) -> gapminder_2007_summary7 Lebenserwartung nach Kontinent visualisieren
7.1 Aufgabe
Visualisieren Sie die Lebenserwartung nach Kontinent mit einem geeigneten Diagramm. Begründen Sie Ihre Wahl.
7.2 Lösung
gapminder %>%
filter(year == 2007) %>%
ggplot() +
aes(x = continent, y = lifeExp) +
geom_boxplot()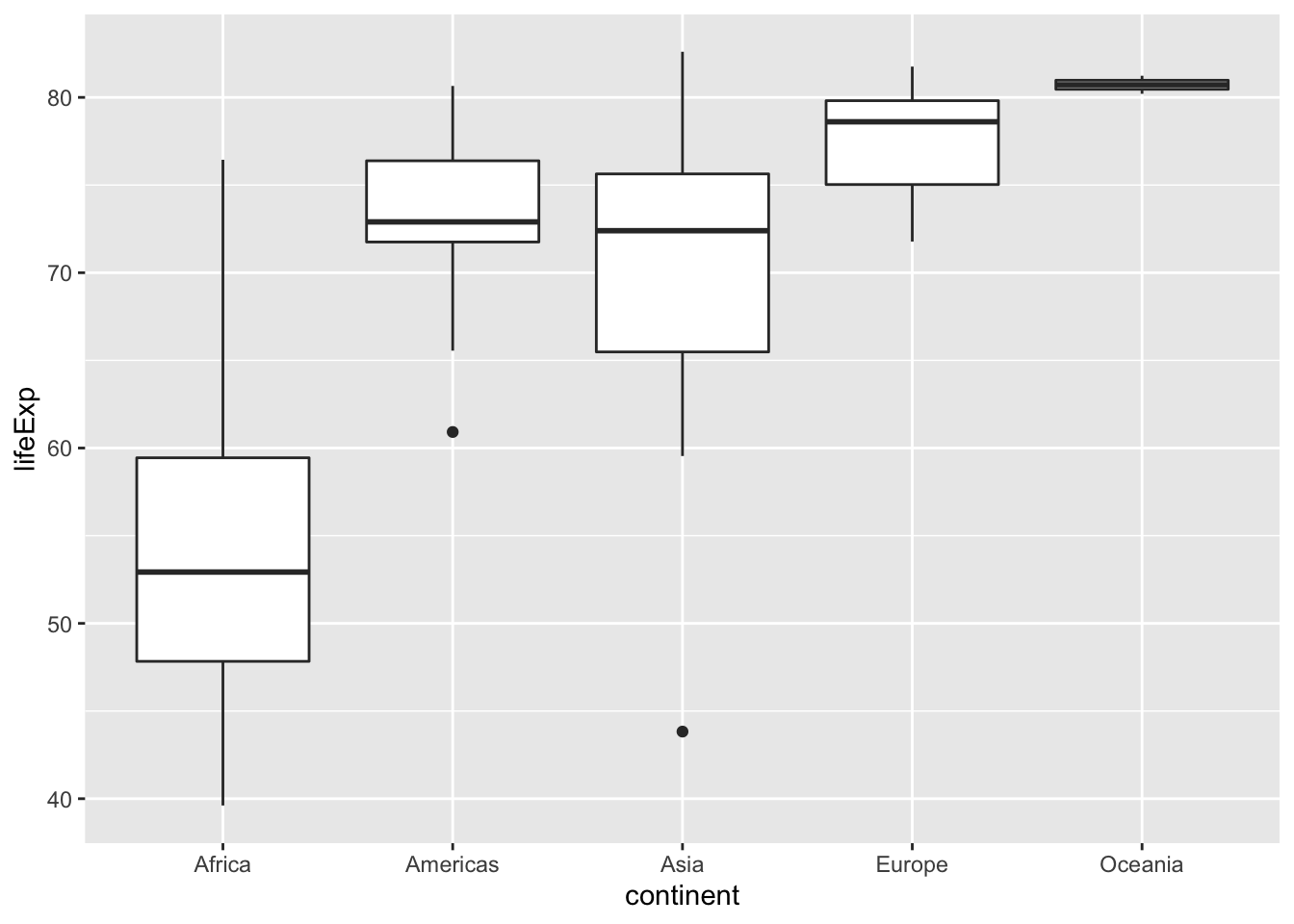
Da die Boxplots aber Mediane anstelle von Mittelwerten zeigen, wäre folgendes Vorgehen sinvoller:
gapminder_2007_summary %>%
ggplot() +
aes(x = continent, y = lifeExp_avg) +
geom_point() +
geom_errorbar(aes(ymin = lifeExp_avg - lifeExp_avg + 2*lifeExp_sd,
ymax = lifeExp_avg + lifeExp_avg + 2*lifeExp_sd))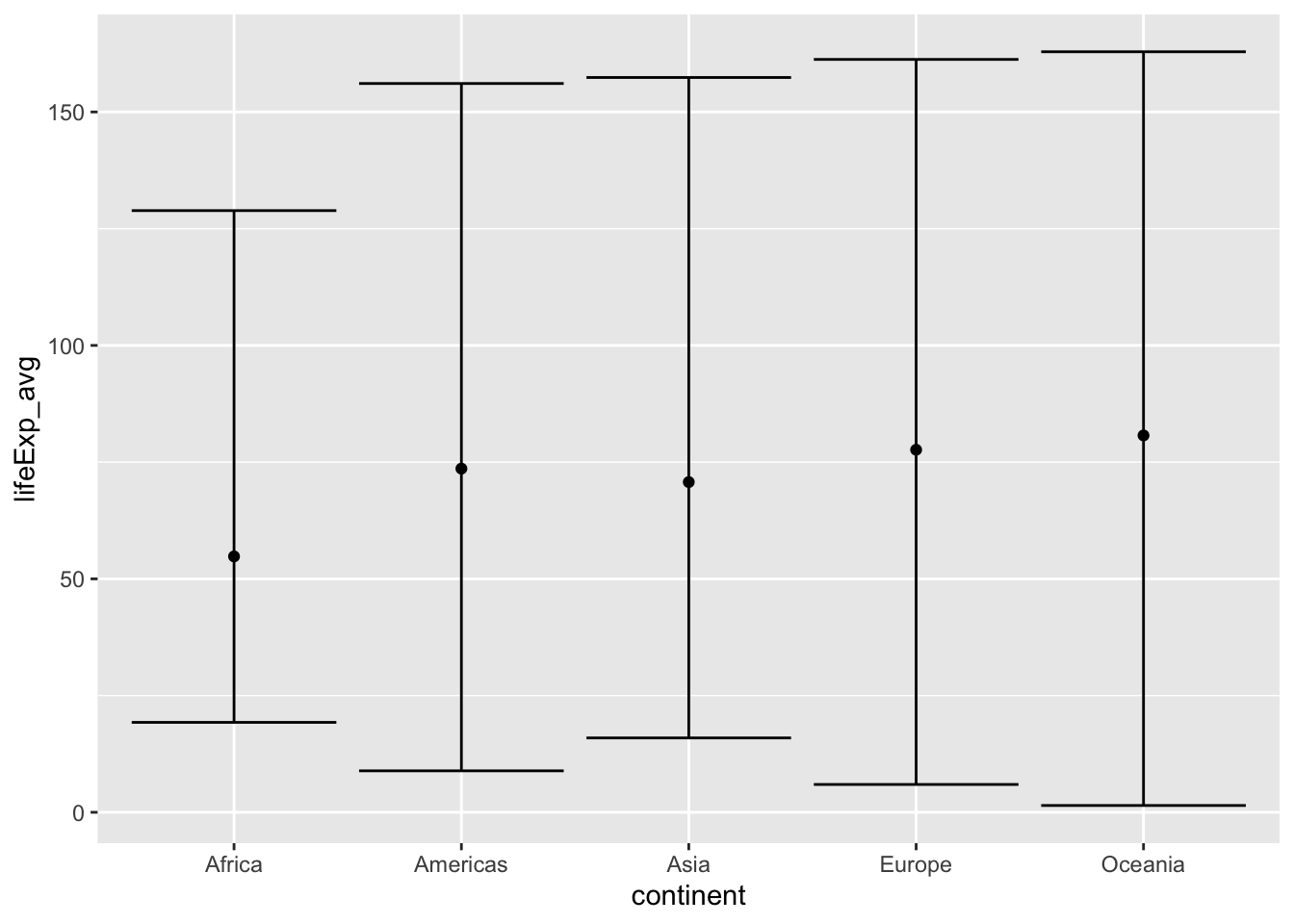
Oder so:
gapminder %>%
filter(year == 2007) %>%
ggplot() +
aes(x = continent, y = lifeExp) +
geom_boxplot() +
geom_point(data = gapminder_2007_summary,
aes(y = lifeExp_avg),
color = "red",
size = 5,
alpha = .7) 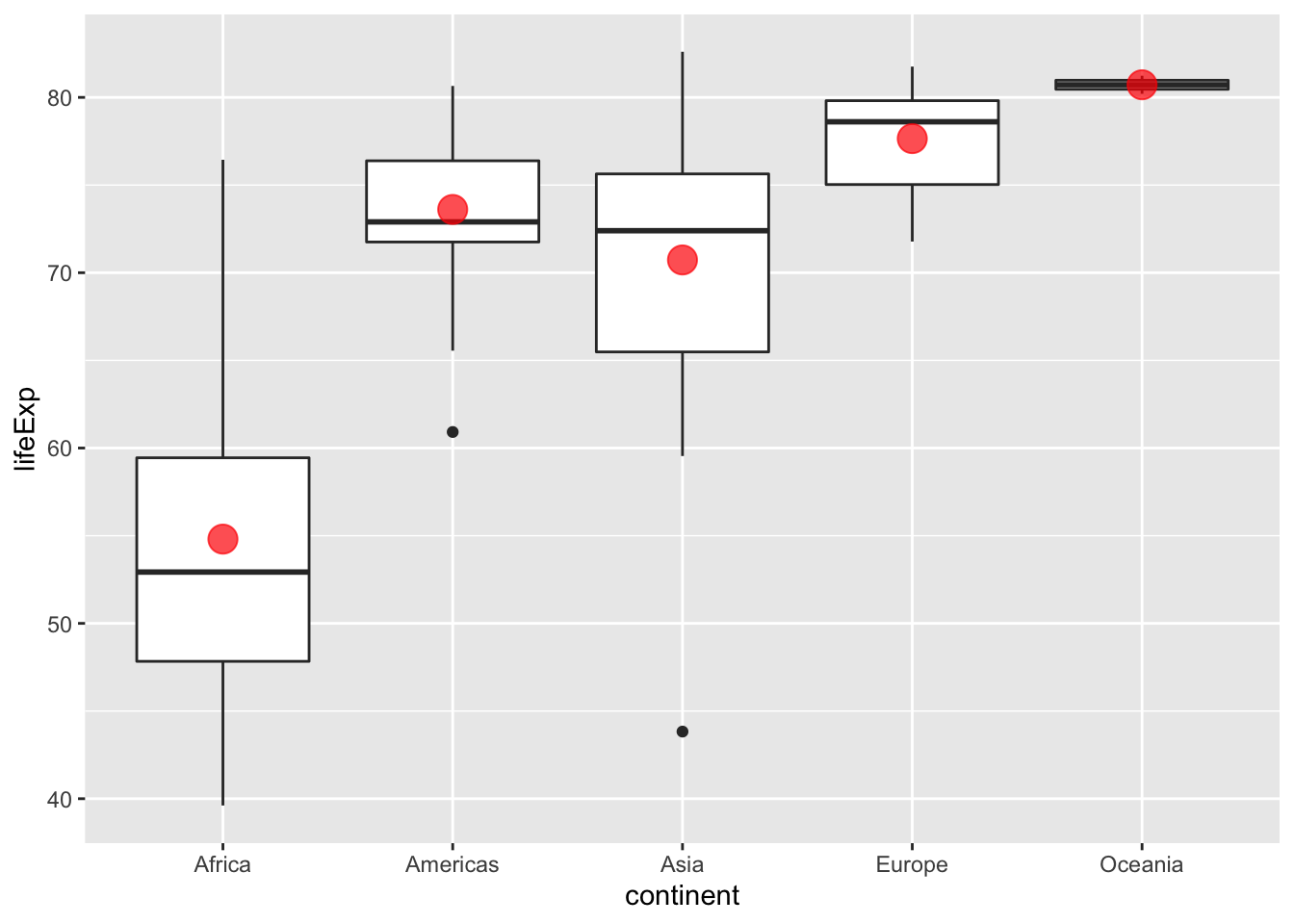
8 Lebenserwartung nach Kontinent und Regression
8.1 Aufgabe
Führen Sie eine Regression mit Lebenserwartung als AV und Kontinent als UV durch. Vergleichen Sie die Regressionskoeffizienten mit den Mittelwerten aus den vorherigen Aufgaben. Was fällt Ihnen auf? (Wenn Sie die Mittelwerte nicht berechnet haben, schlagen Sie sie im Buch nach.)
8.2 Lösung
lm3 <- lm(lifeExp ~ continent, data = gapminder_2007)
summary(lm3)##
## Call:
## lm(formula = lifeExp ~ continent, data = gapminder_2007)
##
## Residuals:
## Min 1Q Median 3Q Max
## -26.9005 -4.0399 0.2565 3.3840 21.6360
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 54.806 1.025 53.446 < 2e-16 ***
## continentAmericas 18.802 1.800 10.448 < 2e-16 ***
## continentAsia 15.922 1.646 9.675 < 2e-16 ***
## continentEurope 22.843 1.695 13.474 < 2e-16 ***
## continentOceania 25.913 5.328 4.863 3.12e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.395 on 137 degrees of freedom
## Multiple R-squared: 0.6355, Adjusted R-squared: 0.6249
## F-statistic: 59.71 on 4 and 137 DF, p-value: < 2.2e-16Die Estimate-Werte entsprechen genau den Mittelwerten pro Kontinenten bzw. den Unterschieden der Kontinente im Vergleich zum “Referenzkontinent”, Afrika.
9 Berechnung der Lebenswertung für einen spezifischen Kontinent
9.1 Aufgabe
Nutzen Sie die Ausgabe der Regressionsanalyse (lm()), um die Rechenvorschrift der Lebenserwartung für
- Afrika
- Europa
aufzuschreiben.
9.2 Lösung
lifeExp_Africa = 54.806
lifeExp_Europe = 65.806 + 22.843
10 Bedeutung der Residuen in der Regressionsanalyse
10.1 Aufgabe
Erläutern Sie:
- Was gibt diese Formel wieder:
- Welchen Effekt hat es, wenn man die Formel wie folgt verändert: ?
- Wie nennt man die Größe ?
10.2 Lösung
- Der Ausdruck gibt die Summe der Residuen wieder. (Diese summieren sich zu Null auf.)
- Damit werden die Quadrate der Residuen aufaddiert; das Vorzeichen verliert dabei die Bedeutung.
- Der Ausdruck definiert das Residuum, .
11 Konfundierung
11.1 Aufgabe
Geben Sie ein Beispiel für eine Konfundierung (confounding) aus Ihrem persönlichen Umfeld!
11.2 Lösung
Freude am Unterricht (F) und Klausurerfolg (E) seien korreliert. In Wahrheit sei Lernzeit (L) die konfundierende Variable.
12 Optimierungskriterium der Regression
12.1 Aufgabe
Die Regression “sucht” nach der am besten passenden Geraden (best fitting line).
- Welcher Ausdruck wird dabei minimiert?
- Warum wird er minimiert (und nicht maximiert)?
- Lassen Sie sich diesen Term in R ausgeben für Ihre Regression zur Lebenserwartung nach Kontinent.
12.2 Lösung
- Die Summe der quadrierten Residuen wird minimiert (s.o.).
- Es wir die Lösung gesucht, bei der die Residuen minimal sind; die Vorhersage also maximal gut.
get_regression_points(lm3) %>%
select(residual)## # A tibble: 142 x 1
## residual
## <dbl>
## 1 -26.9
## 2 -1.23
## 3 17.5
## 4 -12.1
## 5 1.71
## 6 0.516
## 7 2.18
## 8 4.91
## 9 -6.67
## 10 1.79
## # … with 132 more rows12.3 Hinweis
Die Summe der Residuen beträgt:
get_regression_points(lm3) %>%
select(residual) %>%
summarise(residual_sum = sum(residual))## # A tibble: 1 x 1
## residual_sum
## <dbl>
## 1 0.009Das ist praktisch Null.
Die Summe der quadrierten Residuen beträgt:
get_regression_points(lm3) %>%
select(residual) %>%
summarise(residual_sum = sum(residual^2)) -> residual_squared_sum
residual_squared_sum## # A tibble: 1 x 1
## residual_sum
## <dbl>
## 1 7491.Die Summe der quadrierten Abweichungen vom Mittelwert beträgt:
get_regression_points(lm3) %>%
mutate(dev_mean_sq = (lifeExp - mean(lifeExp))^2) %>%
summarise(dev_mean_sq_sum = sum(dev_mean_sq)) -> dev_mean_squared_sum
dev_mean_squared_sum## # A tibble: 1 x 1
## dev_mean_sq_sum
## <dbl>
## 1 20552.Teilt man residual_squared_sum durch dev_mean_squared_sum, so erhält man den nicht erklärten Streuungsanteil:
variance_unexplained <- residual_squared_sum / dev_mean_squared_sum
variance_unexplained## residual_sum
## 1 0.3645013Zieht man von 1 den Anteil nicht erklärter Varianz ab, so erhält man :
1 - variance_unexplained## residual_sum
## 1 0.6354987Vergleiche:
summary(lm3)##
## Call:
## lm(formula = lifeExp ~ continent, data = gapminder_2007)
##
## Residuals:
## Min 1Q Median 3Q Max
## -26.9005 -4.0399 0.2565 3.3840 21.6360
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 54.806 1.025 53.446 < 2e-16 ***
## continentAmericas 18.802 1.800 10.448 < 2e-16 ***
## continentAsia 15.922 1.646 9.675 < 2e-16 ***
## continentEurope 22.843 1.695 13.474 < 2e-16 ***
## continentOceania 25.913 5.328 4.863 3.12e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.395 on 137 degrees of freedom
## Multiple R-squared: 0.6355, Adjusted R-squared: 0.6249
## F-statistic: 59.71 on 4 and 137 DF, p-value: < 2.2e-16