Load packages

library(tidyverse)
library(MASS)

Motivation

It is well-known that the notorious (Pearson’s) correlation cannot exceed an absolute value greater than 1, that is

$$-1\le r\le +1$$

or

$$|r|\le 1$$

However, proofing this fact is less straightforward. A classical way of proofing the above inequality is by using the Cauchy-Schwarz inequality. From a teacher’s perspective, the CS inequality may not be ideal, because the students may lack some knowledge necessary for appreciating this proof. In order to provide teachers’s (or anyone else for that matter), this posts provides an alternative way, one that does not demand much more than basic algebra and some knowledge about descriptive statistics (particularly including z-scores and correlation). This posts builds on this paper.

Definitions

Assume there are two sets of measurements (values), where $x_i$ and $y_i$ denote the $i$ measurement, $i=1,2,\dots ,n$. The (empirical) correlation $r$ can then be defined as

$$r_{xy}=r=\frac{s_{xy}}{s_x{s}_y}$$

where $s_x$ denotes the standard deviation of $X$, and $s_{x}y$ the covariancee of $x$ and $y$.

Let’s denote $x_i-\overline{x}$ with $d{x}_i$ (and $d{y}_i$ in the obvious way).

Note the analoguous definition of $s_x^2$ and $s_{xy}$:

$$\begin{array}{cc}{s}_x^2& =\frac{1}{n}\sum d{x}_i^2=\frac{1}{n}\sum (d{x}_i\cdot d{x}_i)\\ s_{xy}& =\frac{1}{n}\sum (d{x}_i\cdot d{y}_i)\end{array}$$

Hence

$$\begin{array}{c}\sqrt{s_x^2\cdot s_y^2}=s_{xy}\end{array}$$

In other words: The variance $s_x=\frac{1}{n}\sum (d{x}_i\cdot d{x}_i)$ equals the covariance if we let the second $d{x}_i$ equal $d{y}_i$.

$$\begin{array}{cc}{s}_x{s}_y& =\sqrt{\frac{1}{n}\sum (d{x}_i{)}^2\cdot \frac{1}{n}\sum (d{y}_i{)}^2}\\ & =\frac{1}{n}\sum (d{x}_i\cdot d{y}_i)\end{array}$$

As the z-score is defined as

$$z=\frac{x_i-\overline{x}}{s_x}$$

we may also define $r$ as

$$r=\frac{1}{n}\sum (z_x\cdot z_y)$$

Intuition about the magnitude or $r$

Let’s simulate some correlated data.

d <- mvrnorm(n = 100, mu = c(0,0) , Sigma = matrix(c(1, 0.7, 0.7, 1), nrow = 2), empirical = TRUE) 

d <- as_tibble(d)

Let’s color the dots with respect of the sign of the product of $V1$ and $V2$.

d <- d %>% 
  mutate(dot_sign = ifelse(V1*V2 > 0, "pos", "neg"))

ggplot(d, aes(V1, V2, color = dot_sign)) +
  geom_point() +
  geom_vline(xintercept = mean(d$V1), linetype = "dashed") +
  geom_hline(yintercept = mean(d$V1), linetype = "dashed")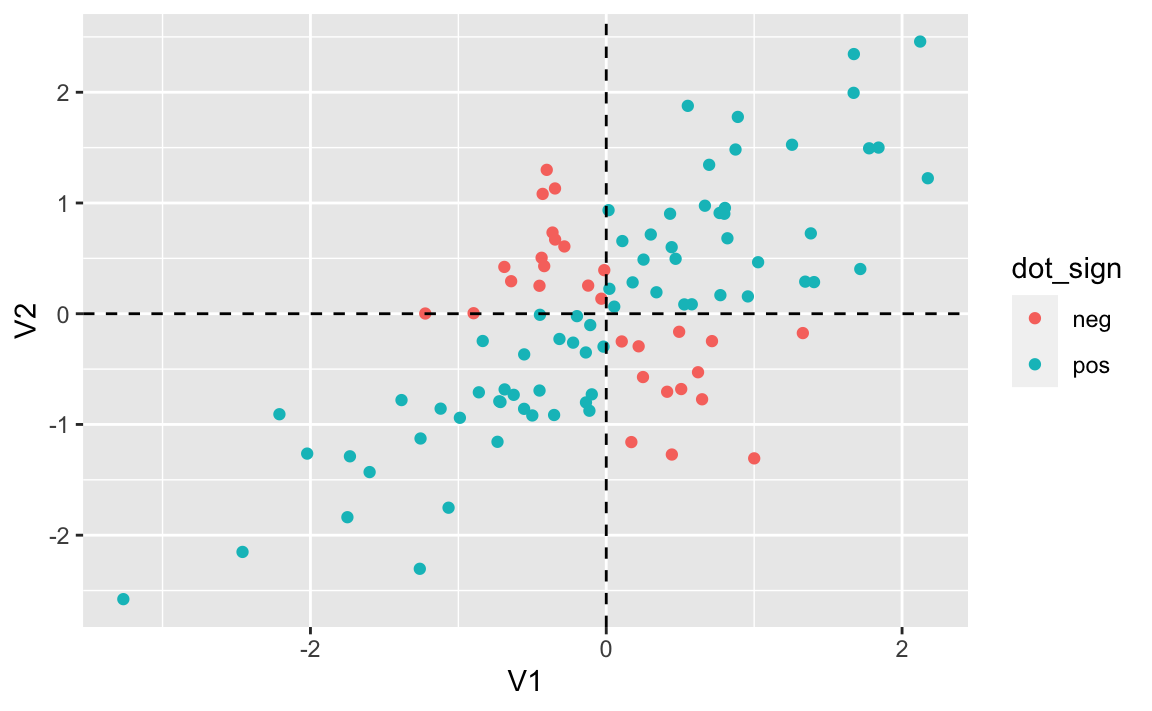

We see four “regions”, two with positive and two with negative sign.

Observe that in the two “positive” regions the product of V1 and V2 is positive, and in the two negative regions, their product is negative.

Some properties of z-scores and their sums and products

Further note that - as squares cannot be negative - this term must be nonnegative:

$$(z_{x_i}+z_{y_i}{)}^2$$

for each $i$.

Similarly,

$$\frac{1}{n}\sum (z_{x_i}+z_{y_i}{)}^2\ge 0\text{eq. 3}$$

Read the above equation as “the average squared sum of two z-scores must be nonnegative.”

Now multiply out the binomial part of the last step:

$$\begin{array}{cc}\frac{1}{n}\sum [z_x^2+2z_x{z}_y+z_y^2]& \ge 0\\ \frac{1}{n}\sum z_x^2+2\frac{1}{n}\sum z_x{z}_y+\frac{1}{n}\sum z_y^2& \ge 0\text{Note that}\frac{1}{n}\sum z^2=1\\ 1+2r_{xy}+1\ge 0& \\ 2+2r_{xy}\ge 0& \\ r_{xy}\ge -1& \end{array}$$

If we change the plus sign in eq. 3 into a minus sign, we get $r_{xy}\le 1$. In sum:

$$-1\le r_{xy}\le +1$$

Hence, we have found that the $r$ cannot exceed an absolute values of 1.