Wozu ist das gut?

Kurz gesagt ist die logistische Regression ein Werkzeug, um dichotome (zweiwertige) Ereignisse vorherzusagen (auf Basis eines Datensatzes mit einigen Prädiktoren).

Was sagt uns die logistische Regression?

Möchte man z.B. vorhersagen, ob eine E-Mail Spam ist oder nicht, so ist es nützlich, für jede zu prüfende Mail eine Wahrscheinlichkeit zu bekommen. So könnte uns die logistische Regression sagen: “Eine Mail mit diesen Ausprägungen in den Prädiktoren hat eine Wahrschenlichkeit von X Prozent, dass es sich um Spam handelt”.

Warum nicht die “normale” Regression?

Die “normale” Regression ist für so eine Situation nicht (gut) geeignet, da die normale Regression sowohl negative Werte als auch Werte über 1 (100%) vorhersagen kann - was für Wahrscheinlichkeiten keinen Sinn machen würde.

Beispiel bitte!

Nehmen wir den Datensatz Titanic als Beispiel-Datensatz. Die Forschungsfrage lautet:

Hat die Passagierklasse einen Einfluss auf die Überlebenswahrscheinlichkeit?

Vorbereitung: Daten und Pakete laden

library("titanic")
data("titanic_train")
library(mosaic)

Datensatz anschauen

inspect(titanic_train)

## 
## categorical variables:  
##       name     class levels   n missing
## 1     Name character    891 891       0
## 2      Sex character      2 891       0
## 3   Ticket character    681 891       0
## 4    Cabin character    148 891       0
## 5 Embarked character      4 891       0
##                                    distribution
## 1 Abbing, Mr. Anthony (0.1%) ...               
## 2 male (64.8%), female (35.2%)                 
## 3 1601 (0.8%), 347082 (0.8%) ...               
## 4  (77.1%), B96 B98 (0.4%) ...                 
## 5 S (72.3%), C (18.9%), Q (8.6%) ...           
## 
## quantitative variables:  
##             name   class  min       Q1   median    Q3      max        mean
## ...1 PassengerId integer 1.00 223.5000 446.0000 668.5 891.0000 446.0000000
## ...2    Survived integer 0.00   0.0000   0.0000   1.0   1.0000   0.3838384
## ...3      Pclass integer 1.00   2.0000   3.0000   3.0   3.0000   2.3086420
## ...4         Age numeric 0.42  20.1250  28.0000  38.0  80.0000  29.6991176
## ...5       SibSp integer 0.00   0.0000   0.0000   1.0   8.0000   0.5230079
## ...6       Parch integer 0.00   0.0000   0.0000   0.0   6.0000   0.3815937
## ...7        Fare numeric 0.00   7.9104  14.4542  31.0 512.3292  32.2042080
##               sd   n missing
## ...1 257.3538420 891       0
## ...2   0.4865925 891       0
## ...3   0.8360712 891       0
## ...4  14.5264973 714     177
## ...5   1.1027434 891       0
## ...6   0.8060572 891       0
## ...7  49.6934286 891       0

Aha! Etwa 38% der Menschen an Board haben überlebt.

Deskriptive Analyse

Ob die Überlebensrate (Wahrscheinlichkeit) von der Passagierklasse (pclass) abhängt? Schauen wir uns die Häufigkeitsunterschied an:

tally(~ Survived | Pclass, 
      data = titanic_train)

##         Pclass
## Survived   1   2   3
##        0  80  97 372
##        1 136  87 119

Besser in Anteilen:

tally(~ Survived | Pclass, 
      data = titanic_train,
      format = "proportion")

##         Pclass
## Survived         1         2         3
##        0 0.3703704 0.5271739 0.7576375
##        1 0.6296296 0.4728261 0.2423625

In der ersten Klasse lag die Überlebensrate bi ca. 63%, in der dritten nur noch bei 24%. Das ist ein großer Unterschied. Rein deskriptiv können wir unsere Forschungsfrage also bejaen, oder genauer, festhalten, dass die Daten diesen Schluss nahe legen.

Regressionsmodell spezifizieren

mein_glm1 <- glm(Survived ~ Pclass, 
                 data = titanic_train,
                 family = "binomial")

Ergebnisse betrachten

summary(mein_glm1)

## 
## Call:
## glm(formula = Survived ~ Pclass, family = "binomial", data = titanic_train)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.4390  -0.7569  -0.7569   0.9367   1.6673  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  1.44679    0.20743   6.975 3.06e-12 ***
## Pclass      -0.85011    0.08715  -9.755  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 1186.7  on 890  degrees of freedom
## Residual deviance: 1084.4  on 889  degrees of freedom
## AIC: 1088.4
## 
## Number of Fisher Scoring iterations: 4

Der Einfluss der Passagierklasse ist statistisch signifikant, das ist einfach zu sehen.

Überlebenswahrscheinlichkeit pro Klasse

Aber wo sieht man jetzt die Überlebenswahrscheinlichkeit pro Klasse? Vielleicht ist es so am einfachsten:

predict(mein_glm1, 
        newdata = data.frame(Pclass = c(1,2,3)),
        type = "response")

##         1         2         3 
## 0.6448970 0.4369809 0.2490789

Wir sagen R, dass sie auf Basis unseres Modells (mein_glm1) vorhersagen (predict) soll, wie die Überlebenswahrscheinlichkeit für eine Person der 1,2 und 3. Klasse ist. Mt type = "response" sagen wir R, dasss wir als Einheit die Skala der Response-Variablen (also Survived) haben wollen, das heißt, in Wahrscheinlichkeiten.

Die Wahrscheinlichkeit sind ziemlich genau die Werte, die uns die einfache deskriptive Analyse auch gezeigt hat, das macht Sinn.

Einflussgewicht des Prädiktors verstehen

Möchte man die Odds des Überlebens wissen, so muss man den in der R-Ausgabe angegebenen Wert delogarithmieren, also \(e^x\) rechnen, wobei \(x\) der Wert in der Ausgabe ist.

exp(-0.85)

## [1] 0.4274149

Die Einflussstärke des Prädiktors liegt also bei -.42 Odds. Von Passagierklasse 1 auf 2 (bzw. 2 auf 3) sinkt die Chance zu Überleben um 0.42. Grob gesagt sind das 0,5 oder 1/2. Liegt die Chance zu Überleben bei 1/2 bzw. 1:2, so heißt das, das 1 Person überlebt, und zwei sterben.

In Passagierklasse “Null” beträgt die Odds (die Chance) zu Überlgen:

exp(1.44679)

## [1] 4.249452

Also etwa 4:1, 4 überleben, 1 stirbt. Das ist hypothetisch, weil es gibt keine Passagierklasse Null. Schauen wir uns also die Chance für Klasse 1 an:

exp(1.45 - 0.42)

## [1] 2.801066

Etwa 2.8, grob gesagt: 3 überleben, 1 stirbt. Mit anderen Worten die Überlebenschance ist (etwas weniger als) 75%, wenn pclass = 1.

Visualisierung

plotModel(mein_glm1)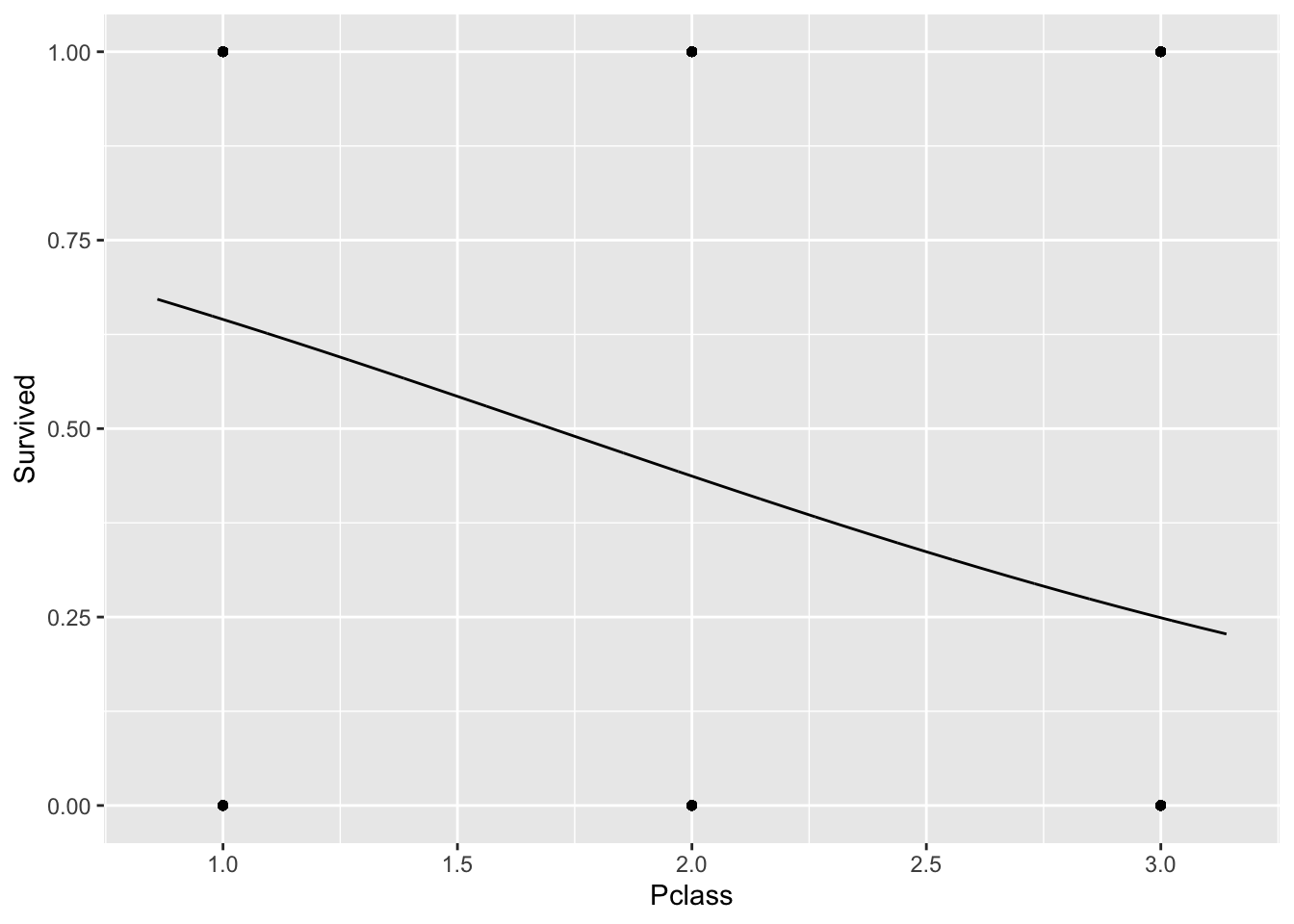

Hm, sieht man nicht so viel. Vielleicht nur den Scatterplot:

gf_jitter(Survived ~ Pclass, data = titanic_train, 
          width = .1, alpha = .3)

Oder mit Balkendiagrammen:

Zuerst die Häufigkeit in braver ("tidy), d.h. zum Visualisieren geeigneter Form:

tally(Survived ~ Pclass, format = "data.frame",
      data = titanic_train)

##   Survived Pclass Freq
## 1        0      1   80
## 2        1      1  136
## 3        0      2   97
## 4        1      2   87
## 5        0      3  372
## 6        1      3  119

Diese kleine Häufigkeitstabelle geben wir an gf_col (col wie Column) weiter.

tally(Survived ~ Pclass, 
      format = "data.frame",
      data = titanic_train) %>% 
  gf_col(Freq ~ Pclass, fill = ~ Survived,
         position = "fill")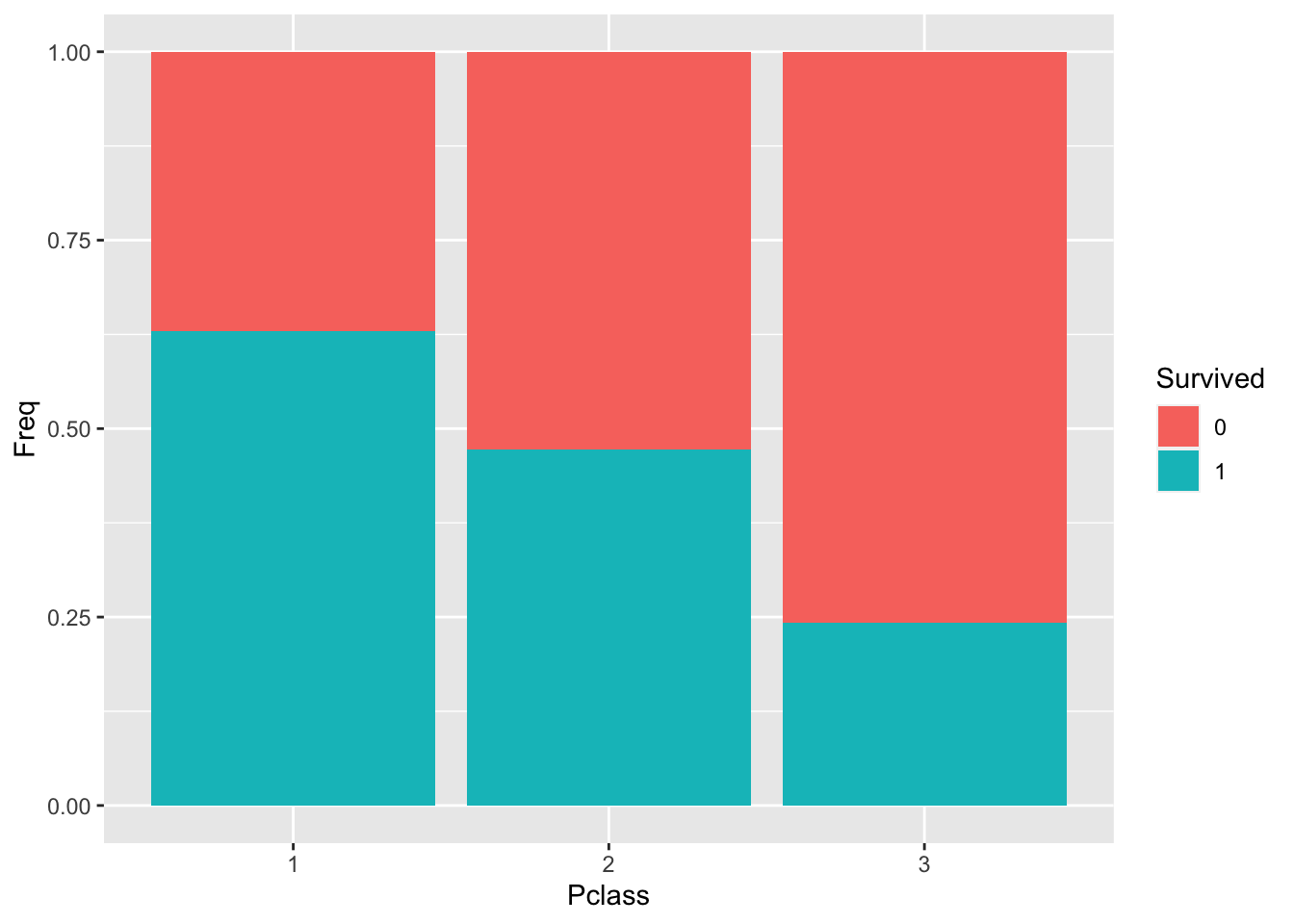

Klassifikationsgüte

Das Modell gibt uns für jeden Passagier die Überlebenswahrscheinlichkeit \(p\) zurück. Jetzt müssen wir uns noch entscheiden, welches Ereignis \(E\) wir der Wahrscheinlichkeit zuordnen. Die Ergebnismenge \(\Omega\) beinhaltet zwei Elemente: Überleben \(ü\) und sterben \(s\), \(\Omega = {ü, s}\) (oder wir könnten schreiben: \(\Omega = {1, 0}\). Die Frage ist also, bei welcher Wahrscheinlichkeit wir “überleben” und bei welcher “sterben” vorhersagen. Sagen wir, dass wir von “überleben” ausgehen, wenn das Modell eine Wahrscheinlichkeit größer 50% vorhersagt, andernfalls gehen wir von “sterben” aus:

\[ E= \begin{cases} {ü,} \mbox{ wenn } p > .5 \\ {s,} \mbox{ ansonsten } \end{cases} \]

Fügen wir als erstes die vorhergesagten Wahrscheinlichkeiten und das zugehörige Ereignis (ü, s) zum Datensatz hinzu. Es bietet sich an, überleben wird mit 1 und sterben mit 0 zu klassizieren.

titanic2 <- titanic_train %>% 
  mutate(Survived_p_est = predict(mein_glm1, 
                                  type = "response"),
         Survived_est = case_when(
           Survived_p_est > .5 ~ 1,
           Survived_p_est <= .5 ~ 0))

titanic2 %>% 
  select(Survived, 
         Pclass, 
         Survived_p_est, 
         Survived_est) %>% 
  head()

##   Survived Pclass Survived_p_est Survived_est
## 1        0      3      0.2490789            0
## 2        1      1      0.6448970            1
## 3        1      3      0.2490789            0
## 4        1      1      0.6448970            1
## 5        0      3      0.2490789            0
## 6        0      3      0.2490789            0

Das Suffix est steht für “estimated”, also für “vom Modell geschätzt”.

Jetzt vergleichen wir mal die tatsächlichen Ereignisse (ü,s) mit den Klassifikationen des Modells:

tally(~Survived | Survived_est, 
      data = titanic2)

##         Survived_est
## Survived   0   1
##        0 469  80
##        1 206 136

Die Gegenüberstellung von tatsächlichen und vom Modell vorhergesagten (klassifizierten) Ereignissen bezeichnet man auch als Konfusionsmatrix. Daraus lassen sich Gütekennzahlen ableiten. Einige wichitge sind:

Wie viele Personen (Fälle) wurden insgesamt korrekt klassifiziert? Gesamtgenauigkeit
Wie viele ü-Fälle wurden richtig (also als ü) klassifiziert? Sensitivität
Wie viele s-Fälle (Nicht-ü-Fälle) wurden richtig (also als s) klassifiziert? Spezifität

In diesem Fall gilt:

Gesamtgenauigkeit (accuracy)

a <- (469 + 136) / (469+80+206+136) 
a

## [1] 0.6790123

Komfortabler geht es mit einem mundgerechten Befehl, z.B. dem:

library(caret)

confusionMatrix(data = factor(titanic2$Survived_est), 
                reference = factor(titanic2$Survived))

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction   0   1
##          0 469 206
##          1  80 136
##                                           
##                Accuracy : 0.679           
##                  95% CI : (0.6472, 0.7096)
##     No Information Rate : 0.6162          
##     P-Value [Acc > NIR] : 5.536e-05       
##                                           
##                   Kappa : 0.2707          
##                                           
##  Mcnemar's Test P-Value : 1.453e-13       
##                                           
##             Sensitivity : 0.8543          
##             Specificity : 0.3977          
##          Pos Pred Value : 0.6948          
##          Neg Pred Value : 0.6296          
##              Prevalence : 0.6162          
##          Detection Rate : 0.5264          
##    Detection Prevalence : 0.7576          
##       Balanced Accuracy : 0.6260          
##                                           
##        'Positive' Class : 0               
##

Beispiel für eine logistische Regression