Daten
Sie arbeiten bei der Flughafenaufsicht von NYC. Cooler Job.
library(nycflights13)
data(flights)
Pakete laden
library(mosaic)
Stichprobe ziehen
Die Aufsichtsbehörde zieht eine Probe von 100 Flügen und ermittelt die “typische” Verspätung.
set.seed(42)
sample(flights$arr_delay, size = 100) -> flights_sample
Und berechnen wir die typischen Kennwerte:
favstats(~flights_sample, na.rm = TRUE)
#> min Q1 median Q3 max mean sd n missing
#> -51 -18.75 -5 11.75 150 0.4387755 31.1604 98 2
Ob $n=3$ ausreichen würde? Wäre billiger. “Fühlt” sich klein an…
set.seed(42)
sample(flights$arr_delay, size = 3) -> flights_small
favstats(~flights_small, na.rm = TRUE)
#> min Q1 median Q3 max mean sd n missing
#> -34 -28 -22 -0.5 21 -11.66667 28.91943 3 0
Hm, deutlich ungenauer.
Wie repräsentativ ist die Stichprobe?
Die Flughafenbetreiber beschweren sich. Die Stichprobe sei “nicht repräsentativ”; es sei “dumm gelaufen”.
Wie repräsentativ ist die Stichprobe? Keine Ahnung. Dazu müssten wir die Grundgesamtheit kennen. Die kennt man normalerweiß nicht.
In diesem Fall ausnahmsweise schon:
favstats(~arr_delay, data = flights, na.rm = TRUE)
#> min Q1 median Q3 max mean sd n missing
#> -86 -17 -5 14 1272 6.895377 44.63329 327346 9430
Median und MW der Sichprobe treffen die Wirklichkeit (Grundgesamtheit) “ganz gut”. Max und Min kaum.
Pech für die Flughafenbetreiber
Die Stichprobe entspricht der “typischen” Verspätung ganz gut. Ohne großes Aufsehen einigt man sich im Hinterzimmer. Kuh vom Eis.
Eine zweite, mysteriöse Stichprobe taucht auf
Die Presse bekommt eine weitere Stichprobe zugespielt: Mittlere Verspätung in NYC sei 42 Minuten ($n=100$)! Der Bürgermeister tobt. So lahm? Schlimmer als die Deutsche Bahn. Sie müssen schnell was tun. Nur was…
Ob die Stichprobe überhaupt echt ist?
Die zündende Idee
Sie ziehen viele vergleichbare Stichprobe aus der Grundgesamtheit (flights) und schauen, wie oft so ein Wert wie 42 als Mittelwert vorkommt!
Sagen wir, wir ziehen 10000 Stichproben und rechnen jeweils die mittlere Verspätung aus.
In wie vielen Stichproben ist die Verspätung 42 Minuten oder noch größer???
do(10000) * mean(sample(flights$arr_delay,
size = 100),
na.rm = TRUE) -> flights_vtlg
Schauen wir, wie oft 42 vorkommt:
gf_histogram(~mean, data = flights_vtlg)
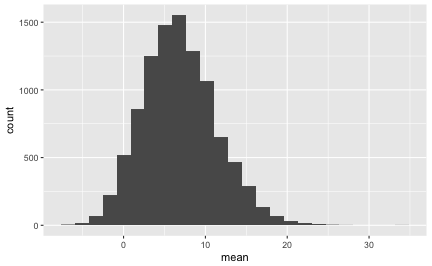
Praktisch nie! Fast keine Stichprobe hatte eine mittlere Verspätung von 42 Minuten.
Wir könenn mit hoher Sicherheit ausschließen, dass die Stichprobe echt ist! Der Bürgermeister überlegt öffentlich, Ihnen einen Orden zu verpassen (aber keine Gehaltserhöhung).
Das nennt man eine Stichprobenverteilung
Das Histogramm oben zeigt die Verteilung der 10000 Stichproben, die wir gerade gezogen haben (Danke, R). Man nennt es eine Stichprobenverteilung.
Die genauen Kennwerte dieser Stichprobenverteilung lauten:
favstats(~mean, data = flights_vtlg, na.rm = TRUE)
#> min Q1 median Q3 max mean sd n
#> -7.43299 3.677004 6.567716 9.721649 33.42105 6.850973 4.528796 10000
#> missing
#> 0
Die “typische” Stichprobe
Jetzt können wir genau sagen, wie die typische Stichprobe an New Yorker Verspätungne aussieht: Mittlere Verspätung: Etwa 7 Minuten (arith. Mittel); sd beträgt etwa 5 Minuten.
Die “ungewöhnlichen” Stichproben
Sagen wir, die 2.5% Stichproben mit der geringsten und die 2.5% Stichproben mit der höchsten Verspätung sind “ungewöhnlich”:
quantile(~mean, data= flights_vtlg,
probs = c(.025, .975))
#> 2.5% 97.5%
#> -1.234694 16.394142
Ah: Stichproben mit weniger als -1.24 Minuten und Stichproben mit mehr als 16 Minuten sind “ungewöhnlich”. Alles dazwischen ist “normal”.
In der Wirklichkeit ist die Grundgesamtheit unbekannt
Nettes Beispiel. Aber in Wirklichkeit haben wir praktisch nie die Grundgesamtheit, nur unsere einsame, einzige Stichprobe. Beispiele:
- Mittlerer Umsatz bei 30 Kunden: 42$. Umsatzpotenzial bei allen Deutschen? Unbekannt.
- Mittlere Anzahl von Handies in einer Stichprobe Ihrer Zielgruppe: 2.8 - Mittlere Anzahl Handies bei allen deutschen Jugendlichen? Unbekannt.
- Mittlere Zufriedenheit bei 100 befragten Nutzer: 4.2 von 5. Zufriedenheit aller Nutzer der Webseite? Unbekannt.
Die Grundgesamtheit ist in der Praxis oft unbekannt.
Durch einen Trick kann man die Grundgesamtheit schätzen
Der Trick lautet: Wir tun so, als sei unsere einzige Stichprobe die Grundgesamtheit. Dann machen wir weiter wie gerade: Wir ziehen viele Stichproben aus ihr.
Das nennt man Bootstrapping
Diese Idee nennt man Bootstrapping. Probieren wir es aus. Wichtig ist, immer mit Zurücklegen zu ziehen. Stellen Sie sich vor, jedes Element der Stichprobe kommt unendlich oft darin vor. Das ist ja die Idee einer Grundgesamtheit. Ziehen mit Zurücklegen ist die Umsetzung dieser Idee.
Mit resample geht das:
resample(flights_small)
#> [1] 21 21 21
resample(flights_sample)
#> [1] -26 -5 -41 -27 9 -16 13 27 -4 -8 3 7 4 20 -5 -19 21
#> [18] -20 25 -1 9 -1 -18 -20 -13 -21 -8 37 0 37 -13 -6 -8 -20
#> [35] -9 -28 -6 -39 -6 43 -19 32 -28 -29 -1 19 50 -3 -28 -28 -12
#> [52] -3 -5 3 8 -19 -41 32 27 -19 12 -16 -41 -13 -5 -22 -11 -9
#> [69] 27 -9 NA -21 25 20 -6 -34 25 -13 27 -6 -22 -5 -20 27 -34
#> [86] -5 -5 -1 -31 -26 5 0 7 -15 16 -16 -14 -1 -13 23
Was ist der Mittelwert?
mean(resample(flights_sample), na.rm = TRUE)
#> [1] -0.4343434
Kann man übrigens auch so schreiben:
resample(flights_sample) %>% mean(na.rm = TRUE)
#> [1] 0.43
Wir wiederholen diesen Schritt oft, sagen wir 10000 Mal:
flights_boot <- do(10000) * mean(resample(flights_sample), na.rm = TRUE)
Und schauen uns das Histogramm an:
#rename(flights_boot, arr_delay_avg = "mean") -> flights_boot
gf_histogram(~mean, data = flights_boot)
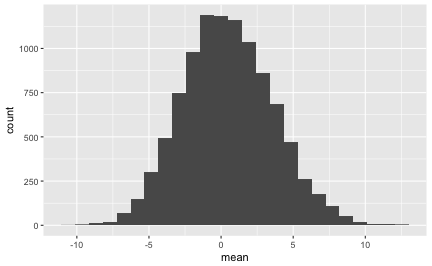
Die genauen Statistiken sehen so aus:
favstats(~mean, data = flights_boot, na.rm = TRUE)
#> min Q1 median Q3 max mean sd n
#> -10.36082 -1.693878 0.3787755 2.56701 12.81818 0.477432 3.127597 10000
#> missing
#> 0
Die Bootstrapping-Ergebnisse gleichen der Stichprobenverteilung
Hey, wie durch Zauberei haben wir mit unserer Bootstrap-Methode eine Verteilung erhalten, die der Stichprobenverteilung sehr ähnlich ist. Anhand der Bootstrap-Verteilung können wir jetzt sagen, was eine “typische” Stichprobe ist und ob die 42-Minuten-Stichprobe zu den ungewöhnlichen Stichproben gehört.
quantile(~mean, data= flights_boot, probs = c(.025, .975))
#> 2.5% 97.5%
#> -5.316582 6.909258
Stichproben mit mehr als 22 Minuten Verspätung gehören zu den “ungewöhnlihen” Stichproben; die 42-Minuten-Stichprobe ist also ungewöhnlich.
Ungewöhnlich könnte auch heißen - gefälscht
Wenn jemand sagt, heute (am 17. November) hätte es in Novisibirsk 27 Grad, dann wäre das “ungewöhnlich” für Novisibirsk und diese Jahreszeit. Oder: die Daten stammen nicht aus Novisibirsk (das ist freundlicher als zu sagen, sie seien gefälscht).
Die Flüge der 42-Minuten-Stichprobe stammen vermutlich nicht aus New York
So die Pressemitteilung, die der Bürgermeister schließlich herausgibt. Er lässt sich so zitieren: “42 Minuten Verspätung sind seehr ungewöhnlich für NYC. Daher sind diese Daten vermutlich gef… äh stammen nicht von unseren Flughäfen”.
Fazit
Mit der Bootverteilung kann man einschätzen, wie “typisch” eine Stichprobe für eine Grundgesamtheit ist. Außerdem kann man sagen, ob eine Stichprobe “ungewöhnlich” für eine Grundgesamtheit ist.