It is well-known that the notorious p-values is sensitive to sample size: The larger the sample, the more bound the p-value is to fall below the magic number of .05.
Of course, the p-value is also a function of the effect size, eg., the distance between two means and the respective variances. But still, the p-values tends to become significant in the face of larges samples, and non-significant otherwise.
Theoretically, quite simple and well understood. But let’s take the test of “real” data and do a simulation to demonstrate or test this behavior.
First, load some required packages
library(tidyverse)
Simulate data with large sample size
Next, we simulate data: A data frame of 20 cols and many rows (1e06, ie., 1 million). We should also make sure that the null hypothesis is false in our data. To that end, we let the mean values of the columns vary somewhat.
k <- 20
n <- 1e06
df <- data.frame(replicate(k,rnorm(n = n, mean = rnorm(1, 0, 1), sd = 1)))
Now let’s compute t-tests for each and every combination (cartesian product of all combinations). We will save the resulting p-values in a (square) matrix.
m <- matrix(nrow = k, ncol = k)
for (i in seq_len(ncol(df))) {
for (j in seq_len(ncol(df))) {
m[i, j] <- t.test(df[i], df[j])$p.value
}
}
One half of the matrix is redundant, as the matrix is symmetric. The same reasoning applies for the diagonal. Let’s take out the redundant elements.
m[lower.tri(m)] <- NA
m[diag(m)] <- NA
Let’s come up with a logical matrix indicating whether one cell (ie., one t-test) indicates a significant t-test (TRUE) or not (FALSE).
m_significant <- apply(m, c(1,2), function(x) x < .05)
Finally, let’s count the number of significant results, and sum then up.
m_significant %>% sum(TRUE, na.rm = TRUE)
## [1] 191
The number of different tests is $$(k*k - k)/2$$.
Which amounts, in this case to
(k*k-20)/2
## [1] 190
Hence, all tests are significant.
rm(df)
Simulate data with small sample size
Now, we repeat the same thing with a small sample.
simulate_ps <- function(n = 1e06, k = 20){
# arguments:
# n: number of rows
# k: number of columns
# returns: proportion of significant (p<.05) t-tests
set.seed(42)
# simulate data
df <- data.frame(replicate(k,rnorm(n = n, mean = rnorm(1, 0, 1), sd = 1)))
# matrix for t-test results
m <- matrix(nrow = k, ncol = k)
# cartesian product of all t-tests
for (i in seq_len(ncol(df))) {
for (j in seq_len(ncol(df))) {
m[i, j] <- t.test(df[i], df[j])$p.value
}
}
# take-out redundant cells
m[lower.tri(m)] <- NA
m[diag(m)] <- NA
# compute matrix to count number of significant t-tests
m_significant <- apply(m, c(1,2), function(x) x < .05)
# count
sum_significant <- m_significant %>% sum(TRUE, na.rm = TRUE)
sum_distinct_tests <- (k*k - k)/2
prop_significant <- sum_significant / sum_distinct_tests
rm(df)
return(prop_significant)
}
simulate_ps(n = 10, k = 20)
## [1] 0.5894737
Play around
Now, we can play around a bit.
ns <- c(5, 10, 15, 20, 30, 40, 50, 100, 200, 300, 500, 1000, 2000, 5000, 10000, 2e04, 5e04, 1e05)
ps <- vector(mode = "numeric", length = length(ns))
for (i in seq_along(ns)){
ps[i] <- simulate_ps(n = ns[i], k = 20)
print(ps[i])
}
## [1] 0.4263158
## [1] 0.5894737
## [1] 0.5789474
## [1] 0.7315789
## [1] 0.6473684
## [1] 0.7736842
## [1] 0.8368421
## [1] 0.8631579
## [1] 0.9473684
## [1] 0.8842105
## [1] 0.9157895
## [1] 0.9736842
## [1] 0.9894737
## [1] 0.9894737
## [1] 0.9947368
## [1] 0.9947368
## [1] 1
## [1] 0.9947368
Finally, let’s plot that:
data_frame(
ns = ns,
ps = ps
) %>%
ggplot +
aes(x = ns, y = ps) +
geom_line(color = "gray80") +
geom_point(color = "firebrick")
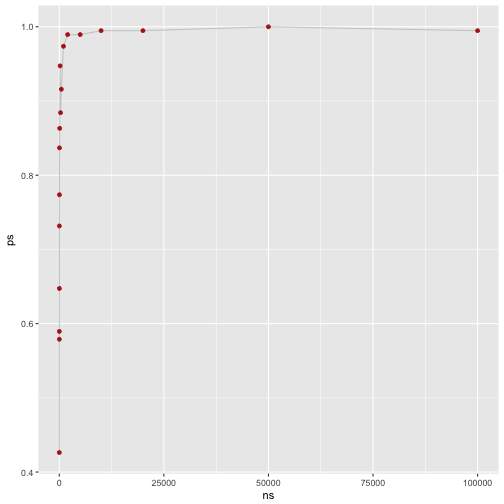
Thus, our result appears reasonable: The larger the sample size (ns), the higher the proportion of ps (ps).