Viele Menschen glauben an Horoskope. Doch warum? Ein Grund könnte sein, dass Horoskope einfach gut sind. Was heißt gut: Sie passen auf mich aber nicht auf andere Leute (mit anderen Strernzeichen) und sie sagen Dinge, die nützlich sind.
Ein anderer Grund könnte sein, dass sie uns schmeicheln und Gemeinplätze sind, denen jeder zustimmt: “Sie sind an sich ein Super-Typ, aber manchmal etwas ungeduldig” (oh ja, absolut, passt genau!). “Heute treffen Sie jemanden, der eine große Liebe werden könnte” (Hört sich gut an!). “Wenn Sie nicht aufpassen, könnte Ihnen heute ein Patzer unterlaufen” (Gut, dass ich gewarnt bin, ist nichts passiert heute, was beweisst, dass es richtig war, aufzupassen, Danke, Horoskop!).
Mit anderen Worten: Diese “Null-Hypothese” sagt, dass Horoskop ist so formuliert, dass man gerne zustimmt - unabhängig von den Inhalten. Die Studierenden in meinem Kurs wollten das überprüfen (das ist ein typischer Dozentensatz). Dafür haben wir uns folgende Studie überlegt: Wir legen unbedarften Versuchspersonen entweder ein echtes (vom Urheber des Horoskops als “wahr” erachtet) oder ein von uns gefälschtes Horoskop vor. Dann fragen wir, kurz gesagt: “Wie gut passt das Horoskop auf Dich?”.
Wenn das Horoskop nur Blabla ist, sollte das “Passungsgefühl” (wie gut das Horoskop auf die befragte Person passt) bei echten und gefälschten Horoskopen ungefähr gleich sein. Wenn die Horoskope die Menschen aber gut beschreiben sollten, dann sollten nur die Leute mit echten Horoskopen eine gute Passung berichten, nicht aber die Leute mit den gefälschten Horoskopen. Damit liegt die Hypothesen klar auf den Tisch – für uns, nicht für die Versuchspersonen, denen wir erstmal einen Bären aufbinden (müssen). Das nennt man dann “Coverstory” (klingt freundlicher und cooler).
In der Psychologie ist dieser Effekt als Barnumeffekt bekannt.
Schauen wir uns mal die Daten an.
Daten einlesen
Excel-Datei einlesen.
library(readxl)
data <- read_excel("~/Downloads/horo.xlsx")
Oder online die CSV-Datei einlesen.
data <- read.csv("https://sebastiansauer.github.io/data/horo.csv")
Erster Blick
library(dplyr)
glimpse(data)
## Observations: 54
## Variables: 6
## $ Sternzeichen <fctr> Zwilling, Skorpion, Skorpion, Steinbock, Waage...
## $ Wahnehmung <dbl> 0.00, 0.33, 0.33, 0.67, 0.67, 0.00, 0.33, 0.67,...
## $ Geschlecht <fctr> weiblich, männlich, männlich, weiblich, männli...
## $ Alter <int> 21, 27, 27, 26, 25, 26, 29, 26, 29, 30, 26, 33,...
## $ Gruppe <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,...
## $ Richtig_Falsch <fctr> F, F, F, F, F, F, F, F, F, R, R, R, R, R, R, R...
NAs loswerden
data %>%
filter(row_number() <= 44) -> data # ab Zeile 45 kommen nur noch Leerzeilen
# oder in der Excel-Datei die Zeilen (ab Z. 45) löschen
Check
Rechtschreibfehler bei “Wahnehmung”, das korrigieren wir.
rename(data, Wahrnehmung = Wahnehmung) -> data
Die Anzahl der “richtigen” und “falschen” Profilen sollte (etwa) gleich sein.
library(ggplot2)
data %>%
count(Richtig_Falsch)
## # A tibble: 2 × 2
## Richtig_Falsch n
## <fctr> <int>
## 1 F 20
## 2 R 24
qplot(x = Richtig_Falsch, data = data)
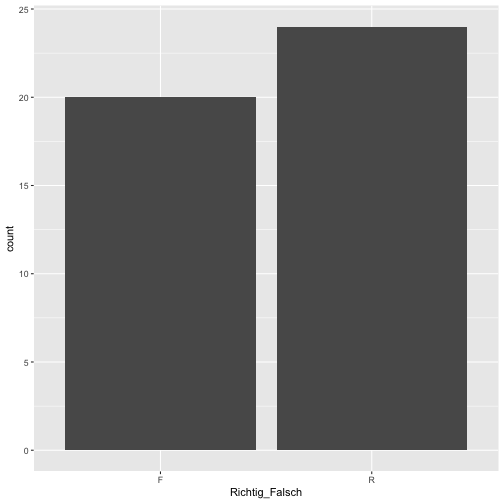 Ok, passt in etwa.
Ok, passt in etwa.
Schauen wir uns mal die Verteilung der Horoskope an.
qplot(x = Sternzeichen, data = data) + coord_flip()
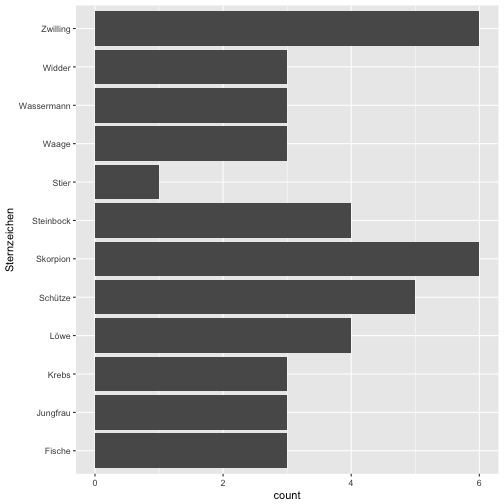
qplot(x = Sternzeichen, data = data, fill = Richtig_Falsch) + coord_flip()
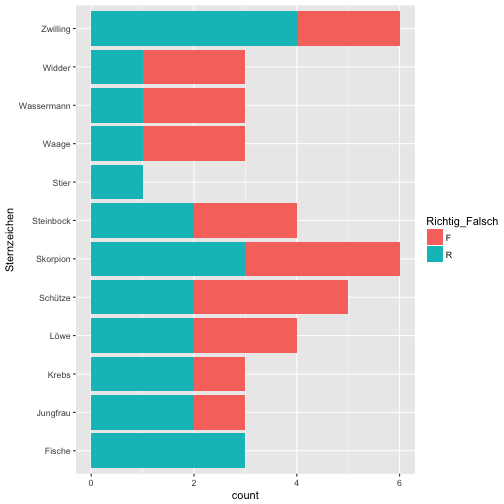
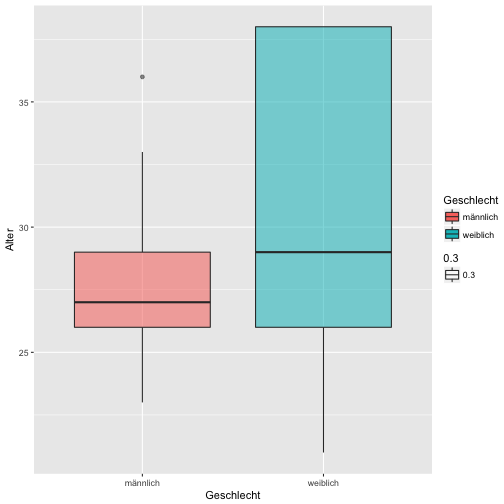
Spaßeshalber: Die Altersverteilung.
qplot(x = Geschlecht, data = data)
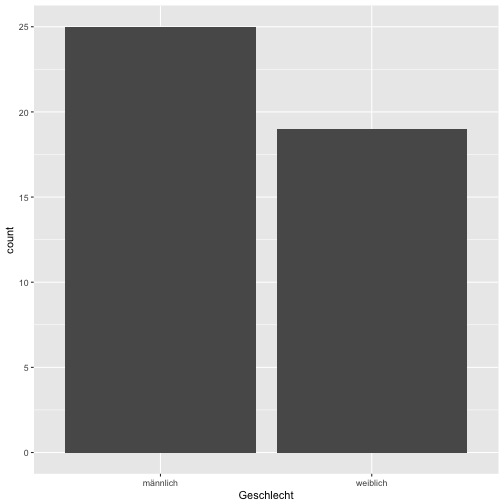
summary(data$Alter)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 21.00 26.00 27.00 28.56 29.75 38.00 26
qplot(y = Alter, x = Geschlecht, fill = Geschlecht, geom = "boxplot", data = data, alpha = .3)
## Warning: Removed 26 rows containing non-finite values (stat_boxplot).
“Wahrnehmung”
Ist die gefühlte Passgenauigkeit zwischen den beiden Gruppen gleich, so wie es der Barnum-Effekt vorhersagt?
Schauen wir mal…
data %>%
filter(!is.na(Wahrnehmung)) %>%
group_by(Richtig_Falsch) %>%
summarise(wahr_group_mean = mean(Wahrnehmung, na.rm = TRUE),
wahr_group_md = median(Wahrnehmung, na.rm = TRUE)) -> results1
results1
## # A tibble: 2 × 3
## Richtig_Falsch wahr_group_mean wahr_group_md
## <fctr> <dbl> <dbl>
## 1 F 0.5835000 0.670
## 2 R 0.4445833 0.415
Das plotten wir mal, ist ja so was wie ein zentrales Ergebnis.
results1 %>%
ggplot() +
aes(y = wahr_group_mean,
x = Richtig_Falsch) +
geom_bar(stat = "identity") +
xlab("Horoskop-Typ (Richtig vs. Falsch)") +
ylab("Gefühlte Passung des Horoskops")
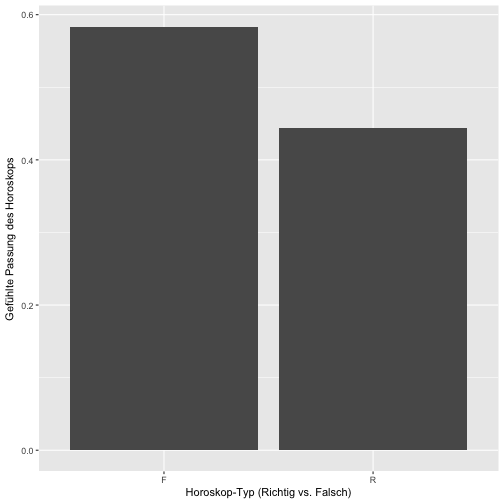
Eigentlich ist dieses Bild recht informationsarm. Schöner ist es (vielleicht) so:
data %>%
ggplot(aes(x = Richtig_Falsch, y = Wahrnehmung)) +
geom_boxplot() +
geom_jitter()
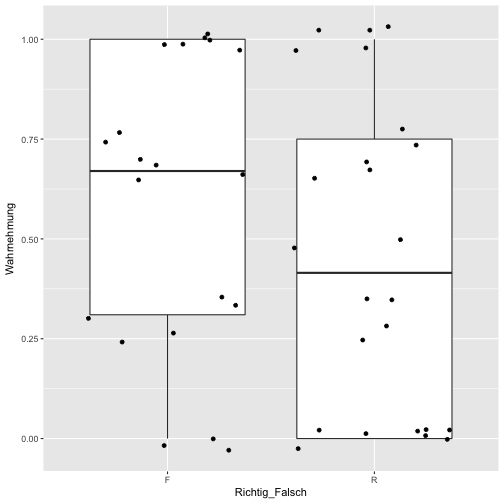
Hm, sieht etwas komisch aus. Vielleicht lieber ein Histogramm:
data %>%
ggplot(aes(x = factor(Wahrnehmung), fill = Richtig_Falsch)) +
geom_bar(position = "dodge")
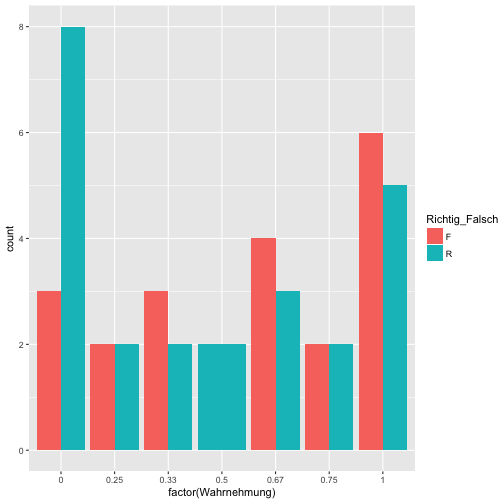
Das ist ganz aufschlussreich. Die Balken sind überall in etwa gleich hoch. Nur bei “Null-Passung” finden sich hauptsächlich echte Horoskope. Das spricht nicht für die Glaubhaftigkeit der Horoskope - und damit indirekt Unterstützung für den Barnum-Effekt.
Inferenzstatistik
Schauen wir mal ob sich die beiden Profilgruppen signifikant voneinander unterscheiden:
t.test(Wahrnehmung ~ Richtig_Falsch, data = data)
##
## Welch Two Sample t-test
##
## data: Wahrnehmung by Richtig_Falsch
## t = 1.2085, df = 41.436, p-value = 0.2337
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -0.09315257 0.37098591
## sample estimates:
## mean in group F mean in group R
## 0.5835000 0.4445833
Der p-Wert ist größer als .05, also nicht signifikant.
Effektstärke und Konfidenzintervall
Wie groß ist die Effektstärke des Unterschieds? Wie groß ist das Konfidenzintervall der Effektstärke?
data %>%
count(Richtig_Falsch)
## # A tibble: 2 × 2
## Richtig_Falsch n
## <fctr> <int>
## 1 F 20
## 2 R 24
library(compute.es)
tes(t = 1.21,n.1 = 20, n.2 = 24)
## Mean Differences ES:
##
## d [ 95 %CI] = 0.37 [ -0.25 , 0.98 ]
## var(d) = 0.09
## p-value(d) = 0.24
## U3(d) = 64.29 %
## CLES(d) = 60.22 %
## Cliff's Delta = 0.2
##
## g [ 95 %CI] = 0.36 [ -0.25 , 0.96 ]
## var(g) = 0.09
## p-value(g) = 0.24
## U3(g) = 64.05 %
## CLES(g) = 60.04 %
##
## Correlation ES:
##
## r [ 95 %CI] = 0.18 [ -0.13 , 0.46 ]
## var(r) = 0.02
## p-value(r) = 0.24
##
## z [ 95 %CI] = 0.19 [ -0.13 , 0.5 ]
## var(z) = 0.02
## p-value(z) = 0.24
##
## Odds Ratio ES:
##
## OR [ 95 %CI] = 1.94 [ 0.64 , 5.94 ]
## p-value(OR) = 0.24
##
## Log OR [ 95 %CI] = 0.66 [ -0.45 , 1.78 ]
## var(lOR) = 0.31
## p-value(Log OR) = 0.24
##
## Other:
##
## NNT = 8.53
## Total N = 44
Wie im Output steht:
d [ 95 %CI] = 0.37 [ -0.25 , 0.98 ]
Fazit
Die Daten sprechen nicht für die Glaubwürdigkeit der Horoskope; in beiden Gruppen (echt vs. gefakt) war die gefühlte Passung ählich. Wir fanden wenig Unterstützung für die Glaubwürdigkeit der Horoskope (bzw. dass die Leute die echten Horoskope glaubhafter einschätzten).
Der Signifikanztest war nicht signifikant; der Unterschied der Mittelwerte reichte nicht aus, um die H0 der Gleichheit zu verwerfen. Dieses Ergebnis kann auf die geringe Stichprobengröße zurückgeführt werden; andererseits kann es auch als Beleg für die Nullhypothese verstanden werden. Natürlich lassen die vorliegenden Daten keine starken Schlüsse zu; aber hey - es war eine schöne Übung :)
Die großen Effektstärkeintervalle sprechen dafür, dass der Effekt nur ungenau geschätzt wurde (aufgrund der geringen Stichprobengröße), was die Aussagekraft der Ergebnisse weiter abschwächt.
Witzigerweise war die mittlere subjektive Passung in der “gefälschten” Gruppe höher als in der “echten” Gruppe; dieser Effekt war von mittlerer Stärke (d = 0.37). Anschaulicher gesprochen: Zieht man eine Person aus jeder Gruppe, so ist die Wahrscheinlichkeit, dass die Person aus der “gefälschten” Gruppe ein größeres Passungsgefühlt hat, ca. 64% (bestenfalls).
Schluss, aus, Feierabend
Ok, für heute reichts :)