z-transformation is an ubiquitous operation in data analysis. It is often quite practical.
Example: Assume Dr Zack scored 42 points on a test (say, IQ). Average score is 40 in the relevant population, and SD is 1, let’s say. So Zack’s score is 2 points above average. 2 points equals to SDs in this example. We can thus safely infer that Zack is about 2 SDs above average (leaving measurement precision and other issues at side).
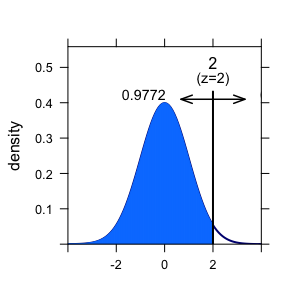
If the variable (IQ) is normally distributed, than we are allowed to look up the percentiles of this z-value in a table. Or ask the computer (in R):
pnorm(2)
## [1] 0.9772499
Here, R tells us that approx. 98% of all individuals have an IQ that is smaller than that of Dr. Zack. Lucky guy! Compare the figure.
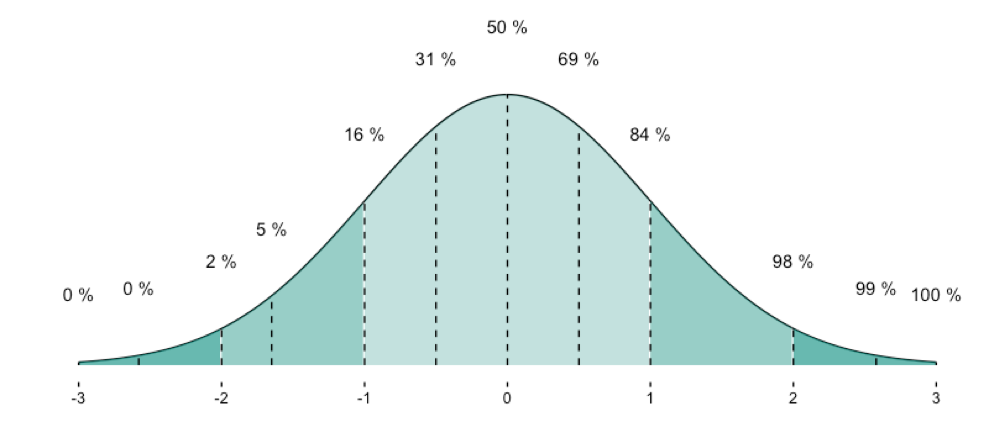
Here an overview on some frequently used quantiles of the normal distribution:
Now, next step. We have a bunch of guys, and test each of them. Say, 10 guys. Now we can calculate mean and SD of this distribution. To see the differences more clearly, we can z-transform the values.
IQ <- rnorm(10, mean = 40, sd = 1)
IQ
## [1] 40.91472 38.53260 40.30042 40.87957 40.99679 39.86815 40.14272
## [8] 39.26335 40.19174 39.85837
IQ_z <- scale(IQ)
IQ_z
## [,1]
## [1,] 1.05897590
## [2,] -2.01783361
## [3,] 0.26552871
## [4,] 1.01356631
## [5,] 1.16497561
## [6,] -0.29280567
## [7,] 0.06183789
## [8,] -1.07397171
## [9,] 0.12515803
## [10,] -0.30543146
## attr(,"scaled:center")
## [1] 40.09484
## attr(,"scaled:scale")
## [1] 0.7742196
Ok. Let’s compute mean and sd of the z-scaled values:
mean(IQ_z)
## [1] -4.605338e-15
sd(IQ_z)
## [1] 1
So it worked apparently.
But why is it that mean and sd will end up nicely with 0 (mean) and 1 (sd)?
To see this, consider the following. A z-transformation is in step 1 nothing more than subtracting the mean of some value. If I subtract the mean (42 here) from each value, and compute the mean then, I will not be surprised that the mean is now 42 points lower than it was. But 42-42=0. So the new mean (after z-transformation) will be 0.
Ok, but what about sd? Why must it equal 1? A similar reasoning applies. If I divide each value by the SD of the distribution (here 1), the new SD will be exactly by this factor lower. So whatever it used to be before z-transformtion, it will be 1 afterwards, as x / x = 1.